 |
Модуль 7. Аксонометрические проекции
|
|
|
|
Вопросы для самопроверки
1. Какие проекции называют аксонометрическими?
2. Назовите виды аксонометрических проекций.
3. Что называют коэффициентом (показателем) искажения?
4. Укажите натуральные и приведенные показатели искажения по направлениям осей в прямоугольной изометрии и диметрии.
5. Укажите направления и величины осей эллипсов изометрических и диметрических проекций окружности.
Примеры решения задач
Пример 59
По комплексному чертежу отрезка АВ построить его изображение в стандартной диметрии (рис.85).
Решение. Для построения изображения любой точки геометрической фигуры используется координатная ломанная линия с учетом коэффициентов искажения по аксонометрическим осям.
В начале строим аксонометрические оси x¢, y¢, z¢, которые пересекаются в точке O¢ и угол между x¢ и z¢ составит 97°10¢, между y¢ и z¢ - 131°25¢.
Аксонометрическая проекция точки (А¢) заданной точки А строим следующим образом. По оси x¢ откладываем натуральную величину координаты x точки А (Аx). Далее параллельно оси y проводим линию длиной 0.5 координаты y. Получаем вторичную горизонтальную проекцию (А¢1) точки А. Затем параллельно оси z¢ проводим линию, равную натуральной величине координаты z точки А. Таким образом получаем координатную ломанную О¢АxА¢1А¢.
Аналогичным образом получаем аксонометрическую проекцию (В¢) точки В.
Масштаб построения составит 1,06:1.

а) б)
Рисунок 85
Пример 60
Построить аксонометрическую проекцию пирамиды по заданным ортогональным проекциям (рис. 13.9).
Решение. Начинают с назначения координатных осей в ортогональных проекциях. Переход от ортогональных проекций к аксонометрическому изображению:
|
|
|
1) на ортогональном чертеже различают оси координат;
2) строят аксонометрическое оси;
3) по характерным точкам строят аксонометрическое изображение.
На рис. 9.3, б вначале построена вторичная проекция в пл. П2, а затем аксонометрическое изображение.

а) б)
Рисунок 86
Пример 61
Построить следы прямой l на аксонометрической проекции изображения (рис. 87).
Решение. Алгоритм решения задачи такой же, как и на эпюре Монжа. Продолжаем горизонтальную проекцию (l¢1) прямой до пересечения с осями x и y, где получаем точки Т¢1 и E¢1. Пересечение горизонтальной проекции (l¢1) прямой и аксонометрической проекции (l¢) дает точку К¢1. T – фронтальный след прямой l, K – горизонтальный след и E – профильный след.

Рисунок 87
Пример 62
Построить пересечение заданной прямой l и плоскости Г(АВС) (рис. 88).
Решение. Плоскость Г(АВС) и прямая l заданы своими аксонометрическими и вторичными проекциями. Задачу решаем, используя вспомогательную плоскость-посредник.
1. Заключаем прямую l во вспомогательную фронтальную плоскость S. При этом S¢1,совпадающая с l¢1, представляет собой вторичную проекцию вспомогательной плоскости. Отметим, что вторичная проекция любой фигуры, расположенной в плоскости S, совпадает с вторичной проекцией S¢1.
2. Строим пересечение заданной плоскости Г(АВС) с вспомогательной плоскостью S; во-первых находим точки пересечения вторичных проекций плоскостей (S¢1 пересекает A1¢B¢1C¢1 по линии 1¢12¢1); затем проводим вертикальные линии связи из 1¢1 и 2¢1 до пересечения с аксонометрическими проекциями соответствующих сторон заданной плоскости, а именно 1¢ и 2¢. Объединяем точки в прямую 1¢ 2¢.
3. Определяем точку Т¢ пересечения прямой l' и плоскости A¢B¢C¢, а именно l' пересекает 1¢2¢, при пересечении которых получаем точку Т¢. По принадлежности к l¢1, находим вторичную проекцию точки пересечения Т¢1.
|
|
|
4. Для определения видимости прямой относительно заданной плоскости воспользуемся конкурирующими точками 3 и 4, принадлежащими соответственно стороне ВС плоскости и заданной прямой. Проведя линии связи, определяем вторичные проекции выбранных точек. По положению вторичных проекций определяем видимость заданной прямой относительно плоскости.

Рисунок 88
Пример 63
Построить линии пересечения цилиндра и конуса плоскостью.
Решение. На рис. 89 и 90 показано построение в изометрической проекции линий пересечения цилиндра и конуса фронтально-проецирующими плоскостями. В рассматриваемых случаях линии пересечения представляют собой эллипсы.
Прежде всего, руководствуясь чертежом, наносим по координатам точек А' и С' линии наклона плоскостей a и b. Для построения точек эллипсов берем вспомогательные секущие плоскости: для цилиндра — параллельно его образующим и плоскости yOz, для конуса — проходящие через его вершину параллельно оси у. Эти плоскости задаются их следами, параллельными оси у, на плоскостях оснований цилиндра и конуса.
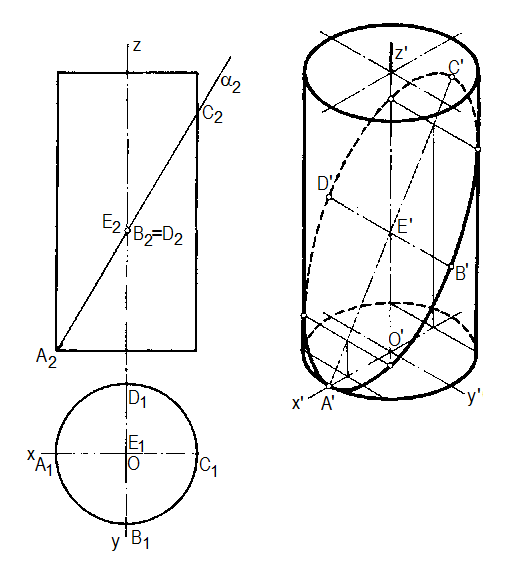
а) б)
Рисунок 89
При таком выборе вспомогательных плоскостей прямые, по которым они пересекаются с плоскостями a и b, получаются параллельными оси у. В пересечении этих прямых с образующими цилиндра и конуса получаются точки эллипса.
В первую очередь следует найти такие характерные точки, как отмеченные на чертежах буквами А, В, С и D, а также получаемые на очерковых линиях изометрической проекции. Малая полуось получаемого в сечении эллипса, равная CВ, сохраняет свою величину и в изометрической проекции (C¢B¢ =CB).

а) б)
Рисунок 90
Задачи по модулю 7
1. Построить три проекции и аксонометрию призмы с вырезом (рис. 91).
2. Построить три проекции и аксонометрию конуса с вырезом (рис. 92)
3. Построить три проекции и аксонометрию цилиндра с вырезом
4*. Построить три ортогональные проекции и аксонометрическую проекцию двух пересекающихся фигур: цилиндра и сферы.

Рисунок 91

Рисунок 92

Рисунок 93

Рисунок 92
|
|
|


