 |
Модуль 3. Проецирование плоскости
|
|
|
|
Вопросы для самопроверки
1) Какие способы задания плоскости на чертеже знаете?
2) Как найти следы плоскости?
3) Какое положение может занимать плоскость относительно плоскостей проекций?
4) Какие плоскости являются плоскостями частного положения?
5) Дайте определение плоскостей общего положения, проецирующих и уровня.
6) Какие линии называются главными линиями плоскости?
Примеры решения задач
Пример 12
Достроить вторую проекцию прямой l, принадлежащую плоскости ABC (рис. 21а).

а) б)
Рисунок 21
Решение: Построим горизонтальные проекции точек 1 и 2 (11 и 21 ) с помощью линий связи (см. рис. 21, б). Через точки 11 и 21 проведем горизонтальную проекцию прямой l.
Пример 13
В плоскости, заданной параллельными прямыми АВ и CD, провести произвольную прямую (рис. 22,а).
Решение. Задаемся на прямых (A1B1, А2В2) и (C1D1, C2D2) произвольными точками (M1, M2) и (N1, N2) и проводим через них прямую (M1N1, M2N2).
Пример 14
Дана плоскость пересекающимися прямыми АВ и CD. Определить, лежит ли прямая MN в этой плоскости (рис. 22,б).
Решение: Обозначаем точки пересечений фронтальных проекций прямых АВ и MN через К2 и прямых CD и MN через L2. Строим горизонтальные их проекции — точки К и L на горизонтальной проекции (M1N1) прямой MN. Из построения видно, что точки (K1, K2) и (L1, L2) прямой MN на заданной плоскости не лежат. Следовательно, прямая MN в плоскости не лежит. Решение этой задачи можно начать и с пересечений горизонтальных проекций — точек К и L.

а) б)
Рисунок 22
Пример 15
В плоскости, заданной двумя параллельными прямыми АВ и CD, провести фронталь на расстоянии 15 мм от фронтальной плоскости проекций (рис. 23).

Рисунок 23
Решение: Проводим на расстоянии 15 мм от оси проекций параллельную eй горизонтальную проекцию (M1N1) фронтали, которая пересекает прямые AB и CD в точках K и L. Затем находим точки K2 и L2 на прямых А2B2 и C2D2 и проводим через них фронтальную проекцию (M2N2) фронтали (дано одно решение).
|
|
|
Пример 16
В плоскости, заданной пересекающимися прямыми А В и CD, провести линию наибольшею ската (рис. 24).
Решение: Проводим произвольную горизонталь (M1N1, M2N2) плоскости. Так как линия наибольшего ската должна быть перпендикулярна этой горизонтали, проводим ее горизонтальную проекцию, например (Е1К1), перпендикулярно горизонтальной проекции (M1N1) горизонтали (теорема проектирования прямого угла), а затем по горизонтальной проекции (Е1К1) — линии наибольшего ската - находим ее фронтальную проекцию (E2K2).

Рисунок 24
Пример 17
Дана точка А и плоскость, заданная прямой DE и точкой С. Провести через точку А произвольную прямую параллельную заданной плоскости. (рис. 25)

Рисунок 25
Решение: Задаем в плоскости какую-нибудь прямую СК и через точку А проведем прямую АВ, проекции которой параллельны соответствующим проекциям прямой СК.
Пример 18
Даны фронтальный след (Р2) плоскости Р и точка А, лежащая на этой плоскости. Найти горизонтальный след (P1) плоскости (рис. 26).

Рисунок 26
Решение: Проводим через фронтальную проекцию (А2) точки фронтальную проекцию горизонтали плоскости Р — параллельно оси проекций, до пересечения с фронтальным следом (P2) плоскости в точке V (рис. 26). Найдя по точке V2 на оси проекций точку V1, проводим через точки A1 и V1 горизонтальную проекцию горизонтали, а параллельно ей - искомый горизонтальный след (P1) плоскости через точку Рх.
Пример 19
Дана точка А. Провести через нее плоскость Р, перпендикулярную к горизонтальной плоскости проекций и составляющую с фронтальной плоскостью проекций угол, равный 30° (рис. 27).
Решение. Угол между горизонтально-проецирующей плоскостью и фронтальной плоскостью проекций определяется углом между горизонтальным следом плоскости и осью проекций. Отсюда — проводим через горизонтальную проекцию (А1) точки горизонтальный след (Р1) плоскости под заданным углом 30° к оси проекции до пересечения с ней в точке Рx; затем проводим через точку Рx фронтальный след (Р2) плоскости перпендикулярно оси проекций. (Дано одно решение.)
|
|
|

Рисунок 27
Вывод. Если горизонтально-проецирующая плоскость проходит через точку, то горизонтальный след этой плоскости проходит через горизонтальную проекцию точки.
Пример 20
Построить следы плоскости Р общего положения, проходящей через точку А, зная точку схода следов (Рx) плоскости (рис. 28).
Решение. Используем фронталь плоскости. Проводим проекции произвольной фронтали через одноименные проекции заданной точки (А1,А2) и находим ее след (H1, H2). Проводим горизонтальный след (P1) плоскости через точки Рх и H1 и фронтальный след (P2) — через точку Рх — параллельно фронтальной проекции фронтали (почему?).
Примечание. Через точку А можно провести любую прямую.

Рисунок 28
Пример 21
Дан треугольник АВС и точка К. Определить расстояние от точки до плоскости.
Решение: Опускаем из точки К перпендикуляр на плоскость треугольника и находим точку – основание перпендикуляра. Определяем истинную величину отрезка перпендикуляра (рис. 29).
1) Для того, чтобы опустить перпендикуляр к плоскости, необходимо провести произвольно горизонталь и фронталь плоскости h и f. Затем проводим проекции перпендикуляра: горизонтальную – через проекцию K1 перпендикулярно горизонтальной проекции горизонтали (h1), и фронтальную – через проекцию K2 перпендикулярно фронтальной проекции фронтали (f2).
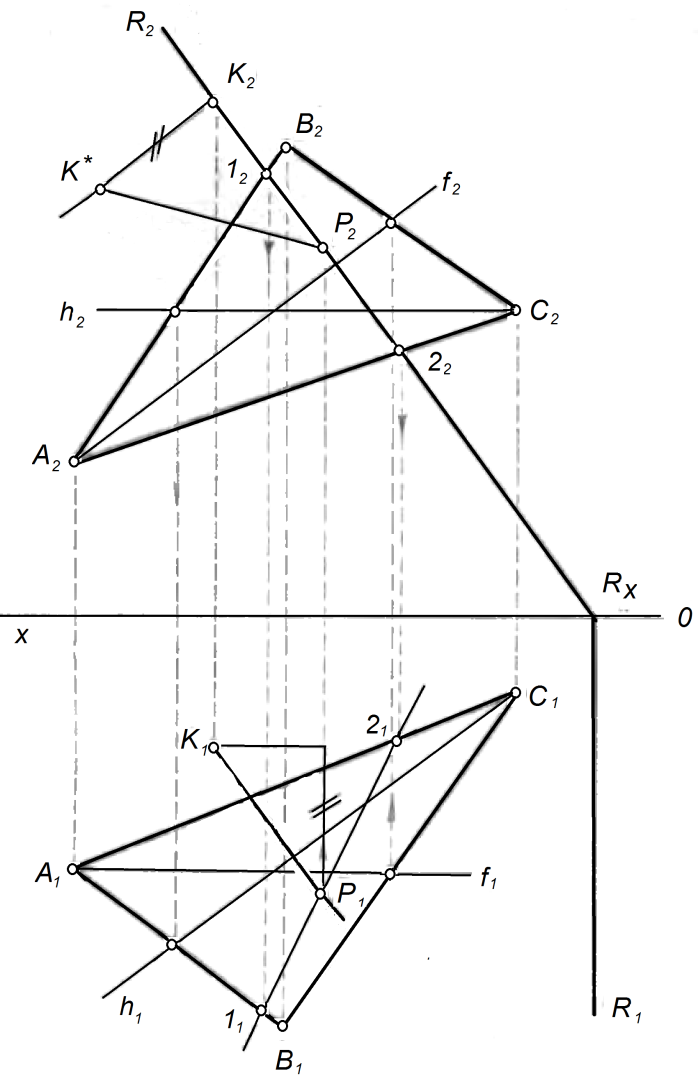
Рисунок 29
2) Для нахождения точки пересечения перпендикуляра и плоскости треугольника проведем фронтально-проецирующую плоскость R. Пересечение плоскости R и плоскости дает линию 12, с помощью которой мы находим искомую точку. Горизонтальная проекция линии 1121 пересекает горизонтальную проекцию перпендикуляра в точке Р1, что является горизонтальной проекцией основания перпендикуляра. Далее проецируем точку Р на фронтальную плоскость.
3) Найдем натуральную величину отрезка РК методом прямоугольного треугольника.K*P2 – натуральная величина расстояния от точки К до плоскости треугольника.
|
|
|
Пример 22
Построить линии пересечения двух плоскостей (поверхностей первого порядка), заданных треугольниками АВС и DEF, с использование плоскости уровня.
Решение: Линия пересечения двух плоскостей является прямой и, следовательно, определяется двумя различными точками (M и N), одновременно принадлежащими обеим плоскостям. В качестве вспомогательных поверхностей выбираются плоскости частного положения (проецирующие или плоскости уровня).
Проведем горизонтальную плоскость уровня α через точку А. При пересечении плоскостей α и АВС получаем линию 1А. При пересечении плоскостей α и DEF получаем линию 23.
Последовательность построения проекций следующая:
1) Построение фронтальной проекции плоскости уровня α (α2 – в виде горизонтальной линии на рис. 30).
2) Нахождение точек пересечения α2 и отрезков В2С2, D2F2, D2E2. Обозначаем соответственно точки 12, 32, 22. Получаем линии 2232 и 12А2.
3) Проецирование точек 1,2,3 на горизонтальную плоскость проекции. Обозначаем горизонтальные проекции - 11, 21, 31. Получаем линии 2131 и 11А1.

Рисунок 30
4) При пересечении 11А1, 2131 (линий пересечения плоскости уровня α и заданных плоскостей) получаем точку М1 – горизонтальную проекцию точки М.
Определение второй точки N, принадлежащей линии пересечения плоскостей, выполняется по аналогичному алгоритму. Прямая, соединяющая точки M и N, является искомой.
Пример 23
Построить линии пересечения двух плоскостей (поверхностей первого порядка), заданных треугольниками АВС и DEF, с использованием проецирующей плоскости.

Рисунок 31
Решение: Проведем фронтально-проецирующую плоскость α, при пересечение которой с отрезками АС и ВС дают линию пересечения плоскости α и плоскости АВС (проекции 1222). Так как линия DF и линия 12 лежат в одной плоскости, то при их пересечении получаем точку К (на горизонтальной плоскости проекций – точку К1).
Аналогичным образом найдена точка L – точка пересечения линии ВС и линии 34 с помощью горизонтально-проецирующей плоскости β.
|
|
|
Определение видимости проекций сторон треугольников, выполненное при помощи фронтально конкурирующих точек 1 и 6 и горизонтально конкурирующих точек 4 и 5, показано только на рис. 31.
Задачи по модулю 3
1. Задать произвольную горизонтально-проектирующую плоскость: 1) двумя пересекающимися прямыми; 2) прямой и точкой.

Рисунок 32

а) б)

в) г)
Рисунок 33
2. Задать плоскость, параллельную фронтальной плоскости проекций: 1) двумя параллельными прямыми; 2) тремя точками.
3. Задать произвольную фронтально-проектирующую плоскость: 1) двумя параллельными прямыми; 2) тремя точками.
4. Построить следы плоскости Р общего положения, проходящей через точку А (рис. 32).
5. Построить на заданной плоскости геометрическое место точек, удаленных от плоскости П1 на 15 мм (рис.33, а-г)
6*. Построить на плоскости Р точку А, лежащую в 1-ой, 2-ой и 3-ей четвертях (рис. 34, а-б).
7*. Перечислить прямые, которые можно провести в плоскости Р (рис. 35, а-г)

а) б)
Рисунок 34

а) б)

в) г)
Рисунок 35

а) б)
Рисунок 36

а) б)
Рисунок 37

а) б)
Рисунок 38
8*. Найти линию пересечения плоскостей Р и Q (рис. 36, а-б).
9*. Найти точку пересечения прямой АВ с плоскостью Р (рис. 37, а-б).
10**. Найти точку пересечения прямой АВ с заданными плоскостями (рис. 38, а-б).
11**. Найти линию пересечения плоскости, заданной двумя параллельными прямыми KL и MN, с плоскостью, заданной двумя пересекающимися прямыми АВ и АС, и указать, через какие четверти проходит искомая линия (рис. 39).

Рисунок 39
|
|
|


