 |
Анализ физических закономерностей формирования распределения случайных величин по значениям продолжительности проверки крепления стартера на автомобиле
|
|
|
|
Нормальное распределение.
Нормальное распределение, называемое также законом Гуса, находит широкое применение при исследовании эффективности функционирования транспортных средств и систем.
Теоретическим обоснованием широкого применения этого закона служит центральная предельная теорема (теорема Ляпунова А.М.), согласно которой распределение суммы независимых или слабо зависимых случайных величин, имеющих конечные математические ожидания и дисперсии одного порядка, при увеличении числа слагаемых всё меньше отличаются от нормального закона. При этом складываемые законы могут быть одинаковыми и разными.
Плотность распределения нормального закона имеет следующий вид:
,
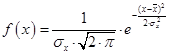где 
- математическое ожидание;
- среднее квадратичное отклонение.
Функция распределения нормального закона имеет вид:
Вероятность попадания в интервал a, b случайной величины, распределенной нормально, определяется с помощью табличной функции Лапласа Ф0:
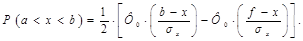
Логарифмически – нормальное распределение.
В этом случае нормальное распределение имеет не сама величина, а значение ее логарифма. Логарифмически-нормальное распределение формируется в случае, если на протекание исследуемого процесса и его результата влияет сравнительно большое число случайных и взаимно независимых величин, интенсивность действия которых зависит от достигнутого случайной величиной состояния.
Модель формирования называется моделью “пропорционального эффекта”. Данным законом хорошо описывать изменение геометрических, диагностических параметров, а так же для описания усталостных процессов, коррозии, наработки крепежных соединений.
|
|
|
В решении задач ТЭА Vx=0.3…0.7
Данное распределение описывает произведение воздействий случайных величин.
Дифференциальная функция логарифмически-нормального закона имеет вид:
где 
-случайная величина, логарифм которой распределен нормально;
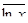-математическое ожидание логарифма случайной величины;
-среднее квадратическое отклонение логарифма случайной величины
Интегральная функция логарифмически-нормального распределения 
определяется следующим образом:
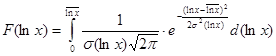
Расчет параметров математических моделей
Нормальное распределение
Нормальный закон формируется, если на протекание исследуемого процесса и его показателей влияет сравнительно большое число независимых или слабо зависимых элементарных факторов (слагаемых), каждый из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных.
Нормальный закон хорошо согласуется с результатами эксперимента по оценке параметров, характеризующих техническое состояние деталей, узла, агрегата и автомобиля в целом, а так же их ресурсов и наработки до появления первого отказа. Достаточно широкое распространение этого закона определяется тем, что рассматриваемые параметры формируются в реальных условиях эксплуатации под влиянием многочисленных взаимно независимых или слабо зависимых факторов. Интенсивность изнашивания и, следовательно, износ, ресурс детали зависит, например, от первоначальных свойств сопряженных деталей, смазочных материалов, условий работы, квалификации персонала, качества ТО, ремонта и т.д.
Для нормального закона распределения в задачах технической эксплуатации автомобилей коэффициент вариации 
Дифференциальная функция распределения
где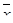 
- математическое ожидание;
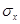- среднее квадратическое отклонение.
Интегральная функция распределения нормального закона:
|
|
|
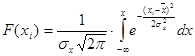
Вероятность попадания случайной величины, распределенной нормально в интервале определяется с помощью функции Лапласа (
)
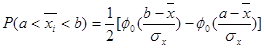
Заготавливаем статистическую таблицу
Таблица 2.2
Статистическая таблица для нормального распределения.
| Наименование параметра | Номер интервала | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1.Границы интервалов | 10,0; 11,5 | 11,5;13,0 | 13,0; 14,5 | 14,5; 16,0 | 16,0; 17,5 | 17,5; 19,0 | 19,0; 20,5 |
| 2.Середины интервалов | 10,75 | 12,25 | 13,75 | 15,25 | 16,75 | 18,25 | 19,75 |
| 3. Частота mi | 4 | 2 | 8 | 16 | 5 | 4 | 3 |
| 4.Опытные частоты попа- даний в интервалы | 0,095 | 0,048 | 0,19 | 0,381 | 0,119 | 0,095 | 0,071 |
| 5. Статистическая функция распределения F(xi)э | 0,095 | 0,143 | 0,333 | 0,714 | 0,833 | 0,929 | 1 |
| 6. Теоретические вероятности попадания в интервалы Pi | 0,046 | 0,117 | 0,2095 | 0,2505 | 0,117 | 0,1095 | 0,04 |
| 7. Теоретические числа попа- даний в интервалы m* | 1,932 | 4,914 | 8,799 | 10,521 | 4,914 | 4,599 | 1,68 |
| 8. Слагаемые критерия Пирсона | 0,455 | 0,013 | 0,854 | 0,567 | 0,177 | 0,01 | 0,016 |
| 9. Теоретическая функция распределения F(xi) | 0,046 | 0,163 | 0,3725 | 0,623 | 0,74 | 0,8495 | 0,89 |
Вычисляем общее статистическое математическое ожидание наработки:
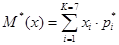
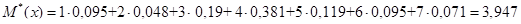
Вычисляем статистическую дисперсию:
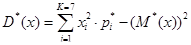
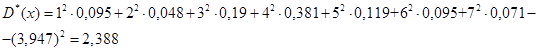
Несмещенное значение среднеквадратического отклонения:
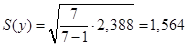
Выдвигаем гипотезу о нормальном распределении опытных данных.
Вычисляем с помощью табличной функции Лапласа теоретические вероятности попадания случайной величины в интервалы:
Для 1-го интервала
;
Для 2-го интервала
;
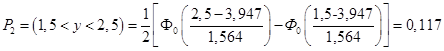Для 3-го интервала
;
Для 4-го интервала
;
Для 5-го интервала
;
Для 6-го интервала
;
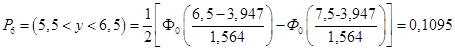Для 7-ого интервала
.
Значения теоретических вероятностей заносим в табл. 2.2 строка 5
На основании полученных теоретических вероятностей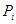 
производим сглаживание опытной гистограммы теоретической кривой нормального закона.
Находим теоретические числа попадания случайных точек в интервалы и записываем значения в табл. 2.2 строка 6.
;
;
;
;
;
;
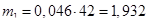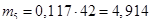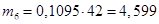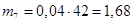
Вычисляем слагаемые критерия Пирсона, заполняя тем самым табл. 2.2 строка 7.
1-ый интервал 4-ый интервал
; 
;
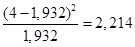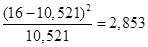2-ой интервал 5-ый интервал
; 
;
3-ий интервал 6-ой интервал
; 
;
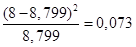7-ой интервал
|
|
|
.
Суммируя слагаемые критерия Пирсона по интервалам, получаем значение критерия Пирсона:
.
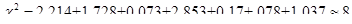Проверяем правдоподобность гипотезы о принадлежности опытных данных к нормальному закону с помощью критерия Пирсона:
-число степеней свободы равно
.
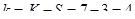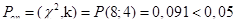-гипотеза не отвергается.
Проверяем правдоподобность гипотезы о принадлежности опытных данных к нормальному распределению с помощью критерия Романовского:
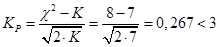
Таким образом, по критерию Романовского гипотеза не отвергается.
Расчет критерия Колмогорова.
В каждом из интервалов определяем модуль разности между экспериментальными значениями интегральной функции F(xi)э и теоретическими F(xi), т.е.
и выбираем максимальное значение Dmax. Вычисляем расчетное значение критерия:
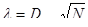
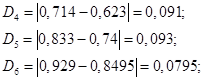
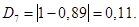
Таким образом, по критерию Колмогорова гипотеза не отвергается.
|
|
|
