Логарифмически-нормальной распределения

В этом случае нормальное распределение имеет не сама величина, а значение ее логарифма. Логарифмически-нормальное распределение формируется в случае, если на протекание исследуемого процесса и его результата влияет сравнительно большое число случайных и взаимно независимых величин, интенсивность действия которых зависит от достигнутого случайной величиной состояния.

Модель формирования называется моделью “пропорционального эффекта”. Данным законом хорошо описывать изменение геометрических, диагностических параметров, а так же для описания усталостных процессов, коррозии, наработки крепежных соединений.

В решении задач ТЭА Vx=0,3…0,7

Заготавливаем статистическую таблицу

Таблица 2.3

Статистическая таблица для логарифмически-нормального распределения.

Наименование параметра	Номер интервала
	1	2	3	4	5	6	7
1.Границы интервалов	10,0; 11,5	11,5;13,0	13,0; 14,5	14,5; 16,0	16,0; 17,5	17,5; 19,0	19,0; 20,5
2.Середины интервалов	10,75	12,25	13,75	15,25	16,75	18,25	19,75
3.Опытные числа попаданий в интервалы mi	4	2	8	16	5	4	3
4.Опытные частоты попаданий в интервалы	0,095	0,048	0,19	0,381	0,119	0,095	0,071
5. Натуральный логарифм для середины интервала	2,375	2,506	2,621	2,725	2,818	2,904	2,983
6. Центрированная и норми- рованная случайная величина	1,793	1,082	0,457	0,109	0,614	1,082	1,511
7. Плотность нормированной и центрированной случайной величины	0,080	0,222	0,359	0,391	0,330	0,222	0,127
8. Плотности распределения f(xi)	0,04	0,098	0,142	0,139	0,107	0,066	0,035
9. Теоретические числа попаданий в интервалы mi*	2,52	6,174	8,946	8,779	6,741	4,158	2,205
10. Слагаемые критерия Пирсона	0,869	2,822	0,1	5,939	0,449	0,006	0,287
11. Вероятности не попадания в интервалы	0,94	0,853	0,787	0,791	0,839	0,901	0,947
12. Теоретические вероятности попадания в интервалы Pi	0,06	0,147	0,213	0,209	0,161	0,099	0,053
13. Теоретическая функция распределения F(xi)	0,06	0,207	0,42	0,629	0,79	0,889	0,942
14.Экспериментальные значения интегральной функции F(xi)э	0,095	0,143	0,333	0,714	0,833	0,929	1

 

Выдвигаем гипотезу о возможности распределения по логарифмически-нормальному закону.

Вычисляем значения натуральных логарифмов для середины интервалов:

 

 

 

 

 

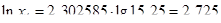
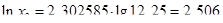
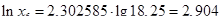
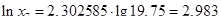
Вычисляем статистическое математическое ожидание и дисперсию случайной величины:

 

 

 

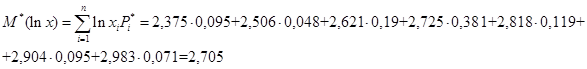
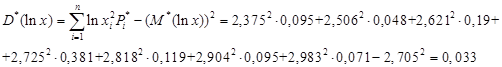
Несмещенная оценка для дисперсии :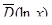

 

 

 

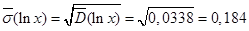
Вычисляем центрированные и нормированные значения случайной величины и заносим значения в таблицу 2.3 строка 6.

 

 

 

 

 

 

 

 

 

 

 

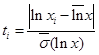
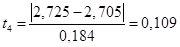
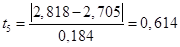
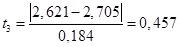
Находим плотности распределения для центрированных и нормированных случайных величин, используя таблицу:

 

 

 

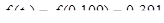
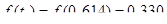
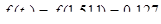
Заносим данные в таблицу 2.3 строка 7

Вычисляем плотности распределения случайной величины, заполняем строку 8 табл. 2.3

 

 

 

 

 

 

 

 

 

 

 

 

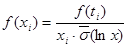
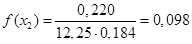
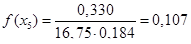
Вычисляем теоретические вероятности попадания случайной величины  в интервал по формуле:

 

 

 

 

 

 

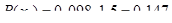
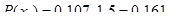
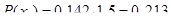
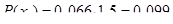
Заполняем строку 12 табл.2.3

Вычисляем теоретические числа попадания случайной величины в интервалы по формуле: и заполняем строку 9 табл.2.3

 

 

 

 

 

 

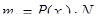
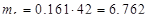
Вычисляем составляющие критерия Пирсона для каждого интервала и заполняем строку 10 табл. 2.3

 

 

 

 

 

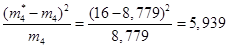
Суммируя слагаемые критерия Пирсона по интервалам, получаем значение критерия Пирсона:

 

 

Проверяем правдоподобность гипотезы о принадлежности опытных данных к логарифмически-нормальному закону.

По критерию Пирсона:

 

 

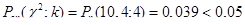
Следовательно, по критерию Пирсона гипотеза о принадлежности опытных данных к логарифмически-нормальному закону отвергается.

По критерию Романовского:

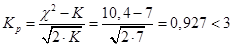 - гипотеза не отвергается

 

Вычисляем вероятности исправной работы (кривая ресурса), для этого суммируем плотности распределения

 

 

 

 

 

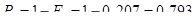
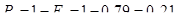
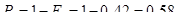
Расчет критерия Колмогорова.

В каждом из интервалов определяем модуль разности между экспериментальными значениями интегральной функции F(xi)э и теоретическими F(xi), т.е.

 

 

и выбираем максимальное значение Dmax. Вычисляем расчетное значение критерия:

 

 

 

 

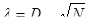
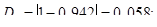
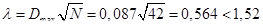
Таким образом, по критерию Колмогорова гипотеза не отвергается.

 

12345

Поделиться:

Воспользуйтесь поиском по сайту: