 |
Порядок выполнения лабораторной работы
|
|
|
|
А.П. МИТРОФАНОВ
«ОПТИМИЗАЦИЯ ИНЖЕНЕРНЫХ
РЕШЕНИЙ»
министерство образования и науки российской федерации
Волжский политехнический институт (филиал)
ФЕДЕРАЛЬНОГО государственного БЮДЖЕТНОГО образовательного учреждения высшего образования
«волгоградский государственный технический университет»
А.П. Митрофанов
«ОПТИМИЗАЦИЯ ИНЖЕНЕРНЫХ РЕШЕНИЙ»
Учебно-методическое пособие

Волгоград
УДК 621.91.01
Рецензенты:
Доктор физико-математических наук, чл.-кор. РАЕ, профессор, заведующий кафедрой «Общая физика» филиала ФГБОУ ВО «Национальный исследовательский университет «МЭИ» в г. Волжском В.Г. Кульков;
кандидат технических наук, доцент кафедры «Общественное
питание, процессы и оборудование перерабатывающих производств» ФГБОУ ВО «Волгоградский государственный аграрный университет»
Н.И. Лебедь
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Митрофанов, А.П. Оптимизация инженерных решений [Электронный ресурс]:учебно-методическое пособие/ А.П. Митрофанов//Сборник «Учебные пособия». Выпуск 3.-Электрон.текстовые дан.(1 файл-2,23MБ) – Волгоград: ВПИ (филиал) ВолгГТУ, 2016 г. – Систем.требования: Windows 95и выше; ПК с процессором486+;CD-ROM.
Учебно-методическое пособие содержит материалы практических занятий при изучении курса «Оптимизация технологических процессов». Материал пособия подобран с учетом разносторонности требуемых знаний, достаточно подробно рассматриваются приемы и методы оптимизации различных практических инженерных задач.
Предназначено для студентов высших учебных заведений, обучающихся по направлению подготовки 27.03.01 «Стандартизация и сертификация» и может использоваться при изучении курса для всех форм обучения.
|
|
|
Ил. 32, табл. 31, библиограф. 8 назв.
| Ó Волгоградский государственный технический университет, 2016 Ó Волжский политехнический институт, 2016 |
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ……………………………………………………… | |
| Работа 1. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ……………………………….. | |
| Работа 2. РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАМ-МИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ………………………………. | |
| Работа 3. ЗАДАЧА КОММИВОЯЖЕРА (МЕТОД ВЕТВЕЙ И ГРАНИЦ)…………………………………………………………………… | |
| Работа 4. ТРАНСПОРТНАЯ ЗАДАЧА……………………………. | |
| Работа 5. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ……………. | |
| Работа 6. ПЛАНИРОВАНИЕ РАБОЧЕЙ СИЛЫ ……………….. | |
| Работа 7. ОПТИМИЗАЦИЯ ЗАМЕНЫ ОБОРУДОВАНИЯ НА ПРЕДПРИЯТИИ…………………………………………………………… | |
| Работа 8. ЗАДАЧИ УПОРЯДОЧЕВАНИЯ (АЛГОРИТМ ДЖОНСА)………………………………………………………………….. | |
| СПИСОК ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ…………………… |
ВВЕДЕНИЕ
В настоящее время теория оптимизации, успешному применению которой способствует современная компьютерная техника, вносит заметный вклад в ускорение научно - технического прогресса. Трудно назвать такую область инженерной деятельности, где ни возникали бы задачи оптимизационного характера. Это, например, задачи определения наиболее эффективного режима работы различных технических систем, задачи на составление смесей при наименьших затратах сырья, задачи организации производства, дающего наибольшую возможную прибыль при заданных ограниченных ресурсах и др.
Курс «Оптимизация инженерных решений» рассчитан на аудиторию, подготовленную по математике в пределах программы технического вуза. Постановка каждой задачи оптимизации включает два объекта: множество допустимых решений и целевую функцию (функционал), которую следует минимизировать или максимизировать на указанном множестве. С этой точки зрения и рассматриваются различные классы экстремальных задач, составляющие предмет изучения линейного, динамического, нелинейного, геометрического программирования, вариационного исчисления и теории оптимального управления.
|
|
|
Остановимся на двух направлениях: линейном и нелинейном программировании. Здесь решаются задачи оптимизации, в которых целевая функция - эта функция многих переменных, а допустимым множеством решений является подмножество евклидова пространства.
РАБОТА №1. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Цель работы — знакомство с теорией по данной теме и применение ее в решении прикладных задач.
Теоретическое введение
Графический метод основан на геометрической интерпретации задачи
линейного программирования (ЗЛП) и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства. Задачу пространства размерности больше трех измерений изобразить графически вообще невозможно.
Пусть ЗЛП задана в двумерном пространстве, т. е. ограничения содержат две переменные.
| Z = C1X1 + C2X2 (1.1) |
Найти минимальное значение функции
при ограничениях
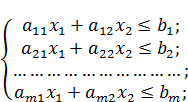 (1.2)
(1.2)
 (1.3)
(1.3)
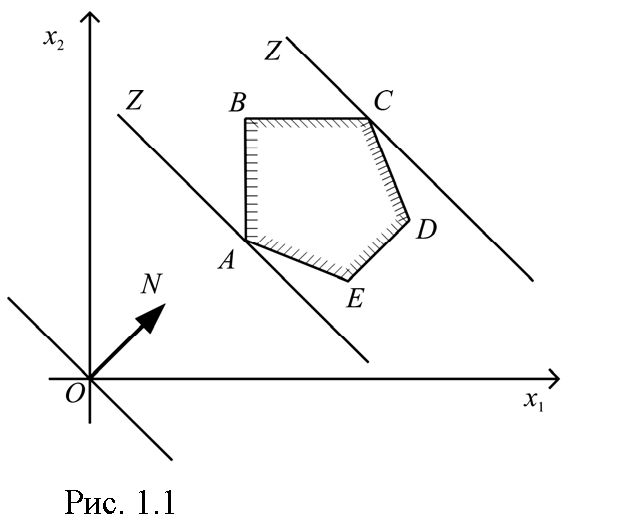
| Рис.1.1 |
 , где
, где  иx1 = 0, x2 = 0.
иx1 = 0, x2 = 0.
Линейная функция (1.1) при фиксированном значении Zявляется уравнениемпрямой: C1X1 + C2X2 = const.
Построим многоугольник решенийсистемы (1.2), (1.3) и график линейнойфункции (1.1) приZ=O(рис. 1.1). ТогдапоставленнойЗЛП можно датьследующую интерпретацию. Найти точку многоугольника решений, в которой прямаяC1X1 + C2X2= constопорная и функция Z при этом достигает минимума.
Значения Z возрастают в направлении вектора N = (C1, C2), поэтому прямую Z = 0 передвигаемпараллельно самой себе в направлении вектора N.
Из рис. 1.1 видно, что прямая Z = const дважды становится опорной в точке A и C, что соответствует минимуму в точке A и максимуму в точке C. Координаты точки A (x 1; x 2) находим, решая систему уравнений для прямых ABи AE. Если многоугольник решений представляет неограниченную многоугольную область, то возможны два случая:
|
|
|
1) прямая Z = const, передвигаясь в направлении N или противоположномему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной; значит линейная функция не ограничена на многоугольникерешений как сверху, так и снизу (рис. 1.2, а);
2) прямая Z = const, передвигаясь все же становится опорной. Тогда в зависимости от вида области линейная функция может быть ограничена только сверху (рис. 1.2, б), только снизу (рис. 1.2, в) или сверху и снизу (рис. 1.2,г). 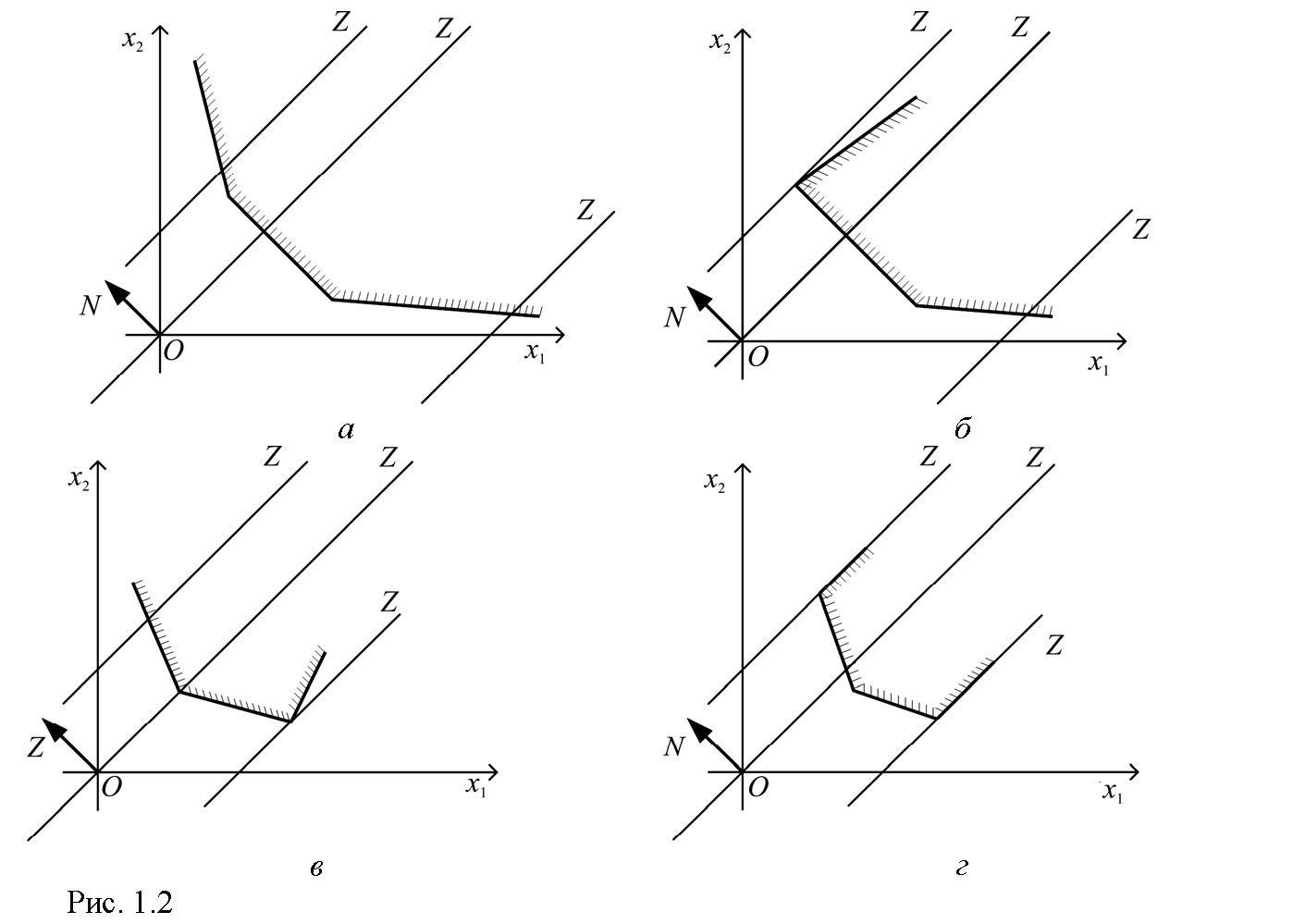
Рис. 1.2
Вообще, с помощью графического метода может быть решена ЗЛП, система ограничений которой содержит n неизвестных и m независимых уравнений, если n и m связаны соотношением n – m = 2.
Порядок выполнения лабораторной работы
1. Составить математическую модель задачи.
2. Построить многоугольник решений в системе координат x 1 Ox 2.
3. Построить радиус-вектор и прямую Z = 0, проходящую через точку
O (0; 0) перпендикулярно.
4. Провести прямые, параллельные прямой Z = 0, опорные по отношениюкмногоугольнику решений.
5. Найти оптимальные планы и значения Z minи Z max.
Примеры выполнения лабораторной работы
Пример 1.Для изготовления двух видов продукции P1 и P2 используют
три вида сырья: S1, S2, S3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, записаны в постановке ЗЛП.
x 1 – количество единиц продукции P1; х 2 –количество единиц продукции P2;Z – функции цели (максимальная прибыль).
1. Математическая модель задачи. Найти максимум функции Z =50 х 1+ 40 х 2 при ограничениях


2. 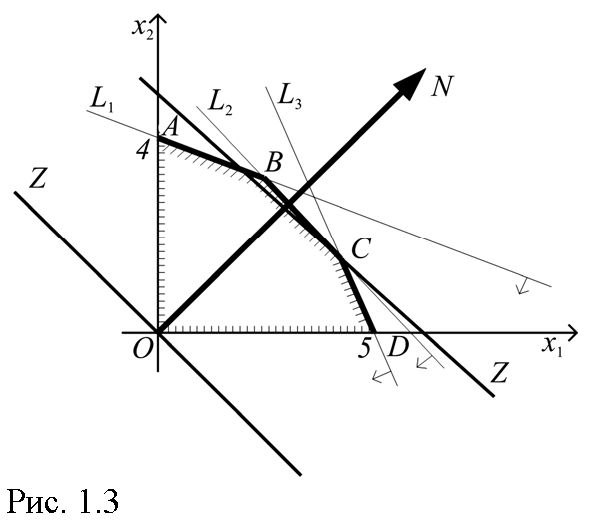
| Рис. 1.3 |


Взяв какую-нибудь точку, например, О(0; 0),установим, какую полуплоскость определяетсоответствующее неравенство.
|
|
|
Многоугольником решений данной задачи является ограниченныйпятиугольник OABCD.
3. Для построения прямой 50 x 1 + 40 x 2 = = 0 строим радиус-вектор Л (50; 40) = 10(5; 4) и через точкуО проводим прямую, перпендикулярную Л.
4. ПостроеннуюZ = 0 перемещаем параллельно самой себе в направлениивектора Л. Из рис. 1.3 видно, что опорной прямаяZ = constстановится в точке С, где Zпринимает максимальное значение.
5. ТочкаС лежит на пересечении прямыхL2и L3. Для определения ее координат решаем систему уравнений:

Оптимальный план задачи: x 1≈ 3,9; x 2≈ 1,7.
Подставляя x 1и x 2в Z, получаем Z max≈ 260,3.
Таким образом, чтобы получить максимальную прибыль необходимо запланировать производство 3,9 единиц продукции P 1и 1,7 продукции P 2.
Пример 2. Графическим методом найти оптимальный план ЗЛП, при которой линейная функция Z = 2 x 1– x 2 + x 3–3 x 4 + 4 x 5 достигает максимального значения при ограничения
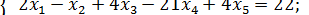

Используя метод Жордана–Гаусса, произведем три полных исключениянеизвестных х1 х2, х3. В результате приходим к системе
 (1.4)
(1.4)
Откуда x 1 = 6– x 4 + 3 x 5; x 2 = 70 –7 x 4–10 x 5; x 3 = 20 + 4 x 4–5 x 5. (1.5)
Подставляя эти значения в линейную функцию и отбрасывая в системе (1.4) базисные переменные, получаем задачу, выраженную только через свободные неизвестные х4 и х5; найти максимальное значение функции
Z = 6 x 4 +15 x 5–38 при ограничениях


Построим многогранник решений и линейную функцию в системе координат х 4 Ох 5 (рис. 1.4).
 Рис. 1.4
Рис. 1.4
|
Из рис. 1.4 заключаем, что линейная функция принимает максимальное значение в угловой точке B, которая лежит на пересечении прямых2и 3. В результате решения системы

находим х 4= 2, х 5= 28/5.
Максимальное значение функции Zmax = − 38 + 12 + 84 = 58.
Для отыскания оптимального плана исходной задачи подставляем в формулу (1.6) найденные значения х 4 и х 5. Окончательно получаем х 1= 104/5; х 2= 0; х 3= 0; х 4= 2; х 5= 28/5.
Требования к отчету
Отчет должен содержать:
1) титульный лист;
2) условие задачи;
3) чертеж с графической иллюстрацией решения задачи, пояснения
к чертежу;
4) все промежуточные окончательные вычисления;
5) вывод и анализ полученных результатов.
Варианты индивидуальных заданий
Найти минимум и максимум целевой функции при заданных ограничениях.
| Вариант 1. | Z = x 1 + 5 x 2


| Вариант 2. | Z = 5 x 1 + 3 x 2


|
| Вариант 3. | Z = 3 x 1 + 2 x 2


| Вариант 4. | Z = 4 x 1 + 3 x 2


|
| Вариант 5. | Z = 6,5 x 1 – 7,5 x 3 + 23,5 x 4 – 5 x 5

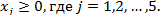
| Вариант 6. | Z = 5 x 1 + x 2


|
| Вариант 7. | Z = 6 x 1 + x 2


| Вариант 8. | Z = x 1 + 7 x 2


|
| Вариант 9. | Z = x 1 + 8 x 2


| Вариант 10. | Z = – x 1+4 x 2 + 2 x 4 – x 5

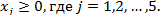
|
| Вариант 11. | Z = x 1+ x 2
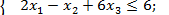

| Вариант 12. | Z = 3 x 1 + x 2


|
| Вариант 13. | Z = x 1 + x 2


| Вариант 14. | Z = x 1+2 x 3+ x 5

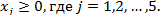
|
| Вариант 15. | Z = x 1 + 3 x 2


| Вариант 16. | Z = 2 x 1 + 3 x 2


|
| Вариант 17. | Z = 7 x 1 + 3 x 2


| Вариант 18. | Z = 2 x 1 + 3 x 2


|
| Вариант 19. | Z = x 1 + x 2


| Вариант 20. | Z = – 5 x 1+ x 2 – x 3

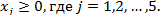
|
| Вариант 21. | Z = – 16 x 1 – x 2 + x 3+ 5 x 4+ 5 x 5

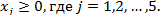
| Вариант 22. | Z = 3 x 1 + 4 x 2


|
|
|
|
Контрольные вопросы
1. На чем основан графический метод решения задачи линейного программирования?
2. Какие задачи линейного программирования можно решать графическим методом?
3. Каким может быть многоугольник решений?
4. Что геометрически означает каждое неравенство в системе ограничений?
РАБОТА №2. РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ
Цель работы — усвоение симплекс-метода и приобретение практических навыков его применения.
Программное обеспечение: табличный процессор MicrosoftExcel.
Теоретическое введение
Решение любой ЗЛП можно найти либо симплексным методом, либо методом искусственного базиса. Прежде чем применять один из методов, нужно ЗЛП записать в канонической форме.
Идея симплексного метода. Симплексный метод основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает или убывает (при условии, что заданная ЗЛП имеет оптимальныйплан и каждый ее опорный план является невырожденным). Переход возможен, если известен какой-нибудь опорный план.
Количество опорных планов определяется числом C^. При больших nи mнайти оптимальный план, перебирая все опорные планы, трудно. Поэтому
необходимо иметь схему, по которой осуществляется упорядоченный переход от одного опорного плана к другому. Такой схемой является симплексный метод решения ЗЛП.
Пусть дана ЗЛП.
Найти минимальное значение функции
 (2.1)
(2.1)
при ограничениях
 (2.2)
(2.2)
 (2.3)
(2.3)
Здесь aij, bjиCj 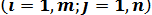 – заданныепостоянные числа
– заданныепостоянные числа
(m < n и bi>0).
Векторная форма данной задачи имеет следующий вид.
Найти максимум функции
 (2.4)
(2.4)
Приусловиях
x1A1 + x2A2+... + xmAm+... + xnAn = A0';(2.5)
 (2.6)
(2.6)

Таккак b1A1 + b2 A2 +... + bmAm = A0, то по определению опорного плана
X = (b1; b2;...; 0;...;0)является опорным планом данной задачи (последние n- mкомпонент вектора Xравны 0). Этот план определяется системой единичных векторов A1, A2,..., Am, а также вектор A0 могут быть представлены в виде линейной комбинации векторов данного базиса.
Пусть 
Положим 
Так как векторы A1, A2,..., Amединичные, то  и
и  ,атакже
,атакже  .
.
Т е о р е м а 2.1. Опорный план X*=(x1*; x2*;…xm*;0;…;0) задач (2.4)—(2.6)является оптимальным, если  для любого
для любого  .
.
Теорема 2.2. Если ∆k<0 для некоторого j = kи среди чисел aik≤0(i=1,m) нет положительных aik<0, то целевая функция(2.4)задачи—(2.6) не ограничена на множестве ее планов.
Т е о р е м а 2.3. Если опорный план Х задачи (2.4)—(2.6) не вырожден и ∆k <0, но среди чисел aikесть положительные (не все aik<0), то существует опорный план X' такой, что Z(X') >Z(X).
Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность, а также дальнейший
вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать в симплексную таблицу.
Порядок выполнения работы
1. Составить математическую модель задачи.
2. Решить ЗЛП симплекс-методом, используя для расчетов ТП Excel. Алгоритм метода включает следующие этапы:
1) найти первоначальный опорный план;
2) составить симплекс-таблицу, используя для расчетов ТП Excel;
3) выяснить, имеется ли хотя бы одно положительное (при минимуме) или отрицательное (при максимуме) число ∆j; если нет, то найденный опорный план оптимален; если же среди чисел ∆jимеются положительные (отрицательные), то либо установить неразрешимость задачи, либо перейти к новому опорному плану;
4) найти направляющие столбец и строку; направляющий столбец определяется наибольшим по абсолютной величине числом ∆j, а направляющая строка — минимальным из отношений компонентов столбца A0к положительным компонентам направляющего столбца;
5) используя метод Жордана — Гаусса исключения неизвестных, сделать новый базисный вектор Ajединичным; при этом определить компоненты нового опорного плана, коэффициенты разложения векторов Ajпо векторам нового базиса и числа Z' и ∆j '; все эти числа записать в новой симплекс-таблице;
6) проверить найденный опорный план на оптимальность; если план не оптимален и необходимо перейти к новому опорному плану, то снова нужно искать разрешающий элемент и далее по алгоритму, а в случае получения оптимального плана или установления неразрешимости процесс решения закончить.
3. Проверить полученный результат с помощью инструментального средства Solver(Решатель) ТП Excel (Сервис/Поиск решения).
Пример выполнения работы
Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл. 2.1.
| Вид сырья | Нормы затрат на одно изделие, кг. рат сырья на одно изделие, кг | Общее кол-ва сырья, кг | ||
| А | В | С | ||
| Цена | — |
Таблица 2.1
Изделия А, В и С могут производиться в любых соотношениях (сбыт
обеспечен), но производство ограничено выделенным предприятию сырьемкаждого вида. Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Решение
Составим математическую модель задачи. Искомый выпуск изделийАобозначим через X 1, изделий В— через х 2, изделийС — через х 3. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные x 1, х 2, х 3 должны удовлетворять следующей системе неравенств:
 (2.7)
(2.7)
Общая стоимость произведенной предприятием продукции при условии выпуска X 1изделий А, х 2 изделий В и х 3 изделий С составляет
F = 9x1 + 10x2 + 16x3. (2.8)
По своему экономическому содержанию переменные x1, х2 и х3 могут
принимать только лишь неотрицательные значения: x1, х2, х3>0.
Таким образом, приходим к следующей математической задаче: среди
всех неотрицательных решений системы неравенств (2.7) требуется найти такое, при котором функция (2.8) принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам.Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений:

Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, х4 — это неиспользуемое количество сырья 1-го вида.
Преобразованную систему уравнений запишем в векторной форме:
х 1 Р 1 + х 2 Р 2 + х 3 Р 3 + х 4 Р 4 + х 5 Р 5 + х 6 Р 6= Р 0.
где  ,
,  ,
,  ,
, 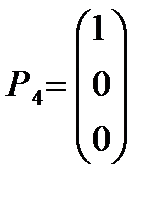 ,
,  ,
,  ,
,  .
.
Поскольку среди векторов P 1, P 2, P 3, P 4, P 5, P 6имеются три единичных
вектора, для данной задачи можно непосредственно записать опорный план.
Таковым является план Х= (0, 0, 0, 360, 192, 180), определяемый системой
трехмерных единичных векторов P 4, P 5, P 6, которые образуют базис трехмерного векторного пространства.Составляем симплексную таблицу для 1-й итерации (табл. 2.2), подсчитываем значения F0, Zj- Cjи проверяем исходный опорный план на оптимальность:
F0 = (C, P 0) = 0; Z 1 = (C,P) = 0; z 2 = (C, P 2); Z 3 = (C, P,) = 0;
z1-c1=0-9 =-9; z2-c2=0-10=-10; z3-c3=-16.
Для векторов базиса zj- cj = 0.
Таблица 2.2
| i | Базис | Cj | Pc | 9 | 10 | 16 | 0 | 0 | 0 |
| Р1 | Р2 | Р3 | Р4 | Р5 | P6 | ||||
| 1 | Р4 | 0 | 360 | 18 | 15 | 12 | 1 | 0 | 0 |
| 2 | Р5 | 0 | 192 | 6 | 4 | 8 | 0 | 1 | 0 |
| 3 | Р6 | 0 | 180 | 5 | 3 | 3 | 0 | 0 | 1 |
| 4 | — | — | 0 | -9 | -10 | -16 | 0 | 0 | 0 |
Этот план не оптимален, так как в 4-й строке имеется три отрицательных числа: z1-c1=-9; z2-c2=-10; z3-c3=-16. На основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число ∆jстоит в 4-й строке столбца P 3, то в базис введемвектор P3.
Определяем вектор, подлежащий исключению из базиса. Для этого находимθ0 = min (bi/ai1) для ai1> 0. т.е. θ0= min (360/12; 192/8; 180/3) = 192 /8 = 24. Следовательно, вектор P5подлежит исключению из базиса. Столбец вектора P3и2-ястрока являются направляющими.
Составляем табл. 2.3 для 2-й итерации, используя вычислительные возможности ТП Exсel (ввод формульных данных с абсолютными и относительными адресами, копирование формул, форматирование числовых данных).
Таблица 2.3
| i | базис | Cb | Р0 | ||||||
| Р 1 | P 2 | Р 3 | P 4 | P 5 | P6 | ||||
| Р 4 | —1,50 | ||||||||
| Р 3 | 0,75 | 0,5 | 0,125 | ||||||
| Р 6 | 2,75 | 1,50 | 0,00 | 0,00 | -0,38 | ||||
| — | — | -2 |
Найденный на 2-й итерации план задачи не является оптимальным и необходимо повторить все действия.
В табл. 2.4 в 4-й оценочной строке все числа неотрицательные. Это означает, что найденный опорный план является оптимальным и Fmax= 400.
Таблица 2.4
| i | Базис | Cb | Р0 | ||||||
| Р 1 | Р 2 | Р 3 | Р 4 | Р 5 | Р 6 | ||||
| Р 2 | 0,111 | – 0,166 | |||||||
| Р 3 | 0,25 | –0,055 | 0,208 | ||||||
| Р 6 | 1,25 | –0,166 | –0,125 | ||||||
| — | — | 0,222 | 1,666 |
Проверим шаги вычисления пользуясь командой ТП ExcelСервис/Поискрешения.Введем необходимые данные и ограничения следующим образом (рис. 2.1).
 Рис. 2.1
Рис. 2.1
|
Выберем команды Сервис/Поиск Решения. Заполним окно диалога Поиск решения (рис. 2.2).
 Рис. 2.2
Рис. 2.2
|
Установим параметры в окне Параметры поиска решения (рис. 2.3). После командыВыполнить откроется окно диалога Результаты поиска решения, которое сообщить что решение найдено (рис.2.4).

Рис. 2.3

Рис. 2.4
Оптимальный план и максимальное значение целевой функции появятся в соответствующих ячейках таблицы (рис. 2.5).

Рис. 2.5
Требования к отчету
Отчет должен содержать:
1. титульный лист;
2. описание всех этапов выполнения лабораторной работы с необходимыми формулами, таблицами, рисунками;
3. анализ полученных результатов и вывод.
Варианты индивидуальных заданий:
Вариант 1—10. Задача об использовании ресурсов.Для изготовления n видов продукции P 1, …, P n предприятие использует m видов ресурсов S 1, …, S m (сырье, топливо, материалы и т.д.). Запасы ресурсов каждого вида ограничены и равны b 1, …, b m. На изготовление единицы продукции j -го вида (j = 1, …, n) расходуется a ij единиц i -го ресурса (i = 1,…, n). При реализации единицы j -ой продукции предприятие получает C j единиц прибыли. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль(табл. 2.5).
Таблица2.5
| Вариант | Виды ресурсов | Расход ресурсов на единицу продукции | Запасы ресурсов | Доходы от реализации единицы продукции | ||||||
| P1 | P2 | P3 | CP1 | CP2 | CP3 | |||||
| S1 | ||||||||||
| S2 | ||||||||||
| S3 | ||||||||||
| S4 | ||||||||||
| S1 | — | — | ||||||||
| S2 | — | |||||||||
| S3 | — | |||||||||
| S4 | ||||||||||
| S1 | — | — | ||||||||
| S2 | — | |||||||||
| S3 | — | |||||||||
| S1 | — | — | ||||||||
| S2 | — | |||||||||
| S3 | — | |||||||||
| S4 | — | |||||||||
| S1 | 150 000 | |||||||||
| S2 | 170 000 | |||||||||
| S3 | 100 000 | |||||||||
| S4 | ||||||||||
| S1 | ||||||||||
| S2 | ||||||||||
| S3 | ||||||||||
| S1 | 0,6 | 0,4 | 0,6 | |||||||
| S2 | 0,2 | 0,4 | 0,3 | |||||||
| S3 | 0,2 | 0,6 | 0,4 | |||||||
| S1 | 0,6 | 0,5 | 0,4 | |||||||
| S2 | 0,7 | 0,4 | 0,8 | |||||||
| S3 | 0,3 | 0,2 | 0,5 | |||||||
| S1 | ||||||||||
| S2 | ||||||||||
| S3 | ||||||||||
| S1 | ||||||||||
| S2 | 0,3 | 0,2 | 0,3 | |||||||
| S3 | ||||||||||
Вариант 11—15. Задача о загрузке оборудования (1-го типа). Предприятие выпускает nвидов изделий P 1,..., Pnкаждое из которых проходит последовательную обработку на станках типов T1,..., Tm.Запас мощности станков, т.е. рабочее время станка, составляет соответственно b1,..., bmединиц времени. Изделие Piобрабатывается первым станком (типа
T1) ai1единиц времени, вторым станком — ai2единиц времени и т.д. При реализации одно изделие Piприносит прибыли Ciединиц прибыли, где i = 1,..., n. Составить такой план загрузки станков, при котором предприятие получит максимальную прибыль (табл. 2.6).
Таблица 2.6
| Вариант | Типы станков | Продолжительность обработки изделия на станке | Доход от реализации изделий | Запас мощности станков | ||||
| P1 | P 2 | P3 | CP1 | CP2 | CP3 | |||
| T1 | 13 200 | |||||||
| T2 | 24 000 | |||||||
| T3 | ||||||||
| T1 | — | — | ||||||
| T2 | — | |||||||
| T3 | — | |||||||
| T4 | — | |||||||
| T1 | ||||||||
| T2 | ||||||||
| T3 | ||||||||
| T1 | — | — | ||||||
| T2 | — | |||||||
| T3 | — | |||||||
| T1 | — | — | ||||||
| T2 | — | |||||||
| T3 | — |
|
|
|


