 |
Матрица стоимости возврата
|
|
|
|
| Узел | ||||||
| ∞ | ∞ | |||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ |
| Все 48<маршруты<73 |
| 3.5 |
| 6,3 |
| 6,3 |
| 2,4 |
| 2,4 |
| 3,5 |
| 2,1 |
| 5,6 |
| 3.5 |
| 4,3 |
| 4,3 |
| 6,2 |
| ∞ |
| 1,4 |
| 2,1 |
| 5,6 |
Рисунок 3.3 Оптимальное решение
С новой матрицей, матрицей стоимости возврата, выполняют описанные процедуры ветвления и построения границ. Полученное при этом дерево изображено на рисунке 3.3. Нахождение верхних границ не обязательно, но эта операция иногда позволяет сократить производимые вычисления. Из рис. 3.3 следует, что нижняя граница даже неполного маршрута, не содержащего звено (1, 4), превышает 63. Таким образом, маршрут, содержащий звено (1, 4), является оптимальным. Оптимальный маршрут состоит из следующих звеньев или пар пунктов: (6, 2); (4, 3); (3, 5); (5, 6); (2, 1); (1, 4). Он является ориентированным циклом, стоимость проезда по которому равна 63, т.е. 630 условных денежных единиц.
Задача коммивояжера не может быть непосредственно сформулирована и решена как задача линейного программирования. Основная ее особенность заключается в том, что в ней требуется существование ориентированного цикла, в который ровно один раз входят все узлы сети.
Для решения задачи коммивояжера можно использовать табличный процессор MicrosoftExcel. На рис.3.4 приведено решение задачи коммивояжера в табличном процессоре MCExcel с помощью инструментального средства Поиск решения.
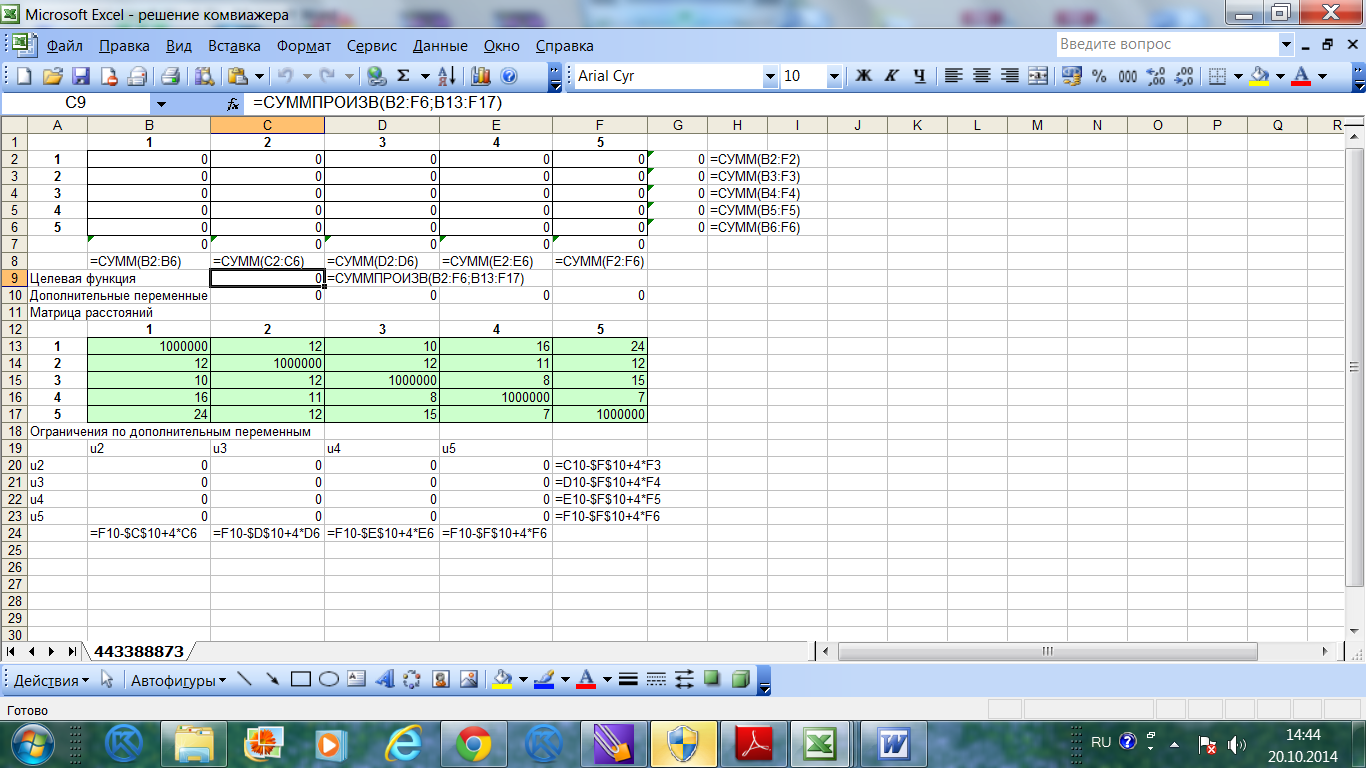
Рис. 3.4
Последовательность решения:
|
|
|
Заполнить таблицу с исходными данными: матрица расстояний между объектами.
Подготовить таблицу оптимального пути. Диапазон B 2: F 6 заполнить начальными значениями – нулями.
С помощью функции СУММ найти суммы по строкам и столбцам по оптимальному плану
Ввести дополнительные переменные – диапазон ячеек С 10: F 10.
Заполнить ограничения по дополнительным переменным согласно формулам приведенным на рис. 3.4 (пример представлен для последний строки и последнего столбца).
В ячейку С 9 ввести выражение оптимального плана.
Запустить средство Поиск решения и ввести необходимые параметры: адрес целевой ячейки, изменяемые ячейки и ограничения (рис. 3.5).

Рис.3.5
Требования к отчету
Отчет должен содержать:
титульный лист;
условие задачи;
решение задачи коммивояжера с помощью метода ветвей и границ;
решение задачи коммивояжера в табличном процессоре MC Excel с помощью инструментального средства Поиск решения.
вывод и анализ полученных результатов.
Варианты индивидуальных заданий.
Каждый студент самостоятельно строит в масштабе 1:1000 участок цеха и располагает в произвольном порядке в нем пять лабораторий для контроля качества продукции. Используя методику решения задачи коммивояжера определить наименьший путь перемещения контролера по лабораториям.
Контрольные вопросы
Какие особенности метода ветвей и границ?
Как формулируется задача коммивояжера?
Понятие редукции строк и столбцов матрицы стоимости?
Что означает понятие запрещенные звенья?
Как можно определить запрещенные звенья?
Вторичный штраф как рассчитывается и что обозначает?
Почему задача коммивояжера не может быть решена как задача линейного программирования?
РАБОТА №4. ТРАНСПОРТНАЯ ЗАДАЧА
Цель работы — приобретение навыков решения транспортной задачи с составлением первоначального плана распределения поставок различными методами.
|
|
|
Программное обеспечение: табличный процессор MSExcel.
Теоретическое введение
Транспортная задача в общем виде формулируется следующим образом.
Пусть имеется mпунктов отправления грузов (или пунктов производства) A 1, A 2, А 3,…, Amи nпунктов назначения (или пунктов потребления) B 1, В 2, В 3,…, Bn.Обозначим запасы груза (или ресурсы производства) в i -м пункте отправления через ai,где i = 1, 2,..., m, а потребность каждого j -го пункта потребления через bj,где j = 1, 2,., n.
Заданы стоимости Cjперевозки единицы груза от каждого i -го пункта до каждого j -го пункта потребления. Требуется определить, какое количество груза Xjнеобходимо перевезти из i -го пункта отправления до каждого j -го пункта потребления, чтобы:
вывезти грузы всех поставщиков;
удовлетворить всех потребителей;
достичь минимального значения общей стоимости перевозок.
Условие задачи можно записать в виде таблицы, называемой матрицейпланирования перевозок (табл. 4.1).
Таблица 4.1
| Поставщики | Потребители | Запасы груза | |||||
| B1 | B2 | … | Bj | … | Bn | ||
| A 1 | c11 x11 | c12 x12 | … | c1j x1j | … | c1n x1n | a1 |
| A 2 | c21 x21 | c22 x22 | … | c2j x2j | … | c2n x2n | a2 |
| … | … | … | … | … | … | … | … |
| A i | ci1 xi1 | ci2 xi2 | … | cij xij | … | cin xin | ai |
| … | … | … | … | … | … | … | … |
| Am | ст1 хт1 | ст2 хт2 | … | cnj хmj | … | стп хтп | ат |
| Потребность в грузе | b1 | b2 | … | bj | … | bm | 
|
Строки таблицы соответствуют поставщикам, а столбцы–потребителям. В последней строке записаны заявки каждого потребителя, а в последнем столбце–запасы каждого поставщика.
В верхних правых углах внутренних клеток таблицы записываются истинные тарифы Сj, а в нижних левых углах–планируемые перевозки xj.
Целью решения задачи является составление плана перевозок грузов, обеспечивающих минимальные транспортные расходы.Модель транспортной задачи, для которой количество груза у всех поставщиков равно потребностям всех потребителей в данном грузе, называется закрытой, а сама транспортная задача сбалансированной. Модели, для которых суммарные запасы не равны суммарным потребностям, называются открытыми, а задачи — несбалансированными. Разрешимыми являются только закрытая модель или сбалансированная транспортная задача. Чтобы решить любую транспортную задачу, надо свести ее к закрытой модели, а затем найти решение сбалансированной задачи. Отметим, что любую открытую модель можно свести к закрытой введением фиктивного потребителя либо фиктивного поставщика.
|
|
|
Математическая модель транспортной задачи имеет следующий вид.
Найти минимальное значение функции цели
 (4.1)
(4.1)
при ограничениях

 (4.3)
(4.3)
xij ≥ 0, где i = 1,2,…,m; j = 1,2,…,n. (4.4)
В рассматриваемой модели предполагается, что суммарные запасы равнысуммарным потребностям, т.е
 (4.5)
(4.5)
О п р е д е л е н и е 4.1. Всякое неотрицательное решение систем линейных уравнений (4.2) и (4.3), определяемой матрицей  , где i = 1, 2,..., m;j =1,2,..., n, называется планом транспортной задачи.
, где i = 1, 2,..., m;j =1,2,..., n, называется планом транспортной задачи.
О п р е д е л е н и е 4.2. План  где i = 1,2,..., m; j = 1,2,..., n, прикотором функция (4.1) принимает минимальное значение, называется оптимальным планом.
где i = 1,2,..., m; j = 1,2,..., n, прикотором функция (4.1) принимает минимальное значение, называется оптимальным планом.
Любое решение транспортной задачи называется распределением поставок.При распределительном методе решения транспортной задачи последовательно используются расчетные таблицы, соответствующие тому или иному шагу решения. Каждая такая таблица включает определенное распределение поставок. Так как распределение поставок должно соответствовать базисному решению, то и клетки таблицы должны соответствовать основным (положительным) и неосновным (равным нулю) переменным. На практике в клетки, соответствующие основным переменным, записываются поставки, а клетки, которые соответствуют неосновным переменным, оставляют незаполненными (свободными). Решение транспортной задачи состоит в переходе от одного распределения поставок к другому: от одной таблицы к другой. Новое распределение поставок не должно увеличивать общую стоимость затрат на перевозки. Перераспределение поставок должно осуществляться до тех пор, пока не будет найдено их оптимальное распределение. Чтобы осуществлять переход от одного распределения поставок к другому, надо иметь исходное (первоначальное) распределение поставок.
Решение транспортной задачи обычно проводится в два этапа. На первом этапе находят какое-нибудь решение, удовлетворяющее системе линейных ограничений, или убеждаются, что такое решение не существует. Этот этап называется отысканием исходного опорного плана. На втором этапе проводится последовательное улучшение этого плана по определенным правилам до тех пор, пока не будет найдено оптимальное решение и дальнейшее улучшение станет возможным.
|
|
|
От того, каким будет исходный план, зависит время решения задачи на втором этапе.
Метод наименьшей стоимости
Метод наименьшей стоимости учитывает при построении исходного плана стоимость перевозок, т.е. истинные тарифы сij.
Определение значений xijначинается с клетки, имеющей минимальную стоимость перевозки. Если таких клеток несколько, то выбирают любую из них. В выбранную клетку помещается поставка
 .
.
Строка или столбец, соответствующие наименьшему числу, исключаются из дальнейшего рассмотрения (вычеркивается), а заявка потребителя или наличие запаса у поставщика уменьшается на соответствующую величину.
Если для выбранной клетки ai = bj,то из дальнейшего рассмотрения исключается i-я строка и j -й столбец.
Из оставшейся таблицы вновь выбирают клетку с наименьшей стоимостью и повторяют аналогичные действия до тех пор, пока все запасы не будут распределены, а потребности полностью удовлетворены.
Этот план позволяет получить опорный план транспортной задачи ближе к оптимальному по сравнению с методом северо-западного угла.
Полученный план необходимо проверить на вырожденность. Если количество заполненных клеток равно m + n- 1, то план является невырожденным, если же меньше, то он вырожденный. Если план вырожденный, то среди незаполненных клеток ищут те, у которых минимальные тарифы перевозок. Их заполняют нулевыми поставками так, чтобы общее количество заполненных клеток стало m+ n- 1.
При этом необходимо помнить, что в таблице не должно быть ни одного цикла, все вершины которого являются заполненными клетками.
Циклом в транспортной задаче называется замкнутый многоугольник, одна вершина которой совпадает с той клеткой, для которой он строится, а все остальные вершины совпадают с заполненными клетками. Вершины соединяются замкнутой ломанной линией, отрезки которой в каждой заполнен ной клетке образуют угол 90°.
|
|
|


