Метод северо-западного угла.

Метод состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная с левого столбца и верхней строки, и выписывании максимально возможных отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены заявленные в задаче возможности поставщика или потребности потребителя. На цены доставки в этом методе не обращают внимание, поскольку предполагается дальнейшая оптимизация отгрузок.

Нахождение оптимального плана транспортной задачи

Построенный одним из методов исходный опорный план можно довести до оптимального путем последовательного улучшения.

Существуют несколько таких методов: распределительный, метод потенциалов, венгерский метод и др. Рассмотрим метод потенциалов.

Метод потенциалов

Основой вычислительного процесса при улучшении опорного плана является определение критерия оптимальности:

,

где - расчетные затраты или косвенные тарифы, связанные с доставкойодной единицы груза из i -го пункта отправления в j -й пункт назначения, определяемые для тех клеток опорного плана, ресурсы в которые не распределены (для незаполненных клеток); c_ij— затраты (истинные тарифы), связанные с доставкой одной единицей груза из i -го пункта отправления в j -й пункт назначения.

Т е о р е м а 4.1. Если для всех свободных клеток таблицы перевозок значение критерия оптимальности ≤0, то этот план перевозок является оптимальным.

Если для всех свободных клеток таблицы перевозок значение критерия оптимальности <0, то этот оптимальный план перевозок является единственным.

Если для некоторых свободных клеток значение критерия оптимальности = 0, то этот оптимальный план перевозок не является единственным.

Если имеются свободные клетки, для которых критерий оптимальности >0, то полученный план перевозок не является оптимальным.

Алгоритм метода потенциалов

Каждому поставщику A_i,где i = 1,2,..., т, ставится в соответствие некоторое число U_i,где i = 1, 2,., т, которое называется потенциалом А-гопоставщика или i -й строки.

Каждому потребителю B_j,где j = 1,2,…, п, ставится в соответствие некоторое число V_j,которое называется потенциалом B_j -го потребителя или j-го столбца.

Для каждой заполненной клетки, т.е. для каждой базисной переменной, строитсясоотношение U_i + V_j = c_ij Получают систему с числом уравнений, равным количеству базисных переменных (количеству заполненных клеток).Из этой системы определяют неизвестные потенциалы строк U_iи столбцов V_j.

Поскольку число неизвестных п+ т превышает на единицу число уравнений т+ п-1, одно из неизвестных можно положить равным произвольному числу, например, U₁ = 0 и найти значения остальных неизвестных. Значения потенциалов записываются в ту же матрицу планирования перевозок.

Для каждой незаполненной клетки, т. е. для каждой небазисной переменной, рассчитываются косвенные тарифы по формуле

.

Проверяют полученный план на оптимальность по критерию S _jоптимальности опорного плана транспортной задачи. Если для каждой незаполненной клетки выполняется условие

,то исходный план является оптимальным.

Если некоторое >0, то необходимо перейти к новому базисному планупутем перемещения перевозки в клетку, отвечающую условию max . Еслитаких клеток несколько, то выбирают любую из них.

Для перераспределения поставок строят цикл, соединяющий выбранную клетку с ней же самой и проходящий через заполненные клетки.

Цикл строится следующим образом. Вычеркиваются все строки и столбцы, содержащие ровно одну заполненную клетку. При этом считается, что выбранная клетка без поставки является заполненной. Все оставшиеся после вычеркивания клетки составляют цикл и лежат в его углах. Они соединяются ломаной линией.

Можно доказать, что для любой незаполненной клетки матрицы перевозок существует цикл и он является единственным.

В каждую клетку цикла, начиная с незаполненной, поочередно вписываем знаки «+» и «-». Так как у цикла четное количество вершин, то знаки будут чередоваться по кругу.

В клетках с отрицательными знаками выбирается минимальная величина поставки и обозначается А. В те вершины, которые имеют знак «+» прибавляется еще поставка А, а в вершинах со знаком «-» поставки уменьшают на величину А. При этом суммы поставок по строкам a_iи по столбцам bjне изменятся.

В результате этого действия, называемого пересчетом поставок по циклу, клетка, для которой строился цикл, станет занятой, а в одной из бывших занятых окажется нулевая поставка и ее надо объявить свободной. Общее количество заполненных клеток не изменится, следовательно, новый полученный план перевозок является невырожденным.

Если в результате пересчета одновременно в нескольких ранее занятых клетках поставки примут нулевые значения, то свободной объявляется лишь одна из них. Остальные считаются условно занятыми с нулевыми поставками.

Значения переменных, включенных в цикл, после пересчета переносятся в новую таблицу. Все остальные переменные записываются в новую таблицу без изменений.

Полученный новый базисный план проверяется на оптимальность.

Такое улучшение плана можно проводить до тех пор, пока все критерии для незаполненных клеток окажутся <0. Затем вычисляется оптимальная стоимость перевозок.

Последовательное применение метода потенциалов обеспечивает монотонное убывание значений целевой функции Zтранспортной задачи (общей стоимости перевозок всего груза). Он позволяет за конечное число шагов найти минимум Z.

Алгоритм нахождения оптимального плана перевозок в транспортной задаче.

Оптимальный план перевозок находится по следующей схеме.

Строится исходный опорный план. Если он оказывается вырожденным, то вводятся условно занятые клетки с нулевыми поставками, дополняя число занятых клеток до m + n- 1.

Вычисляется значение целевой функции Z.

Строится система потенциалов, с помощью которой план проверяется на оптимальность. Если условие оптимальности выполнено, решение заканчивается, в противном случае — осуществляется переход к следующему шагу.

Выполняется пересчет поставок по циклу, загружается клетка, для которой не выполняется критерий оптимальности. Строится новый опорный план с числом занятых клеток, равным m + n -1.

Выполняется переход к пункту 3.

Следует иметь в виду, что при решении транспортной задачи возможны случаи вырождения, которые встречаются, если при построении плана перевозок число заполненных клеток окажется меньше, чем m + n- 1. В этом случае следует в свободные клетки ввести недостающее количество поставок, считая их нулевыми, но заполненными. Желательно вводить эти поставки в клетки с наименьшими тарифами. Однако если при выполнении дальнейших расчетов встречаются затруднения, например, происходит зацикливание, надо поменять заполненную нулем клетку.

Порядок выполнения работы

решить транспортную задачу в соответствии с предложенным вариантом с использованием ТП Excel;

найти исходный опорный план методом северо-западного угла для вариантов с нечетным номером и методом наименьшей стоимости для вариантов с четным номером;

найти оптимальный план транспортной задачи методом потенциалов.

Пример выполнения работы

Некоторый однородный продукт, сосредоточенный у трех поставщиков А₁, А₂, A₃ в количестве а₁, а₂, а₃ тонн соответственно, необходимо доставить потребителям B₁, B₂, B₃, B₄, B₅ в количестве b₁, b₂, b₃, b₄, b₅ тонн.

	bi
ai

Стоимость C_ijперевозки тонны груза от i- го поставщика j -му потребителю задана матрицей D. Составить план перевозок, имеющий минимальную стоимость и позволяющий вывести
все грузы и полностью удовлетворить потребности. Исходные данные приведены в табл. 4.2.

На рис. 4.1 приведено решение данной задачи в табличном процессоре MS Excel с помощью инструментального средства Поиск решения. Рис. 4.1

Последовательность решения:

подготовить таблицы и заполнить их исходными данными: Стоимостиперевозки тонны продукта (D), Ресурсы (а) и Потребности (b);

с помощью функции СУММ найти суммы ресурсов (ячейка D 12) и потребностей (G 14);

подготовить таблицу оптимальных перевозок. Диапазон G 09: G 21 заполнить начальными значениями — нулями;

с помощью функции СУММ найти суммы перевозок по потребителям (C 22: G 22) и поставщиками (Н 19: Н 21);

в ячейку G 16 ввести выражение стоимости оптимального плана перевозок;

запустить инструментальное средство Поиск решения (меню Сервис/Поиск Решения) и ввести необходимые параметры: адрес целевой ячейки, изменяемые ячейки и ограничения (рис. 4.2).

Требования к отчету

Отчет должен содержать:

название лабораторной работы;

цель лабораторной работы;

задание;

результат решения в ТП Excel;

исходный опорный план, найденный методом северо-западного угла или методом наименьшей стоимости;

последовательность шагов нахождения оптимального плана методомпотенциала.

 

Рис.4.2

 

 

Варианты индивидуальных заданий

Варианты 1—8.Некоторый однородный продукт, сосредоточенный у трех поставщиков А₁, А₂, А₃ в количестве а ₁, а ₂, а ₃ тонн соответственно, необходимо доставить потребителям В ₁, В ₂, В ₃, В ₄, В ₅ в количестве b ₁, b ₂, b ₃, b ₄, b ₅ тонн. Стоимость C_ijперевозки тонны груза от i- го поставщика j -му потребителю задана матрицей D. Составить план перевозок, имеющий минимальную стоимость и позволяющий вывести все грузы и полностью удовлетворить потребности.

Варианты 9—16.Пусть на предприятии имеется т видов станков, максимальное время работы которых соответственно равно а, где i = 1,2,..., т часов. Каждый из станков может выполнять п видов операций. Суммарное время выполнения каждой операции соответственно b_j, j = 1, 2, п. Известна производительность (C_j)i -го станка при выполнении j -й операции. Определить, сколько времени и на какой операции нужно использовать
каждый из станков, чтобы разработать максимальное количество деталей.

Для решения этой задачи линейную функцию умножить на -1, т.е. считать в таблице все значения C_jотрицательными.

Приведем сходные данные для вариантов

at			bj

at			bj

 

at			bj

at			bj

 

 

at			bj

at			bj

 

 

at			bj

 

at			bj

 

at			bj

at			bj

 

at	bj

at	bj

 

at	bj

at	bj

 

 

at	bj

at			bj

 

at			bj

at	bj

 

Контрольные вопросы

1. Как формулируется транспортная задача?

2. Каков общий вид матрицы планирования перевозок?

3. Что называется планом транспортной задачи?

4. Какие существуют способы отыскания исходного опорного плана?

5. Охарактеризуйте метод северо-западного угла.

6. Охарактеризуйте метод наименьшей стоимости.

7. Какие существуют способы улучшения исходного опорного плана для транспортной задачи?

 

РАБОТА №5. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

 

Цель работы — знакомство с простейшей задачей нелинейного программирования (нахождение оптимального значения функции одной переменной) и одним из методов ее решения — методом золотого сечения. Приобретение навыков решения оптимальных задач встроенными средствами системы MathCAD.

Программное обеспечение: интегрированная математическая система MathCAD.

Теоретическое введение

Разработаны численные методы решения задач минимизации нелинейной функции как при ограничениях, так и без ограничений. Задачи и методы целесообразно изучать по схеме от простого к сложному. Сначала излагаются методы минимизации функции одной переменной. Далее рассматриваются методы для решения задач без ограничений с целевой функцией нескольких переменных. Наиболее сложными являются задачи оптимизации с ограничениями.

Универсального метода, с помощью которого можно было бы успешно решать разнообразные задачи оптимизации с ограничениями, не существует. Поэтому для решения каждого конкретного класса задач используют «свои» численные методы.

Классический метод минимизации функций одной переменной.Рассмотрим задачу нахождения минимума функции f(x) на отрезке [ a; b ]. Классический метод подробно излагается в курсе математического анализа. Основным недостатком классического метода является узкая область его применения.

Если значения целевой функции определены из наблюдений или в результате проведения экспериментов, то получить аналитическое выражение для производной трудно. Но даже если f ' (х) найдена, то отыскание корней уравнения f ' (х)=0 может составить сложную вычислительную задачу. Поэтому разработаны методы минимизации, которые не требуют числового значения производных и в которых объем вычисления значений целевой функции является наименьшим.

Унимодальные функции. Выделим класс функций, обладающих важным свойством.

Функция f(x)называется унимодальнойна отрезке [ a; b ],если онаимеет на этом отрезке единственнуюточку глобального минимума x _min
и слева от этой точки является строгоубывающей, а справа — строго возрастающей.

Другими словами, функция f(x) унимодальная, если точка x _minсуществует и является единственной. Нарис. 5.1 представлен пример графикаунимодальной функции.

Рис. 5.1

Имеет место следующее свойство унимодальной функции. Рассмотрим
две произвольные точки x ₁, x ₂є[ a; b ] и a< x ₁< x ₂<b.

Если f(x ₁) <f (x ₂), то x _min< x ₂(рис. 5.2, а), если же f (x ₁) >f(x ₂), то тогда
x _min> x _i(рис. 8.2, б).

Рис. 5.2

Метод золотого сечения. Будем искать точку глобального минимума унимодальной функции f ( x ) на отрезке [a;b]так, чтобы количество вычислений значений f (x) для заданной точности было наименьшим.

Рассмотрим на исходном отрезке точку x₁и вычислимf ( x ). Зная значение f (x) только в одной точке, невозможно сузить область поиска точки x _min. Поэтому выбираем вторую точку x ₂так, чтобы a< x ₁< x ₂<bи вычисляем f (x ₂).

Возможен один из двух случаев:

f (x ₁) <f(x ₂), согласно свойству унимодальной функции область поиска сужается до [ a; x ₂];

f (x ₁) >f (x ₂), тогда область поиска сужается до [ x ₁; b ].

Где же лучше всего на исходном отрезке брать точки х ₁ и х ₂?

Так как первоначально ничего неизвестно о положении точки x_min, то оба указанных выше случая равно возможны. Отсюда ясно, что точки х ₁ и х ₂ должны быть расположены симметрично относительно середины отрезка [ a; b ].

Чтобы найти «золотую середину», рассмотрим для простотыотрезок [1; 2] (рис. 5.3).

Рис. 5.3

Чтобы точкаВ была «выгодной» как на первом этапе, так и на следующем, она должна делить отрезок ADв таком же отношении, как и АС, т.е.АВ/AD = BC/AC. При этом в силу симметрии аналогичным свойствам будетобладать и точка С.

В терминах координаты х пропорция примет вид

Это уравнение имеет корень меньше 1 и равный .

О точке, которая расположена на расстоянии % длины от одногоиз концов отрезка, говорят, что она выполняет «золотое сечение» данного отрезка. Очевидно, каждый отрезок имеет две такие точки, расположенные симметрично относительно середины.

Итак, точки x ₁и х ₂ должны осуществлять «золотое сечение» исходного отрезка [ a; b ].

Вычисляем координаты точек, осуществляющих «золотое сечение» исходного отрезка, , z₀ =a₀+b₀ - y₀и определяем значения f (y ₀) и f (z ₀).

Сравниваем значения f(y_k - ₁) и f(z_k-₁), (к>1).

Если f(y_k-1) <f(z_k-1), то полагаем a_k = a_k-1, b_k= z_k-1, z_k= y_{k - 1} и вычисляем координату точки (слева от имеющейся) y_k = a_k + b_k-z_kи значение f (y _k).

Если f(y_k-₁) >f(z_k-₁), то полагаем a_k=a_k-₁, b_k=z_k-₁, z_k=y_k-₁ и вычисляем координату точки (справа от имеющейся) z_k = a_k + b_k - y_kи значение f(z_k).

В любом из двух случаев вычисляется длина (k +1)-го отрезка: ∆_k - ₁=b_k-y_kили∆_{k- 1}= z_k-a_k

Работа выполняется до тех пор, пока ∆_k-₁<s, где s>0 — заданная точность вычислений.

Выбираем наименьшее из чисел f(y_k) и f(z_k)— приближенный минимум. А точка, которая ему соответствует, дает приближение к x _min.

Порядок выполнения работы

Решить задачу оптимизации в системе MathCAD по алгоритму:

задать начальные условия задачи оптимизации;

построить график функции f (x);

оформить вычислительный блок Given с привлечением функции maximize или minimize;

получить значения f (х)_опт и х _опт.

Проанализировать полученный результат.

Обратите внимание! Для поиска значений переменных x₁,x₂,…,x_n,при которых функция f (x ₁, x ₂,..., x _n) имеет максимальное или минимальное значение используются функцииmaximize f (x ₁, x ₂,..., x _n) и minimize f(x ₁, x ₂,., x _n). Обе эти функции реализованы достаточно универсальным алгоритмами оптимизации. Эти функции должны использоватьсяв составе вычислительного блока, открываемого директивой Given, и возвращают векторнеизвестных, при котором заданная функция имеет максимальное или минимальное значение. Внутри блока могут быть различные ограничительные условия в виде равенств илинеравенств. Число условий ограничено только памятью ПК. Перед блоком решения нужнозадать начальные значения искомых переменных.

Объективности ради надо заметить, что результаты решения сильно зависят от выбораначальных значений и далеко не всегда имеют погрешность, устраивающую пользователя.

Пример выполнения лабораторной работы

Из круглой заготовки изготавливается пожарное ведро по простой технологии: вырезается сектор, затем полученная таким образом выкройка сворачивается в конус, а шов сваривается.

Длина дуги выкройки становится длиной окружности в основании конуса ,

где R– радиус заготовки; – значение угла вырезки; r – радиус основания конуса.

Высота конуса h, радиус его основания rи радиус заготовки Rсвязаны теоремой Пифагора.

Пусть радиус заготовки равен одному метру: R = 1. Длина окружностиоснования конуса , высота конуса , объемконуса .

Математическая формулировка задачи имеет следующий вид (рис. 5.4).Требуется рассчитать значение угла вырезки а, при котором объем V () будет максимальным, угол задаетсяв радианной мере.

При решении задачи воспользуемся встроенной функциейинтегрированной математической системы MathCADmaximize (f, var l, var2,...), возвращающей значения переменных varl, varl,..., которыедоставляют функции f максимальное значение.

 

 

Рис. 5.4

 

Решение задачи с использованием панели программирования приведено на рис.5.5.

 

Требования к отчету

Отчет должен содержать:

копию документа, созданного в MathCAD;

поясняющие записи из теории по теме лабораторной работы.

 

Варианты индивидуальных заданий

Вариант 1. Вычислить максимальное значение функции f (x) = 72 x + 6 х ²- 8 x ³ - x ⁴наотрезке [1,5; 2]. Точку х* определить с точностью до 0,05.

Вариант 2. Вычислить максимальное значение функции f (x) = 2 х - x 2- e^X на отрезке[1; 1,5]. Точку х* определить с точностью до 0,05.

Вариант 3. Вычислить максимальное значение функции f (х) = 2 sinx – tgx на отрезке[0; π/4]. Точку х* определить с точностью до 0,05.

Вариант 4. Вычислить минимальное значение функции f (х) = 1 - 32 х + 4 х² + х⁴ наотрезке [1; 2]. Точку х* определить с точностью до 0,01.

Вариант 5. Вычислить минимальное значение функции f (х) = 1 + 4 х + 2 х ²+ х ⁴на отрезке [-1; 0]. Точку х* определить с точностью до 0,01.

Вариант 6. Вычислить максимальное значение функции f (х) = 2 + 5 х -

-10 х ²+ 5 х ³- x ⁵на отрезке [-3; -2]. Точку х* определить с точностью до 0,01.

Вариант 7. Вычислить максимальное значение функции f (х) = 3 + 120 х - 4 х ²- х ⁴наотрезке [2,5; 3]. Точку х* определить с точностью до 0,01.

Вариант 8. Вычислить максимальное значение функции f (х) = х - 1 х ²+ 2 х ³- 1 х ⁷наотрезке [1,2; 2]. Точку х* определить с точностью до 0,01.

Вариант 9. Вычислить максимальное значение функции f (х) = 5 х + х ²- 1 х ⁴на отрезке [1; 3]. Точку х* определить с точностью до 0,01.

Вариант 10. Вычислить максимальное значение функции f (х) = 1 + х - 2 х ²+ 4 х ⁴наотрезке [0; 1]. Точку х* определить с точностью до 0,01.

Вариант 11. Вычислить минимальное значение функции f (х) = 2 х + х -
-5 x ³+ 2 x ⁴на отрезке [-1; 0,5]. Точку х* определить с точностью до 0,01.

Вариант 12. Вычислить минимальное значение функции f (х) = 2 х + (х + 1)4на отрезке [-3; -1]. Точку х* определить с точностью до 0,01.

Вариант 13. Вычислить минимальное значение функции f (х) = 2 х + х - 5 х на отрезке [-1; -0,5]. Точку х* определить с точностью до 0,01.

Вариант 14. Вычислить максимальное значение функции f (х) = х - 2х + 5 х на отрезке [1; 2]. Точку х* определить с точностью до 0,01.

Вариант 15. Вычислить максимальное значение функции f (х) = 1 - 6 х - 3 х ²- х ⁶наотрезке [-1; 0]. Точку х* определить с точностью до 0,01.

Вариант 16. Вычислить максимальное значение функции f (х) = 80 х - 30 х ²- наотрезке [1; 2]. Точку х* определить с точностью до 0,01.

Вариант 17. Вычислить максимальное значение функции f (х) = 1 + 2 х + - наотрезке [1; 1,5]. Точку х* определить с точностью до 0,01.

Вариант 18. Вычислить минимальное значение функции f (x) = 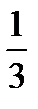x ² + x (ln x -1) наотрезке [0,5; 1]. Точку х* определить с точностью до 0,01.

Вариант 19. Вычислить максимальное значение функции f (x) = x ³ - e^x - 2 x на отрезке [-2; 1]. Точку х* определить с точностью до 0,01.

 

Контрольные вопросы

1. В чем состоит классический метод оптимизации функции одной переменной?

2. Какие функции называются унимодальными?

3. В чем состоит суть метода золотого сечения?

4. Какая точка выполняет золотое сечение отрезка [0;1]?

 

 

 

Рис. 5.5

 

 

 

РАБОТА №6. ПЛАНИРОВАНИЕ РАБОЧЕЙ СИЛЫ

 

Число рабочих, необходимых для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Поскольку как наем, так и увольнение рабочих связано с дополнительными затратами, необходимо определить, как должна регулироваться численность рабочих в период реализации проекта.

Предположим, что проект будет выполняться в течение n недель и минимальная потребность в рабочей силе на протяжении i -й недели составит b _i рабочих. При идеальных условиях хотелось бы на протяжении i -й недели иметь в точности b _i рабочих. Однако в зависимости от стоимостных показателей может быть более выгодным отклонение численности рабочей силы как в одну, так и в другую сторону от минимальных потребностей. Если x _i – количество работающих на протяжении i -й недели, то возможны затраты двух видов:

C ₁(x _i – b _i) – затраты, связанные с необходимостью содержать избыток x _i – b _i рабочей силы

C ₂(x _i – x _i-1) – затраты, связанные с необходимостью дополнительного найма x _i – x _i-1 рабочих.

Элементы модели динамического программирования определяются следующим образом.

Этап i представляется порядковым номером недели i, i = 1,2,..., n.

Вариантами решения на i -м этапе являются значения x _i – количество работающих на протяжении i -й недели.

Состоянием на i -м этапе является x _i-1 – количество работающих на протяжении (i – 1)-й недели (этапа).

Рекуррентное уравнение динамического программирования представляется в виде

, i = 1, 2, …, n,

где f_n +1(x _n) º 0

Вычисления начинаются с этапа n при х _n = b _n и заканчиваются на этапе 1.

Пример 1. Для реализации проекта строительный подрядчик определил минимальные потребности в рабочей силе на ближайшие пять недель следующим образом: 5, 7, 8, 4 и 6 рабочих соответственно. Содержание избытка рабочей силы обходится подрядчику в 300 долларов за одного рабочего в неделю, а наем рабочей силы на протяжении одной недели обходится в 400 долларов (независимо от количества принимаемых на работу человек) плюс 200 долларов за обучение одного нового рабочего в неделю.Необходимо определить, каким образом должна регулироваться численность рабочих в период реализации проекта. Задачу решить методом динамического программирования.

Решение. Выражая затраты в сотнях долларов, имеем:

b ₁=5, b ₂=7, b ₃=8, b ₄=4, b ₅=6,

C ₁(x _i- b _i)=3(x _i- b _i), x _i> b _i, i =1, 2, 3, 4, 5,

C ₂(x _i- x _i-1)=4+2(x _i- x _i-1), x _i> x _i-1,, i =1, 2, 3, 4, 5.

Решение задачи начинаем с последнего (5-го этапа). По условию на этом этапе должно работать 6 работников. На предыдущем этапе в штате могло быть 4 (необходимый минимум), 5 или 6 работников (с учетом численности на 5-ом этапе).

Этап 5. (b ₅=6)

Табл.6.1

x 4	С 1(х 5-6)+ С 2(х 5- х 4)	Опт.решение
х 5 = 6	f 5(x 4)	x 5*
	3(0)+4+2(2)=8
	3(0)+4+2(1)=6
	3(0)+0=0

 

На четвертом этапе должно работать 4 работника, однако, учитывая, что на следующем этапе потребуется 6 исполнителей, в штате может быть 4, 5 или 6 человек. Поэтому в таблице 6.1 х ₄ = 4, 5, 6.

Этап 4. (b ₄=4) Табл.6.2

x 3	С 1(х 4-4)+ С 2(х 4- х 3)+ f 5(x 4)	Опт.решение
х 4 = 4	х 4 = 5	х 4 = 6	f 4(x 3)	x 4*
	3(0)+0+8=8	3(1)+0+6=9	3(2)+0+0=6

 

На третьем этапе должно работать максимальное число (8) работников. Поэтому в таблице 6.2 х ₃ = 8.

 

Этап 3. (b ₃=8)

Табл.6.3

x 2	С 1(х 3-8)+ С 2(х 3- х 2)+ f 4(x 3)	Опт.решение
х 3 = 8	f 3(x 2)	x 3*
	3(0)+4+2(1)+6=12
	3(0)+0+6=6

 

На втором этапе в штате может быть 7 исполнителей (необходимый минимум) или 8 исполнителей (с учетом потребностей следующего этапа). Поэтому в таблице 6.3 х ₂ =

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: