 |
В) дифференциальный манометр
|
|
|
|
Рисунок 14 – Жидкостные приборы для измерения давления
Для уменьшения длины измерительной трубки применяют приборы с жидкостью большей плотностью (например, ртутью). Ртутный манометр представляет собой У-образную трубку, изогнутое колено которого заполняется ртутью (рис. 14б). Под действием давления в сосуде уровень ртути в левом колене манометра понижается, а в правом - повышается.
Дифференциальный манометр применяют в тех случаях, когда необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или в двух точках одного сосуда (рис. 14 в).
Применение жидкостных приборов ограничивается областью сравнительно небольших давлений. Если необходимо измерять высокие давления, применяют приборы второго типа -механические.
Пружинный манометр является наиболее распространенным из механических приборов. Он состоит (рис.15а) из полой тонкостенной изогнутой латунной или стальной трубки (пружины) 1, один конец которой запаян и соединен приводным устройством 2 с зубчатым механизмом 3. На оси зубчатого механизма располагается стрелка 4. Второй конец трубки открыт и соединен с сосудом, в котором замеряется давление. Под действием давления пружина деформируется (распрямляется) и через приводное устройство приводит в действие стрелку, по отклонению которой определяют значение давления по шкале 5.
| P |
| Р |
а) пружинный манометр б) мембранный манометр
Рисунок 15 - Механические приборы для измерения давления.
Мембранные манометры также относятся к механическим (рис. 15б). В них вместо пружины устанавливается тонкая пластина-мембрана 1 (металлическая или из прорезиненной материи). Деформация мембраны посредством приводного устройства передается стрелке, указывающей значение давления.
|
|
|
Механические манометры имеют по сравнению с жидкостными некоторые преимущества: портативность, универсальность, простоту устройства и эксплуатации, большой диапазон измеряемых давлений.
Для измерения давлений меньше атмосферного применяют жидкостные и механические вакуумметры, принцип работы которых тот же, что и у манометров.
9. Определение сил гидростатического давления покоящейся жидкости на плоские стенки.
Определим как рассчитывается сила гидростатического давления на плоскую стенку, которая наклонена под углом 
, при одностороннем воздействии жидкости (рис. 18). Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью 
. Между любой координатой у и глубиной погружения h существует следующая связь: 
.
|
|
|
|
|
|
|
|
|
|
|
| C |
| C |
| D |
| D |
d 
|
Рисунок 18 - К определению силы давления на плоскую стенку.
На каждый бесконечно малый элемент площади 
действует элементарная сила 
, но давление в центре тяжести 
равно 
.
Тогда элементарная сила 
.
Суммарная сила давления на всю площадь со может быть получена интегрированием по площади 
:
,
где 
- статический момент площади относительно оси ОХ.
Известно, что статический момент площади равен произведению координаты центра тяжести на площадь фигуры:
,
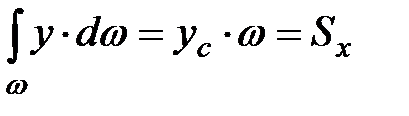откуда можно записать, что суммарная сила гидростатического давления равна:
или 
,
где 
- давление в центре тяжести.
Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести этой поверхности на ее площадь.
|
|
|
Центром давления называется точка приложения полной силы гидростатического давления, действующей на данную поверхность.
Для определения положения центра давления воспользуемся известной теоремой статики: момент равнодействующей силы равен сумме моментов сил ее составляющих.
Т.е. 
.
Из этого выражения можно найти искомую координату центра давления (точки D):
,
где 
- момент инерции площади относительно оси ОХ.
Но момент инерции относительно любой оси может быть выражен через моментинерции относительно центральной оси 
(оси, проходящей через центр тяжести фигуры).
,
где а - расстояние между осями (в нашем случае 
)
Тогда 
или 
.
Используя уравнение связи между глубиной h и координатой y, получим уравнение для определения глубины погружения центра давления:
.
Это выражение показывает, что центр давления лежит всегда ниже центра тяжести (кроме давления на горизонтальную плоскость, когда они совпадают).
|
|
|
