Предисловие. 1. Представление чисел в различные системы счисления

Методические указания к выполнению контрольных заданий по информатике

Предисловие

 

Программа курса " Информатика " составлена в объеме, необходимом для изучения общенаучных, общеинженерных и экономических дисциплин и развития навыков, требуемых для применения вычислительной техники в практике работы инженера, экономиста и научного работника.

Настоящее издание предназначено для студентов-заочников технических специальностей и содержит задания для контрольных работ.

В результате изучения курса студенты должны:

§ знать формы представления числовой информации в различных системах счисления и уметь переводить числа из одной системы счисления в другую;

§ знать основы алгебры логики и уметь формировать и упрощать логичес­кие формулы и переключательные схемы.

1. Представление чисел в различные системы счисления

 

Система счисления – это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображеия числ системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционной системе счисления цифры не имеют своего количественного значения при изменении их расположения в числе. Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до Р-1. В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида

 

 a_m-1P^m-1+a_m-2P^m-2+…+a₁P¹+ a₀P⁰+a_-1P^-1+a_-2P^-2+…+a_-sP^-s,      (1) 

 

где нижние индексы определяют местоположение цифры в числе (разряд):

· Положительные значения индексов – для целой части числа (m разрядов);

· Отрицательные значения – для дробной (s разрядов).

Для перевода целого десятичного числа N в систему счисления с осно­ванием q необходимо разделить N на q с остатком. Затем неполное частное, полученное от этого деления, нужно снова разделить на q с остатком и т. д., пока последнее полученное неполное частное не станет равным нулю. Число N в системе счисления с основанием q представится в виде упорядоченной по­следовательности полученных остатков деления, записанных одной q-ичной цифрой в порядке, обратном порядку их получения(табл. 1. ).

Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q и т. д. до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, за­писанных в порядке их получения и изображенных одной q -ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется .

Пример.     Переведем число 0, 36 из десятичной системы (рис. 1. ) в:  

а) двоичную;

б) восьмеричную;

в) шестнадцатеричную.

 

а) 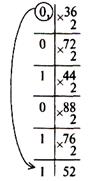           б)                в)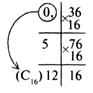

Рис. 1. Пример перевода чисел в различные системы счисления

 

Ответ: а) 0, 36₁₀= 0, 01011₂ с предельной абсолютной погрешностью (2^-6)/2= 2^-7.

   б) 0, 36₁₀= 0, 270₈ с предельной абсолютной погрешностью (8^-4)/2 = 2^-13.

в) 0, 36₁₀= 0, 5С₁₆ с предельной абсолютной погрешностью (16^-3)/2 = 2^-13.

 Для чисел, имеющих как целую, так и дробную часть, пере­вод из десятичной системы счисления в другую осуществляется от­дельно для целой и дробной частей по уже указанным правилам.

Таблица 1

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: