Сводная таблица переводов целых чисел

Сводная таблица переводов целых чисел

Номер перевода	Перевод	Номер перевода	Перевод
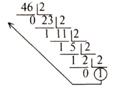
	10-> 2 Ответ: 1011102		2-> 10      1011102=25+23+22+21=4610 Ответ: 4610
			2-> 16   1011102=10 11102=2E16 Ответ: 2Е16
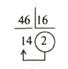
	10-> 8 Ответ: 568		8-> 2 568 =1011102 Ответ: 1011102
			8-> 10      568=5*81+6*80=40+6=4610 Ответ: 4610
	10-> 16 Ответ: 2Е16		8-> 16   568=1011102=10 11102=2Е16 Ответ: 2Е16
			16-> 2 2Е16=001011102= 1011102 Ответ: 1011102
	2-> 8 1011102=1011102=568 5 6 Ответ: 568		16-> 8 2Е16=10 11102= 1011102=568 Ответ: 568
			16-> 10   2Е16=2*161+Е*160 = = 32 + 14 = 4610

1. 1  Перевод чисел из двоичной, восьмеричной               и шестнадцатеричной системы счисления в десятичную

 

Перевод в десятичную систему числа х, записанного в q-й системе счисления (q = 2, 8 или 16) в виде

x_q = (а_па_п-1... а₀, а_-1 a_-2... а_-m)_q,

сводится к вычислению значения многочлена

х₁₀ = a_n qⁿ + a_n-1 q^n-1+... + a₀q⁰ +а_-1 q^-1 + а_-2 q^-2 +... + a_-m q^-m

средствами десятичной арифметики.

Примеры:   1) Разряды 3 2 1 0 -1

Число  1 0 1 1, 1₂ = 1*2³+ 1*2¹ + 1*2⁰ + 1*2^-1 = 11, 5₁₀.

   2) Разряды 2 1 0 -1

  Число  2 7 6, 5₈ = 2*8² + 7*8¹ + 6*8⁰ + 5*8^-1 = 190, 625₁₀.

   3) Разряды 2 1 0

Число  1 F 3₁₆ = 1*16² + 15*16¹ + 3*16⁰ = 499₁₀.

2. Основные законы алгебры логики

 

Алгебра логики – это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1 и оперирующие с логическими высказываниями.

Модели алгебры и исчисления высказываний рассматривают связи между высказываниями, которые воспринимаются через выражающие их предложения.

Операциями в алгебре логики являются операции ло­гического сложения (иначе, операция ИЛИ, операция дизъюнкции) и логического умножения (иначе, операция И, операция конъюнкции). Для обозначения операции логического сложения используют символы + или 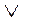, логического умножения - символы * или  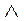, а также импликации  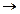и эквивалентности ~ или .

Отрицанием (или инверсией) высказывания х называется новое высказывание, обозначаемое 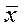(  х), которое читается «не х» и считается истинным, если х ложно, и ложным, если х истинно.

Дизъюнкцией или логической суммой двух высказываний х и у называется новое высказывание, обозначаемое символом х+у (читается: х или у), которое считается истинным, если хотя бы одно из высказываний х или у истинно, и ложным, если оба они ложны.

Конъюнкцией или логическим умножением  двух высказываний х и у считается новое высказывание, обозначаемое ху (х 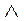у, читается: х и у), которое истинно, если оба высказывания х и у истинны, и ложно, если хотя бы одно из них ложно.

Импликацией двух высказываний х и у называется новое высказывание, обозначаемое символом х 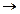у (читается: «если х, то у»), которое считается ложным, если х истинно и у ложно, и истинным при всех других логических значениях высказываний х и у. Высказывание х называется условием или посылкой, высказывание у - заключением или следствием импликации.

Под эквивалентностью высказываний х и у понимается новое высказывание, обозначаемое символом х у (читается: «х тогда и только тогда, когда у» или короче: «х эквивалентно у»), которое считается истинным, когда оба высказывания х и у либо истинны, либо ложны, и ложным в остальных случаях.

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений (табл. 2. )

Таблица 2

Основные законы алгебры логики

Закон	Для ИЛИ	Для И
Переместительный
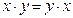
Сочетательный
Распределительный
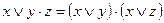
Правила де Моргана
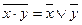
Идемпотенции
Поглощения
Склеивания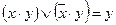
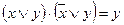
Операция переменной с ее инверсией
Операция с константами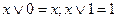
Двойного отрицания

2. 1. Основные соответствия элементов и операций булевых алгебр

 

Множества	Логические функции	Случайные события
		невозможное
U(универсальное)		достоверное
È (объединение)	v (дизъюнкция)	сумма
Ç (пересечение)	& (конъюнкция)	произведение
¾ (дополнение)	(отрицание)	противоположное

                                              

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: