Булевы функции 2-х переменных. 3. Составление таблиц истинности для логических формул. 3.1. Составление логических выражений

Булевы функции 2-х переменных

Табл. 3 содержит все булевы функции двух переменных. Функция g_i имеет в качестве столбца значений двоичную запись числа i. Ниже приведены выражения этих функций формулами.

Таблица 3

X

Y

g0

g1

g2

g3

g4

g5

g6

g7

g8

g9

g10

g11

g12

g13

g14

g15

I

1,

 

g₀ = 0                                                - константа О

g₁ = X & У                                      - конъюнкция

g₂ = (X 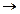 У) = X & У                    - отрицание импликации

g₂= X                                                - первая переменная

g₄ = (у 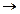X) = X & У                   - отрицание обратной импликации

g₅ = Y                                               -вторая переменная

g₆ = X©Y = X& YvX& Y       - сумма по модулю 2

g₇= Xv У                                         - дизъюнкция

g ₈ = (X & У) = Х v Y          - отрицание конъюнкции

g ₉ = X ~ У = X & Y v X & У        - эквивалентность

g₁₀ ⁼ Y                                           - отрицание второй переменной

g₁₁ = У 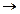 X = X v У                    - обратная импликация

g₁₂ = X                                           - отрицание первой переменной

g₁₃ = X 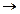 У = X v У                    - импликация

g₁₄ = X | У =Х v У =(Х& У)      - штрих Шеффера

g₁₅ = 1                                               - константа 1

 

3. Составление таблиц истинности для логических формул

 

Согласно определению, таблица истинности логической фор­мулы выражает соответствие между всевозможными наборами значе­ний переменных и значениями формулы. Для формулы, которая содержит две переменные, таких на­боров значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1). Если формула содержит три переменные, то возможных на­боров значений переменных восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Количество наборов для формулы с четырьмя переменными равно шестнадцати и т. д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая, кроме значений переменных и значе­ний формулы и значения промежуточных формул.

Пример. Составим таблицу истинности для формулы , которая содержит две переменные: х и у. В первых двух столбцах таблицы запишем че­тыре возможные пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим табл. 4.

 

Таблица 4

Переменные		Промежуточные логические формулы					Формула
X	У	X

 

Из табл. 4 видно, что при всех наборах значений переменных х и у формула  принимает значение 1, т. е. является тождественно-истинной.

3. 1. Составление логических выражений

Пример. Составьте логическое выражение (формулу), истинность которого обозначает попадание (принадлежность) точки с координатами (х, у) в выделенную на рисунке область, включая ее граничные линии (рис. 2).

Рис. 2. Пример представления логического выражения

 

Выделенная область представляет собой части кругов радиусов R и r. Обозначим эти круги именами К1, К2, КЗ и К4 так, как указано на рисунке справа. Обозначим также отдельные части выделенной области римскими цифрами. Точка принадлежит заданной области, если она находится в одном из фрагментов I.. VI. Отсюда следует, что условие попадания точки в любую часть заданной области есть дизъюнкция условий попадания в отдельные фрагменты. Поскольку фрагменты являются пересечениями отдельных кругов, условия принадлежности точки к фрагменту есть конъюнкция условий соответствующих кругов.

Последовательность решения задачи следующая:

· выразим условия для фрагментов через условия попадания в исходные круги. Условие попадания в круг Ki обозначим тем же именем, т. е. если точка попала в круг Ki, логическая переменная Ki имеет значение истина, иначе - ложь;

· сформируем суммарную логическую формулу, выражающую условие    попадания   в   любую  часть  заданной  области.  Если возможно, попытаемся упростить полученную формулу;

· выразим условия Ki через заданные радиусы r и R и подставим в

формулу, полученную на предыдущем шаге. Некоторое упрощение формулы может быть сделано после этого.

Фрагмент I:         K1× (х < 0)× ;

Фрагмент И:       К4× (х < 0)× ;

Фрагмент III:      К3× × ;

Фрагмент IV:       К4× (х < 0)× ;

Фрагмент V:        К2× (х < 0)× ;

Фрагмент VI:       К3× (х > 0).

 

Вся заданная область:

K1× (х < 0)× +К4× (х < 0)× +К3× × +К4× (х < < 0)× +К2 × (х < 0)× +К3× (х > 0).

Выразим Ki через R и r:

К1 = (х + r)² + у² ≤ R²;  = (х + r)² + у² > R²;

К2 = (х - r)² + у² ≤ R²;  = (х – r)² + у² > R²;

К3 = х² + (у + r)² < R²;  = х² + (у + r)² > R²;

К4 = х²+у²≤ r².

На этом решение задачи можно считать законченным, так как подстановка 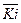 и Ki в результирующую формулу тривиальна и сводится к правильному переписыванию алгебраических выражений, а очевидных путей упрощения формулы в данном случае не просматривается.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: