 |
4. Методы измерений (метод непосредственной оценки, метод сравнения с мерой, метод противопоставления, дифференциальный метод, нулевой метод, метод совпадения, метод замещения).
|
|
|
|
4. Методы измерений (метод непосредственной оценки, метод сравнения с мерой, метод противопоставления, дифференциальный метод, нулевой метод, метод совпадения, метод замещения).
М-ды измерений
Отсчет количества измеряемой величины наиболее точно производится по шкале отношений посредством сравнения его с уже известным размером и выражение его в кратных или дольных единицах.
В квалиметрии известным является представление об эталонном, базовом или наивысшем качестве.
Поэтому ур-е измерений записывается в квалиметрии: 
(1), где Q и QБАЗ выражаются в баллах, а отсчетом по шкале отношений яляется значение безразмерного показателя качества.
При измерении физических величин, их размер сравнивается с размером соответствующей единицы международной системы, а ур-е измерений: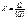 
(2).
Уравнение измерений выражает некоторое действие – процедуру сравнения, которое собственно и является измерением. При органолептическом способе измерений сравнение происходит в уме.
При измерении помощью технических средств неизвестный размер сравнивается с размером единицы, информация о которой хранится средством измерения. Результатом сравнения Х в уравнениях (1) и (2) является величина, зависящая от многих причин и всегда является случайной.
Для сравнения известного размера с неизвестным существуют следующие м-ды:
1) м-д непосредственной оценки, в котором для выражения неизвестного размера через известный используется информация об известном размере - QБАЗ и [Q]. Значение определяемой величины определяется при этом в уме или по отсчетному устройству;
2) м-д сравнения с мерой – информация об известном размере представлена в овеществленной форме, т. е. в виде меры, с которой и сравнивается измеряемая величина.
|
|
|
Разновидность м-да сравнения с мерой
М-д противопоставлений. Когда измеряемая величина и величина, воспроизводимая мерой, одновременно воздействует на компаратор. С помощью этого м-да устанавливается соотношение между ними (мерой и измеряемой величиной). Пример – измерение массы на рычажных весах.
Дифференциальный м-д. При его использовании на ср-ва измерения воздействует разность измеряемой вел-ны и вел-ны, воспроизводимой мерой.
Нулевой м-д. В этом случае разность межуд измеряемой величиной и величиной, воспроизводимой мерой доводят до 0, как при балансировке балансировочного моста.
М-д совпадения. В этом случ разность измеряют используя совпадения меток и шкал. Напр. штангенциркуль.
М-д замещения. Когда неизвестная величина заменяется известной, воспроизводимой мерой.
Разновидности м-дов измерений непрерывно совершенствуются, развиваются и уточняются, но из сущность сравнения информации об измеряемом размере с информацией об известном, остается неизменной.
5. Измерительная информация (априорная и апостериорная).
Она делится на: 1) априорную (до измерения) и 2)апостариорную (после измерения).
Априорная информация очень нужна. Если она отсутствует, то измерения провести невозможно, т. к. неизвестно, что измерять, какие для этого требуются м-ды, ср-ва и т. д. С другой стороны, если об измеряемой величине известно все, то измерения не требуются. Априорная инф-ция есть всегда. Анализ ее проводится до измерений, исходя из поставленной задачи. Уточняются физические св-ва явления, размерность измеряемой величины, при необходимости строится математическая модель, определяется область изменения измеряемых величин, требования к точности измерений. На основе априорной инф-ции выбираются м-д и ср-ва измерений. Априорная информация м. б. почерпнута из накопленного опыта, книжных источников, Интернета. Без этого невозможно организовать измерения. По существу любое измерение – лишь уточнение значения измеряемой величины путем сравнения ее размера с известным размером более точно.
|
|
|
Мерой неопределенности истинного значения измеряемой величины является априорная энтропия. С учетом априорной информации о числовом значении измеряемой величины X, энтропия H0(x) (0 указывает на априорную информацию) определяется интервалом шкалы [x1…xn] в пределах которого может оказаться измеренное значение, а также числом делений шкалы n-1 на интервале с вероятностью Р0i того, что результат измерения окажется в пределах i-го деления.
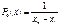
С увеличение числа делений n из уравнения видно, что априорная информации возрастает и, казалось бы, в результате измерения можно получить сколь угодно большое количество информации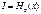 
. Но это не так. Напр., способность человека-эксперта различать градации в проявлении к-л св-в ограничена. Так при стобальной системе человек-эксперт оперирует в лучшем случае величинами, отличающимися друг от друга на 5 баллов. Иначе говоря, точность органолептических м-дов в квалиметрии не превышает 10%.
Применение инструментальных м-дов измерений позволяет увеличить число градаций на интервале неопределенности от х1 до хn и увеличить число информации, получаемой в результате измерения, т. е. повысить точность его результата.
Для количественной оценки обозначим цену деления равномерно шкалы хi+1-х1, соответствующая разрешающей способности средств измерения хi+1-х1=∆ х. А априорную плотность распределения вероятности результата измерения 
.
.
Если бы можно было реализовать бесконечно высокую разрешающую способность и абсолютно точно измерить истинное значение измеряемой величины, то апостарионая информация Н(х) оказалась бы равна 0, а кол-во информации, полученное в результате измерения: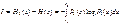 
. На практике это невозможно и после измерения всегда остается некоторая неопределенность, характеризуемая апостариорной энтропией: 
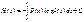. Т. о. в результате любого измерения происходит лишь сужение интервала неопределенности.
Количество получаемой в результате сужения диапазона информации определяется как, 
|
|
|
Трактовка измерения как сужения интервала неопределенности подчеркивает роль априорной информации. Чем ее больше, чем уже исходный интервал неопределенности, тем точнее средствами с высокой разрешающей способностью м. б. измерена величина.
Вывод: накопление априорной информации об измеряемых величинах важное направление повышения точности измерений.
К априорной информации относится и информация о плотности распределения вероятности результата измерения Р0(х) А если ее нет, то естественно принять плотность распределения вероятности истинного значения измеряемой величины на интервале [x1…xn] равномерной. Тогда с точностью до С мы можем записать:
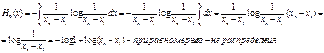
Если з-н распределения нормальный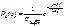 
, то 
|
|
|
