 |
6. Основной постулат метрологии: результат измерения является случайной величиной.
|
|
|
|
6. Основной постулат метрологии: результат измерения является случайной величиной.
Важнейшей апостарионой информацией, ради которой и производится измерение, является результат измерения. Он не тождественен истинному значению измеряемой величины. Аксиома - основной постулат метрологии(опм): результат измерения является случайной величиной.
Отсюда следует, что хотя истинное значение измеряемой величины существует, определить его невозможно. 1-ая часть этого положения является отражением материалистической концепции в естествознании, 2-ая – обнаруживает противоречие, на разрешении которого и основывается прогресс в области измерений.
Из опм следует, что результат измерения субъективен. Специалисты неодинаковой квалификации, используя разные м-ды и ср-ва измерения одной и той же величины, в различной степени приближаются к установлению истинного значения. Для того, чтобы в таких условиях обеспечить единство, сопоставимость, достоверность, точность, правильность и объективность измерений, все виды метрологической деятельности д. б. строго регламентированы. Этим объясняется наличие законодательной метрологии, т. е. системы стандартов в области метрологического обеспечения, большого числа методик, методических указаний (МУ), технических условий (ТУ), технических требований (ТТ), руководящих документов (РД) и другой нормативно-технической документации органов гос. надзора и ведомственного контроля за соблюдением метрологических правил, требований и норм гос-ой и ведомственной метрологических служб. Общий круг этих вопросом объединяется общим понятием и составляет содержание прикладной метрологии.
|
|
|
7. Истинное и действительное значение измеряемой величины.
Т. к. истинное значение измеряемой величины определить невозможно, то с помощью измерений определяют так. наз-ое действительное значение, которое используют на практике вместо истинного (действительное значение м. б. уточнено с помощью устройства с меньшей погрешностью).
З-н распределения вероятности распространения результата измерения Р(х) м. относиться как к априорной так и к апостарионой информации. В 1-ом случае он известен до измерения, во 2-ом – определяется экспериментально по результатам измерения. В обоих случаях этот з-н характеризует неопределенность результата измерения. Она также отражает и нехватку знаний об измеряемой величине при определенных условиях измерения.
8. Неопределенность результата измерения.
Неопределенность результата измерения обусловлена двумя причинами:
1)случайным характером отсчета; 2) дефицитом измерительной информации.
1. Случайный характер отсчета учитывается ее вероятностью. Исчерпывающей характеристикой этой вероятности является з-н распределения вероятности.
Обычно если на отсчет Х влияет мн-во независимых факторов, вклад каждого из которых незначителен по сравнению с общим действием, центральная предельная теорема вероятности гласит, что плотность распределения вероятности подчиняется нормальному з-ну. Если условия этой теоремы не выполняются, то Х подчиняется другим з-нам распределения вероятности.
2. Возникновение неопределенности результата измерения из-за дефицита измерительной информации можно представить следующим примером.
При измерении прибором классом точности 1, 5 истинное значение измеряемой величины отличается от действительного на ±1, 5%. При назначении класса точности прибору учитывается возможный разброс его метрологических характеристик. Однако, реальный прибор имеет реальные метрологические характеристики, обуславливающие отклонение го показаний.
|
|
|
В 1981г. Международный комитет мер и весов рекомендовал дефицит информации, состоящий в неопределенности значений неслучайной величины, учитывать используя распределение вероятности этого значения.
Если нет к-л оснований считать к-л значения более вероятными, то плотность распределения вероятности истинного значения на интервале ±1, 5% можно принять равномерной. Если же, например, известно, что прибор входит в партию приборов, дающих завышенные показания, то это можно учесть выбором соответствующего з-на распределения вероятности на интервале ±1, 5%. Для этого необходимо вычислить энтропию этого распределения и по ф-ле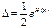 
(#) найти интервал неопределенности. Необходимо подчеркнуть, что здесь речь идет о математической модели неопределенности, что само по себе смещение отсчета, о котором отсутствует необходимая информация, не является случайным.
Чтобы не забывали об этом международный комитет мер и весов величину, аналогичную дисперсии обозначил через U2. Мерой неопределенности результата измерения, обусловленной 2-м рассмотренными выше причинами, м. б. суммарная энтропия и выраженный через (#) интервал неопределенности.
Композиция 2-х з-нов распределения, аналог ее дисперсия, м. записать:
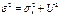или среднеквадратическое отклонение 
.
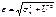А также выбрать аналог доверительного интервала ±кε, где значение коэф. к=1, 2, 3, … устанавливается методами законодательной метрологии.
При неопределенности результата измерения, обусловленной n факторами, имеющими случайную природу и m факторами – неслучайными обстоятельствами, точный учет которых невозможен:
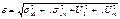
Любые высокоточные измерения должны содержать полный список причин неопределенности с указанием способа учета каждой из этих причин.
9. Законы распределения вероятности:
Закон распределения вероятности результата измерения P(x) может относиться как к априорной, так и к апостариорной информации. В 1-ом случае он известен до измерения, во 2-ом – определяется экспериментально по результатам измерения. В обоих случаях этот закон характеризует неопределенность результата измерения. Он также отражает и нехватку знаний об измеряемой величине при определенных условиях.
|
|
|
1. Равномерный. Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:
,
|
|
|
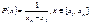