 |
2. Треугольный (Симпсона).. 10. Числовые характеристики законов распределения вероятности (дисперсия, среднее квадратическое отклонение), доверительный интервал, доверительная вероятность.
|
|
|
|
2. Треугольный (Симпсона).
????? 
3. Нормальный (Гаусса). Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:
, Таким образом, нормальное распределение определяется двумя параметрами: 
и σ. График плотности нормального распределения называют нормальной кривой (кривой Гаусса):
4. Нормированный нормальный (стандартное нормальное распределение). Нормальное распределение с параметрами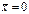 
, σ = 1 называется нормированным:
,
5. Распределение Накагами: 
, где Г(·) – гамма-функция; x≥ 0, параметры распределения: α > 0 и β > 0.
? 
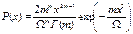, Г(·) – гамма-функция. Используется в системах радиосвязи. Параметры распределения: Ω - средняя мощность замирающего сигнала, m – глубина замираний.
6. Релея.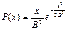 
, В – параметр.
7. Максвелла. χ -распределение с n степенями свободы: 
.
При n=3 это выражение называется плотностью распределения Максвелла и имеет вид: 
.
8. χ -распределение модуля многомерного нормального вектора:
n-мерная непрерывная случайная величина имеет нормальное распределение, если ее многомерная плотность вероятности в матричном виде
9. Пирсона (χ 2-распределение) с n степенями свободы: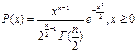 
.
10. Стьюдента.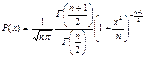 
11. Фишера со степенями свободы m и n:
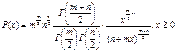
12. Коши с параметрами: 
13. Бета-распределение с параметрами α и β:
, где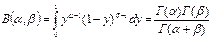 
- бета-функция.
14. Гамма-распределение (Эрланга) с параметрами α, λ > 0:
, где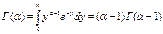 
.
15. Вейбула с параметрами α, λ > 0:
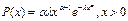
16. Экспоненциальный односторонний (показательный) с параметром λ > 0:
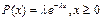
17. Экспоненциальный двусторонний (Лапласа) с параметрами аєR, λ > 0^
18. Арксинуса: 
10. Числовые характеристики законов распределения вероятности (дисперсия, среднее квадратическое отклонение), доверительный интервал, доверительная вероятность.
|
|
|
Использование з-нов распределения вероятности предпочтительно, но не всегда удобно, т. к. это очень трудоемкий процесс. На практике получили широкое распространение цифровые характеристики з-нов распределения (моменты). Они представляют собой некоторые средние значения. Причем, если усреднение идет от начала координат, то моменты называются начальными, если от центра – центральными.
Главным достоинством числовых характеристик, обуславливающих их широкое применение, является то, что будучи характеристиками з-нов распределения случайной величины сами они не являются случайными.
Наиболее распространенной мерой рассеяния или неопределенности являтся 2-ой центральный момент з-на распределения, называемый дисперсией: 
. Свойство дисперсии: дисперсия суммы или разности независимых случайных величин равна соответственно сумме и разности дисперсий.
В метрологии вместо дисперсии обычно используется среднеквадратическое отклонение:
. Главным достоинством среднеквадратического отклонения является то, что оно имеет ту же самую размерность, что и измеряемая величина, поэтому их можно рассмотреть на одном графике.
При нормальном з-не распределения распространение вероятности попадания отсчета в определенный интервал можно рассчитать:
Вероятность отклонения отсчета на величину 
при нормальном з-не распределения определяется данной кривой. Интервал
[x-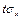 
; x+ 
] является доверительным интервалом и также может использоваться в качестве меры неопределенности отсчета. Величина интервала 2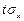 
зависит от выбора доверительной вероятности.
Если при многократном измерении физ. вел. сомнительное значение результата измерения отличается от среднего значения больше, чем на 3σ, то с вероятностью 0, 997 оно является ошибочным и его следует отбросить – правило 3-х σ .
|
|
|
|
|
|
