Главная | Обратная связь | Поможем написать вашу работу!

Основы микропроцессорных. Систем управления. Комсомольск-на-амуре 2002. Егоров В. А.

Министерство образования Российской Федерации

Государственное образовательное учреждение высшего профессионального образования «Комсомольский - на - Амуре государственный технический университет»

Институт дистанционного образования

В. А. Егоров

ОСНОВЫ МИКРОПРОЦЕССОРНЫХ

СИСТЕМ УПРАВЛЕНИЯ

Ученым советом Государственного образовательного учреждения высшего профессионального образования «Комсомольский - на - Амуре государственный технический университет»

Комсомольск-на-Амуре 2002

УДК 681. 325. 5-181. 4(075)

ББК 32. 973. 26я7

Е 302

Егоров В. А.

Е 302 Основы микропроцессорных систем управления: Учебно-методическое пособие. Комсомольск-на-Амуре: Государственное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет», 2002. – 61 с.

Кратко изложены вопросы аппаратной организации основных узлов цифровой микросхемотехники, необходимые для успешного освоения микропроцессорной техники и её использования в управляющих системах.

Предназначено для студентов заочной формы обучения.

ББК 32. 973. 26я7

ВВЕДЕНИЕ

Бурное развитие технологий изготовления цифровых интегральных схем, характерное для конца двадцатого века, привело к появлению микропроцессоров (процессоров выполненных на одном кристалле кремния), а затем и однокристальных микроЭВМ. Малогабаритные и недорогие (от одного доллара США) эти устройства стали широко использоваться при реализации электронных схем, всё более и более тесня своих аналоговых собратьев. В результате на сегодняшний день трудно найти современную систему управления, выполненную на базе аналоговых электронных элементов. МикроЭВМ встраиваются в бытовую технику, автомобильную технику и даже в игрушки. Управляющие системы на производстве организованы в иерархические вычислительные сети с суперЭВМ на верхнем уровне и локальными управляющими контроллерами – на нижнем.

Такое положение вещей не могло не привести к соответствующей корректировке программы обучения специалистов по автоматизации технологических процессов и производств. В программе появились курсы, знакомящие: с цифровой микросхемотехникой; принципами организации и функционирования микропроцессорных систем; дающие навыки программирования и практического использования микропроцессоров. К ним и относится данный курс «Основы микропроцессорных систем управления».

Микропроцессорная система управления или микроконтроллер представляет собой совокупность программно-аппаратных средств, поэтому специалист по цифровым системам управления – это, прежде всего, специалист по программированию и цифровой электронике. Этим и обусловлен круг вопросов, рассматриваемых в данном пособии. В главах один и два рассмотрены способы представления и кодирования информации в ЭВМ. В третьей главе изложены математические основы построения цифровых схем (алгебры Буля). Четвертая глава посвящена описанию типовых узлов цифровой микросхемотехники. В пятой главе рассмотрены принципы организации микропроцессоров.

Таким образом, данный курс является вводным в блоке дисциплин, посвящённых использованию микропроцессоров в системах управления, и содержит сведения об аппаратных средствах.

Хотелось бы выразить благодарность людям, в разное время работавшим на кафедре ЭПиАПУ КнАГТУ и участвовавшим разработке базовой концепции данного курса и учебно-методического обеспечения - доцентам Прокопову А. А. и Мурашко Ю. П., а также студентам специальности 210100 «Управление и информатика в технических системах», внесших посильный вклад в проработку отдельных вопросов и создание рукописи, и в частности Урасову Д.

Автор

1. СИСТЕМЫ СЧИСЛЕНИЯ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВ

1. 1. Понятие о позиционных системах счисления

Под системой счисления понимается способ представления любого числа посредством некоторого алфавита символов, называемых цифрами. Существуют различные системы счисления.

Римская система счисления является примером очень сложного способа записи чисел и имеет громоздкие правила арифметических действий. Число 35 в этой системе счисления будет записываться: ХХХУ. Такая система счисления называется непозиционной, так как цифрыздесь всегда имеют одно и то же значение независимо от того, на каком месте они стоят ( Х в римской системе счисления всегда обозначает десяток ).

Система счисления называется позиционной, если одна и та же цифра имеет различные значения, определяемые позицией цифры в последовательности цифр, изображающей число. Эти значения меняются в зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером такой системы счисления является десятичная система, используемая в повседневной жизни. В числе двести двадцать два – 222 крайняя справа двойка обозначает две единицы, в середине - два десятка, крайняя слева - две сотни.

Количество P различных цифр, употребляемых в позиционной системе, называется её основанием. Эти цифрыобозначают P целых чиселот 0 до P -1. В десятичной системеиспользуются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, следовательно, эта система имеет основанием число десять.

В общем случае в позиционной системе с основанием P любоечисло X может быть представлено в виде полиномаот основания P:

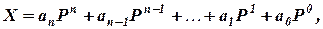(1)

где в качестве коэффициентов 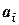могут стоятьлюбые из P цифр, используемых в системе счисления.

Принято представлять числа в виде последовательностисоответствующих выражению (1) цифр:

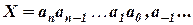
В этой последовательности запятая отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Запятая опускается, если нет отрицательныхстепеней. Позиции цифр, отсчитываемые от запятой, называют разрядами. В позиционной системе счисления значение каждого разряда больше значения соседнего справа разряда в число раз, равное основанию системы P.

С учетом сказанного, в десятичной системесчисления запись 6097. 108 означает число:

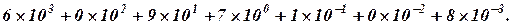
В цифровой автоматике и вычислительных машинах применяют позиционные системысчисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную. В дальнейшем дляобозначения используемой системы счисления будем заключать число в скобки и в индексе указывать основание системы счисления.

1. 1. 1. Двоичная система счисления

В двоичной системе счисления используются только две " двоичные" цифры: 0 и 1. Любое число в этой системе может быть представлено последовательностью двоичных цифр, что согласно (I) соответствует сумме степеней числа 2, взятых с коэффициентами, равными 0 или 1. Например:

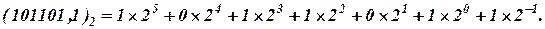
Вычисление этой суммы в десятичной системе счисления даёт десятичное значение числа .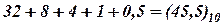

Применение двоичной системы счисления создает большие удобства при проектировании цифровых систем управления, обработки и передачи информации, так как для представления разряда двоичного числа может быть использован любой простой элемент, имевший всего два устойчивых состояния, например реле или триггерные схемы. Другим важным достоинством двоичной системы является простота двоичной арифметики, двоичные числа часто встречаются в технической литературе и могут использоваться в языках высокого уровня, таких, как «Си», «Паскаль» и т. д. Иногда для их отличия от чисел, представленных в других системах счисления, после цифр ставится буква В (от английского слова Binary). Например:

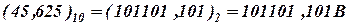
При программировании микропроцессоров и микроЭВМ часто возникает необходимость писать большие массивы двоичных чисел, но большое количество разрядов и однообразие символов служат источником ошибок программистов, поэтому для записи двоичных чисел широко применяются восьмеричная и шестнадцатеричная системы счисления. Основания этих систем кратны основанию двоичной системы счисления, что обеспечивает удобство преобразования из одной системы счисления в другую. Обычно это выполняется для целых чисел, поэтому дроби рассматривать в дальнейшем не будем.

1. 1. 2. Восьмеричная система счисления

В восьмеричной системе счисления используются восемь цифр: 0, 1, 2, 3, 4. 5, 6, 7. Любое число в восьмеричной системе представляется последовательностью этих цифр. Восьмеричное число также может быть представлено полиномом (1) с разложением по степеням основания 8. Например:

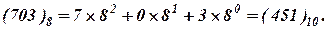
1. 1. 3. Шестнадцатеричная система счисления

В шестнадцатеричной системе для изображения чисел используют 16 знаков, которые изображаются десятью десятичными цифрами и шестью латинскими буквами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, С, D, E, F. Существуют и другие формы записи шестнадцатеричных цифр, но такая используется чаще. В этой форме - буквы используются для обозначения цифр, больших 9: А соответствует десятичному числу 10, В -десятичному числу 11, С - 12, D - 13, E - 14, F - 15. В шестнадцатеричной системе счисления любое число записывается последовательностью шестнадцатеричных цифр, и оно тоже может быть представлено полиномом ( 1) с разложением по степеням основания 16. Вычисление этого полинома в десятичной системе счисления позволяет получить десятичное значение данного числа. Например:

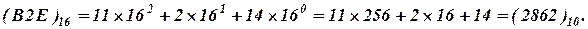
Для того чтобы отличать восьмеричные и шестнадцатеричные числа от записи чисел в других системах счисления, иногда используют буквенное обозначение. В конце восьмеричного числа добавляют букву Q (от английского octal), а в конце шестнадцатеричного числа букву Н (от английского hexadecimal). Например: число 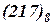может быть записано 217Q и число 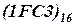может быть записано 1FC3H.

1. 2. Перевод чисел из одной системы счисления в другую

1. 2. 1. Перевод чисел из десятичной системы счисления в двоичную

В общем случае перевод целого числа из одной системы счисления в другую выполняется по следующему принципу: для перевода целого числа из Р -системы счисления в К -систему нужно последовательно делить это число и получаемые частные на основание К новой системы, представленное в старой Р -системе, до тех пор, пока частное не станет меньше К. Старшей цифрой в записи числа в К -системе служит последнее частное, а следующие за ней цифры дают остатки, выписываемые в последовательности, обратной их получению. Например, при переводе числа 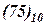в двоичную систему получим:

75½ 2

74 37½ 2

1 36 18½ 2

1 18 9 ½ 2

0 8 4 ½ 2

1 4 2 ½ 2

0 -2 1 (75)₁₀ = (1001011)₂

12 3 4 5 6 7 8 Следующая ⇒
Поделиться:

Воспользуйтесь поиском по сайту: