 |
(X + Y) + Z = X + (Y + Z); (X * Y) * Z = X * (Y * Z);
|
|
|
|
(X + Y) + Z = X + (Y + Z); (X * Y) * Z = X * (Y * Z);
Кроме того, в алгебре логики существуют законы, отличающиеся от законов обычной алгебры, и законы, свойственные только алгебре логики:
распределительный закон (дистрибутивность)
(X + Y) * Z = X * Z + Y * Z; X * Y + Z = (X + Z) * (Y + Z);
закон инверсии (правило де Моргана)
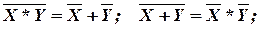
законы идемпотентности
X + X + … + X = X; X * X * … * X = X;
законы склеивания
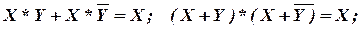
законы поглощения
X + X * Y = X; X * (X + Y) = X;
закон двойного отрицания

Для преобразования логических выражений полезно использовать следующие тождества:
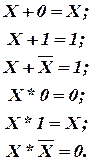
В справедливости этих законов и тождеств можно убедиться путем составления соответствующих релейных электрических схем и анализа их работы. При этом аргументы представляются замыкающими контактами, их инверсные состояния - размыкающими контактами, константы " 1 " и " 0 " представляются постоянным соединением и разрывом цепи соответственно, логическое умножение - последовательным соединением контактов, логическое сложение - параллельным соединением.
3. 5. Сложносоставные элементы цифровой микросхемотехники
На практике при создании схем дискретной автоматики и узлов ЦВМ удобнее использовать элементы, реализующие более сложные логические функции (рис. 7), из которых могут быть получены более простые элементы. Их условное обозначение определено стандартом, и в дальнейшем при изображении логических элементов и схем его необходимо придерживаться.
На рис. 7, а изображен элемент " И-НЕ ", выполняющий две функции: сначала логическое умножение, а затем инверсию. На рис. 7, б изображен элемент, выполняющий две функции: инверсию входов и логическое сложение сигналов, но по таблице истинности он является аналогом первого элемента. Такими же логическими аналогами являются элементы " ИЛИ-НЕ ", изображенные на рис. 7, в, г. На рис. 7, е приведен сложный элемент, включающий три двухвходовых элемента " И ", выходы которых соединены со входами элемента " ИЛИ-НЕ ", что поясняется на рис. 7, д. Такое изображение рекомендуется, когда элемент выполнен в одном корпусе микросхемы.
|
|
|

Рис. 7. Условное графическое обозначение сложных логических элементов
3. 6. Составление логических выражений по таблице истинности
Логическое выражение для функции может быть составлено по таблице истинности. Для этого необходимо составить логические произведения аргументов только для тех строк, в которых функция равна 1. Если аргумент в строке равен 0, то в произведении он берется с отрицанием, если аргумент равен 1, то без отрицания. Полученные произведения соединяются знаком логического сложения.
Например: в таблице истинности (см. табл. 3) функция равна 1 в пяти последних строках таблицы, значит надо составить пять произведений аргументов, соответствующих этим строкам, и соединить их знаком логического сложения:
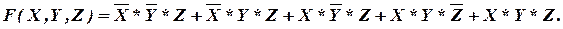
В дальнейшем это выражение может быть упрощено, для чего его надо преобразовать, используя законы алгебры логики. Добавим к исходному уравнению еще одно слагаемое X*Y*Z (согласно закону идемпотентности одинаковых слагаемых можно добавить сколько угодно) и сгруппируем члены уравнения:
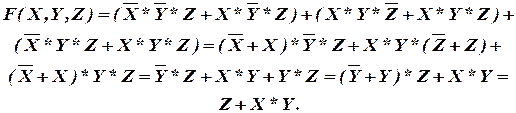
Такое же логическое выражение можно составить, анализируя непосредственно релейную схему (см. рис. 3), которой соответствует рассмотренная таблица истинности. В этой схеме ключи Х и Y соединены последовательно, и им параллельно подключен ключ Z.
3. 7. Составление логических выражений по бесконтактным схемам
Логическое выражение может быть составлено по схеме на бесконтактных логических элементах. Для этого, двигаясь от входов к выходу, проводят анализ преобразования сигналов на отдельных логических элементах. Пример такого анализа приведен на рис. 8.
|
|
|
Полученная на выходе логическая функция может быть в дальнейшем упрощена согласно законам алгебры логики.

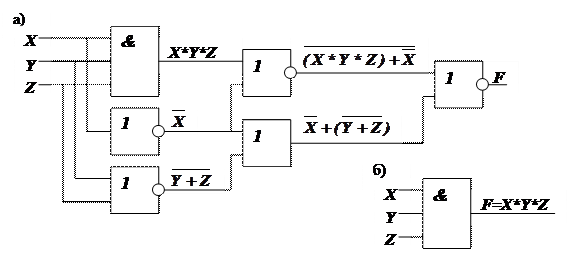
Рис. 8. Пример анализа схемы на логических элементах
Таким образом, исходная схема (рис. 8, а) является избыточной и её логическая функция может быть реализована одним логическим элементом (рис. 8, б). Алгебра логики является эффективным средством анализа и минимизации схем дискретной автоматики.
3. 8. Построение схем по логическому выражению
Построение схем по логическому выражению (синтез схем) начинают также с входов, при этом их количество равно количеству аргументов (каждый вход - это отдельный независимый сигнал-аргумент). Затем последовательно ставят логические элементы, которые будут преобразовывать поступающие сигналы согласно приоритету логических операций в исходном логическом выражении. Например, для выражения  схема будет иметь вид, представленный на рис. 9.
схема будет иметь вид, представленный на рис. 9.

Рис. 9. Пример синтеза схемы на логических элементах
3. 9. Составление таблицы истинности по логическому выражению
Составление таблицы истинности по логическому выражению заключается в подстановке значений аргументов для данной строки таблицы в логическое выражение и его вычислении. Например, для выражения  в строке, где Х = 0 и Y = 1, получаем
в строке, где Х = 0 и Y = 1, получаем
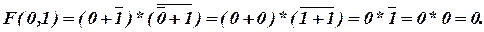
Полученный результат записывается в столбец значений функции. Такие вычисления выполняют для каждой строки (напоминаем, что при n - аргументах таблица истинности будет иметь 2n строк).
3. 10. Вопросы для повторения
1. Дайте определения понятию логические переменные. Приведите технические и другие примеры явлений, которые описываются логическими переменными.
2. Назовите три основные логические операции. Каков приоритет этих операций в сложных логических выражениях?
3. Каково назначение таблицы истинности и сколько в ней строк?
4. ТИПОВЫЕ УЗЛЫ ЦИФРОВОЙ МИКРОСХЕМОТЕХНИКИ
4. 1. Комбинационные схемы
4. 1. 1. Понятие о комбинационной схеме
Комбинационная схема – это устройство цифровых систем, у которых совокупность выходных сигналов в дискретный момент времени определяется входными сигналами, поступившими на входы в тот же дискретный момент времени. Реализуемый в этих схемах способ обработки информации называется комбинационным, так как результат обработки зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
|
|
|
Закон функционирования комбинационной схемы определен, если задано соответствие между входом и выходом, например в виде таблицы или в аналитической форме в виде логического выражения.
4. 1. 2. Схема совпадения кодов
В качестве примера комбинационной схемы рассмотрим схему совпадения двух двоичных сигналов, которая реализует логическую функцию двух переменных, называемую «эквивалентность». Эта функция равна 1, если входные сигналы совпадают, и равна 0, если не совпадают. Таблица истинности этой функции F отражает зависимость её от значений входных переменных X и Y (табл. 7).
Таблица 7
| X | Y | F(X, Y) |
Запишем логическое выражение. Для этого по табл. 8 составим логическую сумму, где слагаемыми являются логические произведения аргументов, взятых из строк, где функция равна 1. При этом если в этой строке аргумент равен 0, то он берется с инверсией. В данном случае F равна 1 в первой и последней строке, причем в первой строке оба аргумента равны нулю. Поэтому логическое выражение имеет вид:
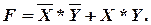

Для аппаратной реализации логических выражений используем бесконтактные логические элементы, при этом учитываем правило приоритета: сначала выполняются действия в скобках (в данном случае их нет), затем операции логического отрицания (инверсии), далее выполняется логическое умножение и последним логическое сложение. Такая последовательность операций для нашего выражения дает схему (рис. 10).
Такие схемы используются для контроля точного совпадения двоичных кодов, при этом количество таких схем равно разрядности кодов, а выходы схем объединяются на элементе И.
|
|
|

Рис. 10. Схема совпадения (эквивалентность)
4. 1. 3. Дешифратор
Дешифратор - это комбинационная схема, имеющая n входов и m выходов и преобразующая комбинацию входных сигналов (код) в выходной сигнал на отдельном выходе, номер которого является десятичным эквивалентом двоичного кода на входе. То есть каждому предусмотренному набору входных сигналов соответствует один вполне определенный возбужденный выход. Дешифратор называется полным, если он имеет столько выходов m, сколько различных комбинаций может иметь n – разрядное двоичное число на его входах, то есть m = 2n.
Если дешифратор имеет три входа, то максимально он будет иметь восемь выходов. Все состояния такого дешифратора приведены в табл. 8.
Таблица 8
|
Входы |
Выходы | |||||||||
| X2 | X1 | X0 | P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 |
Аналитически его работа описывается логическими выражениями:
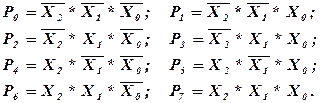
Согласно этим выражениям схема дешифратора на три входа имеет вид, изображённый на рис. 11.
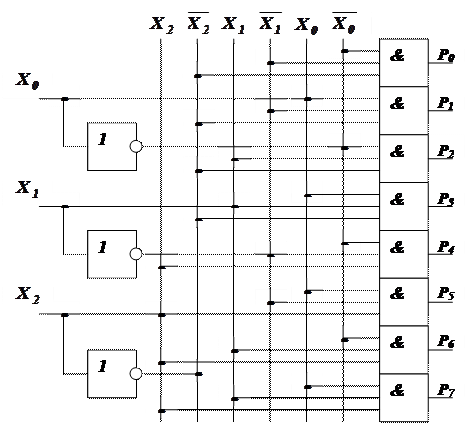
Рис. 11. Схема полного дешифратора на три входа
Дешифратор широко применяется в цифровых устройствах в системах преобразования сигналов и выбора элементов, поэтому он выпускается в виде отдельной микросхемы. Следует также отметить, что дешифратор может имнеть дополнительные вспомогательные входы (например вход синхронизации или выбора микросхемы), которые расширяют возможности его использования. Дешифраторы имеют условное обозначение (рис. 12). Здесь дешифратор имеет дополнительный вход выбора микросхемы “CS”. При наличии на входе “CS” логического нуля, все выходы будут иметь состояние логического нуля, независимо от входной комбинации.

Рис. 12. Условное графическое обозначение дешифратора на три входа (3: 8)
4. 1. 4. Мультиплексор
Мультиплексор - это комбинационная схема, обеспечивающая выбор и подключение сигнала с одной из нескольких входных линий на выходную. Как правило, мультиплексор (его еще называют селектором) имеет n управляющих и m=2n информационных входов и один выход. На управляющие входы подается число в двоичном коде, которое указывает, какой из информационных входов подключить к выходу (какой из входных информационных сигналов передать на выход).
Например, мультиплексор с двумя управляющими входами ( n = 2 ) может иметь четыре информационных входа ( m= 2n ), и его работа описывается табл. 9, где X1 , X0 - управляющие входы, D3, D2, D1, D0 - информационные входы, Y - выход.
|
|
|
Таблица 9
| X1 | X0 | Y |
| D0 D1 D2 D3 |
В соответствии с табл. 9 логическое выражение, описывающее работу мультиплексора на четыре информационных входа, имеет вид:
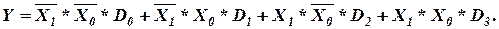
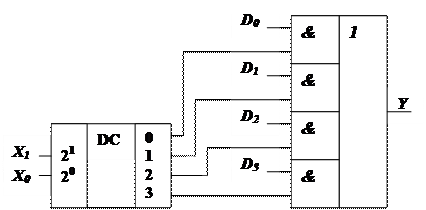
Рис. 13. Схема мультиплексора на четыре информационных входа
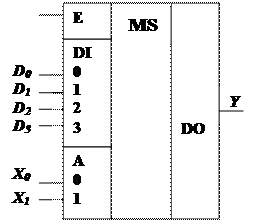
Рис. 14. Условное графическое обозначение мультиплексора
Согласно этому выражению схема мультиплексора может быть реализована следующий образом (рис. 13).
Дешифратор, как и мультиплексор, может иметь дополнительные управляющие входы, например вход синхронизации E. Условное графическое обозначение мультиплексора изображено на рис. 14.
4. 1. 5. Вопросы для повторения
1. Какое устройство называется комбинационной схемой?
2. Как задается закон функционирования комбинационной схемы?
3. Как составить логическое выражение по таблице?
4. Что учитывается при составлении схем по логическому выражению?
5. Какая схема называется дешифратором?
6. Какой дешифратор называется полным?
7. Какая схема называется мультиплексором?
8. Каково назначение управляющих и информационных входов?
9. Как обозначаются на схемах дешифраторы и мультиплексоры, если они выполнены отдельной микросхемой?
4. 2. Триггеры
4. 2. 1. Общие сведения о триггерах
Триггер – это простой цифровой автомат с памятью, то есть схема, состояние входов которой зависит не только от состояния входов в данный момент времени, но и от состояния самого устройства в предыдущие моменты времени.
Триггер является элементом, который может находиться в одном из двух устойчивых состояний. Одному из этих состояний приписывается значение 1, а другому 0.
Состояние триггера распознается по его выходу.
Под влиянием входного сигнала триггер скачкообразно переходит из одного устойчивого состояния в другое. При этом скачкообразно изменяется уровень напряжения его выходного сигнала.
Для удобства использования в схемах вычислительных устройств триггеры обычно имеют два выхода – прямой Q и инверсный 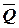 . В единичном состоянии триггера на выходе Q высокий уровень сигнала (логическая единица), а в нулевом состоянии - низкий (логический нуль), на выходе
. В единичном состоянии триггера на выходе Q высокий уровень сигнала (логическая единица), а в нулевом состоянии - низкий (логический нуль), на выходе 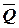 – наоборот. Существует несколько различных типов триггеров. Рассмотрим некоторые из них.
– наоборот. Существует несколько различных типов триггеров. Рассмотрим некоторые из них.
4. 2. 2. Асинхронный RS – триггер
Триггеры этого типа имеют два входа, обозначаемые буквами S (от английского set - установить) и R (от reset - сбросить) и используемые соответственно для установки триггера в единицу и ноль. Работа такого триггера описана в табл. 10.
Схема RS – триггера может быть получена из двух логических элементов ИЛИ-НЕ (см. рис. 15, а), соединенных таким образом, что возникают положительные обратные связи, благодаря которым в устойчивом состоянии выходной транзистор у одной схемы ИЛИ-НЕ закрыт, а у другой - открыт. При отсутствии сигналов на входах ( R=0, S=0 ) это состояние сохраняется сколько угодно долго, пока есть питание на схеме.
Таблица 10
| S | R | Q | Режим |
| х - | Хранение Запись 0 Запись 1 Комбинация запрещена |
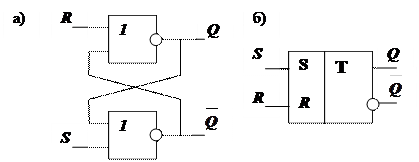
Рис. 15. Схема (а) и условное графическое обозначение (б) асинхронного RS – триггера на элементах ИЛИ-НЕ
При подаче сигнала на один из входов происходит подтверждение установки триггера или его переключение. При R=1, S=1 (запрещенный режим) оба выхода триггера устанавливаются в нулевое состояние и нельзя с определенностью сказать, в каком состоянии будет триггер после одновременного снятия входных сигналов. На рис. 15, б приведено условное обозначение асинхронного RS - триггера.
Часто триггеры этого типа реализуются на элементах И-НЕ (см. рис. 16, а); для них таблица переходов (табл. 11) и условное обозначение (рис. 16, б) будут иными.
Таблица 11

| 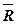
| Q | Режим |
| - х | Комбинация запрещена Запись 1 Запись 0 Хранение |

Рис. 16. Схема (а) и условное графическое обозначение (б) асинхронного RS – триггера на элементах И-НЕ
В отличие от предыдущего случая здесь управление триггером осуществляется подачей на один из входов логического нуля.
4. 2. 3. Синхронный RS – триггер
Для повышения надежности и более четкой работы цифровые устройства переключаются в фиксированные моменты времени, задаваемые тактовыми импульсами или импульсами синхронизации. Введение синхронизации для RS – триггера осуществляется установкой на входе двух элементов И-НЕ (рис. 17, а).
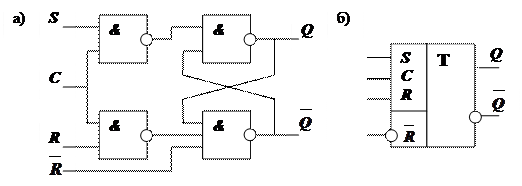
Рис. 17. Схема (а) и условное графическое обозначение (б) синхронного RS – триггера
В этой схеме вход C является входом синхронизации. При состоянии входа C = 0 оба входных элемента И-НЕ на своих выходах имеют единичное состояние и, следовательно, RS – триггер (вторая часть схемы) находится в состоянии хранения информации. Установка триггера в состояние 0 или 1 возможна только при подаче на вход C тактового импульса ( C = 1 ). Действительно, допустим, что на вход подано S = 0, R = 1, и с приходом тактового импульса верхний элемент будет иметь на выходе 1, а нижний – 0, что приведет к переводу триггера в нулевое состояние. По окончании тактового импульса триггер опять закроется и перейдет в режим хранения. При наличии импульсов синхронизации таблица переходов синхронного RS – триггера соответствует табл. 10.
4. 2. 4. Двухтактный RS – триггер
В некоторых случаях новое состояние триггера оказывается логически зависимо от состояния своего выхода. В этих случаях используют двухтактные схемы (рис. 18, а).
Двухтактный RS – триггер состоит из двух включенных последовательно синхронных однотактных триггеров, образующих две ступени. Причем вход синхронизации второй ступени подключен к входу синхронизации схемы через инвертор. Поэтому при отсутствии импульса синхронизации ( C = 0 ) входы схемы закрыты, а на вход C второй ступени подается 1, и она открыта, поэтому состояние первой и второй ступени одинаковое. При подаче импульса синхронизации ( C = 1 ) открывается первая ступень и закрывается вторая, что обеспечивает сохранение предыдущей информации до конца действия импульса синхронизации и прием новой информации на первую ступень. По окончании импульса синхронизации происходит закрытие первой ступени, открытие второй и перезапись новой информации с первой ступени на вторую. Следовательно, на выходе всей схемы устанавливается новая информация. Таким образом, в данной схеме информация заносится в два приема: сначала на первую ступень триггера, а затем на вторую. Наглядно это можно показать временной диаграммой (рис. 19).
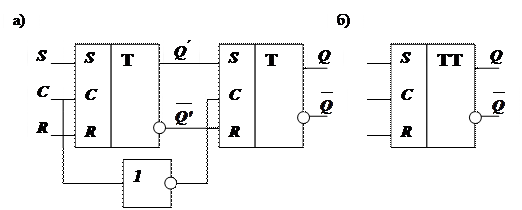
Рис. 18. Схема (а) и условное графическое обозначение (б) синхронного двухтактного RS – триггера
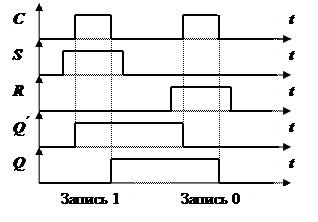
Рис. 19. Временная диаграмма работы двухтактного RS – триггера.
Из диаграммы видно, что в отличие от однотактных схем в двухтактных - информация устанавливается по заднему фронту импульса синхронизации. Это гарантирует отсутствие повторного изменения состояния схемы за один цикл синхронизации даже в том случае, когда входные сигналы через внешние цепи зависят от выходных.
На условном графическом обозначении (рис. 18, б) двухтактные триггеры обозначаются двумя буквами Т.
4. 2. 5. Универсальный JK-триггер
Общей особенностью RS - триггера является наличие запрещенного состояния на входах ( S =1, R=1 ), когда может возникнуть неопределенное состояние. В JK -триггерах этот режим соответствует инверсии (изменение на противоположное) его состояния, так называемому счетному режиму, так как триггеры с таким режимом применяются в счетчиках. Это достигается введением перекрестных обратных связей с выходов на входы через элементы “ И ” (рис. 20, а) для двухтактного RS - триггера.
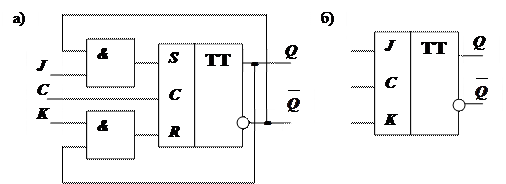
Рис. 20. Схема (а) и условное графическое обозначение (б) синхронного двухтактного JK – триггера
Для данной схемы в нулевом состоянии открыт вход J, а вход K закрыт, в единичном состоянии – наоборот. Таким образом, если на входы J и K будут одновременно поданы единицы, то действовать в течение одного цикла синхронизации будет только одна из них по отрытому входу, что обеспечивает перевод триггера в противоположное состояние. Работа JK - триггера соответствует временной диаграмме, представленной на рис. 21.
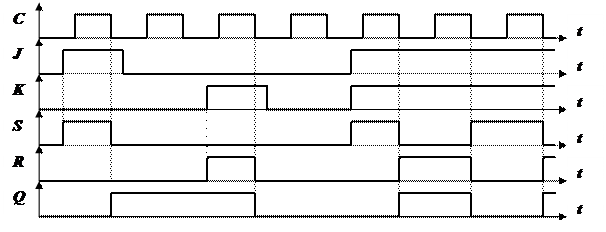
Рис. 21. Временная диаграмма работы JK –триггера
Состояния для JK – триггера ( при С=1 ) представлены в табл. 12, условное обозначение приведено на рис. 20, б.
Таблица 12
| J(S) | K(R) | Q | Режим |
| х x | Хранение Запись 0 Запись 1 Счётный |
JK-триггер удобен тем, что при различных вариантах подключения его входов можно получить схемы, функционирующие как RS-, D- и T- триггер, поэтому его ещё называют универсальным триггером.
4. 2. 6. Информационный D-триггер
Этот тип триггера имеет один информационный вход D и по импульсу синхронизации принимает состояние этого входа. D -триггер всегда имеет вход синхронизации и широко используется как запоминающий элемент при построении цифровых схем (в регистрах и блоках регистровой памяти). Он может быть реализован как на однотактном RS -триггере (рис. 22, а), так и на двухтактных RS и JK -триггерах (рис. 22). Здесь всегда вход S имеет состояние входа D, а вход R - противоположное состоянию D. Таким образом, для RS -триггеров в этих схемах есть только два режима: установки 0 и установки 1 (табл. 13).
При работе однотактные D -триггеры обеспечивают задержку одного сигнала на полцикла синхронизации (на время паузы), а двухтактные - на один цикл синхронизации. Условное обозначение D -триггера приведено на рис. 22, г.
Таблица 13
| D (S) | 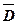 (R) (R)
| Q | Режим |
| Запись 0 Запись 1 |
Рис. 22. Схемы (а, б, в) и условное графическое обозначение (г) двухтактного
D – триггера
4. 2. 7. Счётный Т-триггер
У этого типа триггеров тоже только один информационный вход Т - счетный, и иногда есть дополнительные управляющие: синхронизации (или разрешение на счет), установки нуля и т. д. Этот триггер может быть построен на основе RS, JK или D -триггеров (рис. 23). При этом здесь только один режим - счетный.
На рис. 23 приведены схема построения несинхронного Т -триггера на основе RS и D -триггеров (рис. 23, а, в), а также схема синхронного Т -триггера на основе JK -триггера (рис. 23, б) и его условное графическое обозначение (рис. 23, г).

Рис. 23. Схемы (а, б, в) и условное графическое обозначение (г) T– триггера
Режим работы Т -триггера соответствует счетному режиму JK -триггера; с каждым импульсом на входе Т (при наличии импульса синхронизации) триггер меняет свое состояние на противоположное. Сказанное иллюстрирует временная диаграмма (рис. 24).
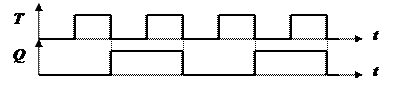
Рис. 24. Временная диаграмма работы T– триггера
Все схемы Т -триггера (рис. 23) имеют обратные связи с выхода на вход, поэтому Т -триггер может быть только двухтактным. Учитывая, что все двухтактные триггеры срабатывают по заднему фронту, становится понятным, почему моменты переключения совпадают со спадом импульса на входе Т (рис. 24).
Сопоставляя периоды входной и выходной частот на диаграмме (рис. 24) можно отметить эффект деления частоты на два.
Описанные свойства Т -триггера позволяют использовать его, как базовый элемент для построения счётчиков и делителей частоты.
4. 2. 8. Вопросы для повторения
1. Дайте определение понятию триггер.
2. Как определить состояние триггера?
3. Чем отличается работа асинхронного RS -триггера на элементах " И-НЕ " от RS -триггера на элементах '' ИЛИ-НЕ "?
4. Какие сигналы на входе необходимы для перевода синхронного RS -триггера в единичное состояние?
5. Чем отличается работа однотактного и двухтактного RS -триггера?
6. Составьте временную диаграмму работы для JK -триггера.
7. Чем отличается работа RS и D -триггера?
8. Составьте схему Т -триггера на основе D –триггера и поясните её принцип работы.
9. Составьте временную диаграмму работы Т -триггера.
4. 3. Регистры
Регистром называется устройство, предназначенное для запоминания многоразрядного двоичного слова, а также для выполнения над словом некоторых преобразований. Регистр представляет собой совокупность D –триггеров, число которых соответствует количеству разрядов в слове, и вспомогательных схем, обеспечивающих выполнение некоторых операций, среди которых могут быть: установка регистра в 0 (" сброс" ), приём слова из другого устройства (регистра, сумматора и т. д. ), передача слова в другой регистр, сдвиг слова вправо или влево на требуемое число разрядов, преобразование последовательного кода слова в параллельный и наоборот.
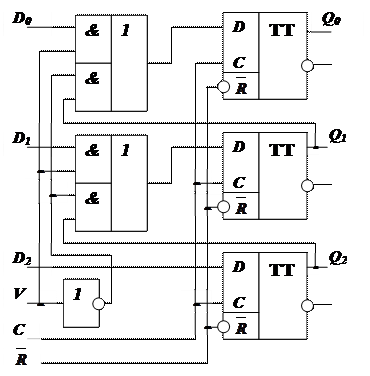
Рис. 25. Схема универсального трехразрядного регистра
На рис. 25 приведена схема трехразрядного регистра, позволяющая вводить и выводить информацию в последовательном и параллельном кодах, сдвигать слова по разрядам вправо, устанавливать регистр в 0. Регистр выполнен на трёх D -триггерах, имеет 3 информационных входа D2, D1, D0 и 3 выхода Q2, Q1, Q0, а также управляющие входы: 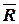 - установка нуля, С - синхронизации и V – задания режима работы.
- установка нуля, С - синхронизации и V – задания режима работы.
В рабочем состоянии на вход 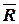 постоянно подается 1. При задании
постоянно подается 1. При задании  = 0 происходит установка всех триггеров в нулевое состояние, то есть сброс регистра в нуль.
= 0 происходит установка всех триггеров в нулевое состояние, то есть сброс регистра в нуль.
Для перевода регистра в режим параллельного ввода необходимо подать на вход V уровень логической единицы. При этом на верхние элементы " И " логических элементов " 2-2 И-ИЛИ " поступит 1, и они подключат к входам D -триггеров входы регистра D2, D1, D0.
Запись параллельного двоичного кода производится в следующем порядке. На входы D2, D1, D0 выставляют разряды кода. Подают импульс на вход синхронизации С. По окончании импульса (триггеры двухтактные) по его заднему фронту триггеры примут состояние входов, и информация будет записана.
Для последовательного ввода информации необходимо на вход V подать логический нуль, тогда нуль поступит на верхние элементы " И " и закроет их, отключая тем самым входы D -триггеров от входов регистра D2, D1, D0. В то же время, пройдя через инвертор, сигнал V откроет нижние элементы " И " и соединит входы D -триггеров с выходами предыдущих D -триггеров.
Теперь, чтобы ввести информацию, необходимо на вход D2 подать значение первого разряда вводимого кода, затем подать импульс синхронизации. На первом триггере установится значение первого разряда. Далее на вход D2 подают значение второго разряда и снова формируют синхроимпульс. При этом информация с первого триггера перепишется на второй, а на первом – установится значение вводимого второго разряда. Аналогично вводится третий разряд кода, при этом по окончании третьего импульса первый разряд кода запишется в первый триггер, второй разряд – во второй триггер, а третий (старший) разряд – в третий триггер. При последовательном вводе надо подавать столько импульсов, сколько разрядов в последовательном коде или триггеров в регистре (обычно их число совпадает).
Таким образом, при параллельном вводе информация вводится за один такт, но требуется n входов, где n - разрядность регистра (кода), а при последовательном вводе требуется n тактов, но всего один вход. Обычно параллельная передача информации применяется при коротких линиях связи (внутри вычислительных систем), а последовательная - при длинных линиях связи.
Считывание информации из регистра в параллельном коде осуществляется одновременным снятием сигналов с выходов Q2, Q1, Q0.
Считывание в последовательном коде выполняется с выхода Q0 в следующем порядке: с Q0 считывается значение первого разряда, подается импульс на вход С для сдвига информации по триггерам на один разряд, с выхода Q0 считывается значение второго разряда, затем снова подается импульс для сдвига, и опять считывание с Q0 значения третьего разряда. Для считывания n -разрядного числа необходимы n считываний и n сдвигов.
При сдвиге информация в регистре не сохраняется. Для сохранения информации необходим кольцевой сдвиг.
Регистр, выполненный в виде отдельной микросхемы, имеет следующее условное графическое обозначение на принципиальной схеме (рис. 26).
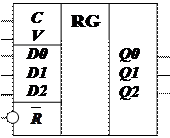
Рис. 26. Условное графическое обозначение регистра
4. 3. 1. Вопросы для повторения
1. Для чего предназначены регистры?
2. Какие операции выполняют регистры?
3. На каких элементах строятся регистры?
4. Чем отличается параллельный ввод информации от последовательного, в каких случаях они применяются?
5. Как считывается информация из регистра?
6. Какие регистры называются кольцевыми?
4. 4. Счётчики
Счетчик - это устройство, которое служит для подсчета количества импульсов, поступающих на его вход. По своему назначению счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующих счетчиках происходит сложение поступающих на вход импульсов с числом, которое хранится в счетчике. Вычитающие счетчики производят вычитание поступивших на вход импульсов из начального числа. Реверсивные могут как складывать, так и вычитать в зависимости от управляющего сигнала, который переключает счетчик либо в режим сложения, либо в режим вычитания.
Двоичные счетчики строятся на основе триггеров со счетным входом и дополнительных логических схем. Триггеры, входящие в счетчики, образуют его разряды. Максимально возможное число N , которое может быть зафиксировано счетчиком, называется его емкостью и для двоичных счетчиков определяется N = 2n - 1, где n - число разрядов.
Рассмотрим схему реверсивного счетчика (рис. 27), выполненного на трех JK -триггерах, работающих в счетном режиме.
На входы J и K всех триггеров подается логическая единица, которая задает счетный режим триггеров. Установка счетчика в нулевое состояние осуществляется подачей нулевого импульса по линии  , так как соответствующие входы триггеров - инверсные. В режиме счета
, так как соответствующие входы триггеров - инверсные. В режиме счета  = 1.
= 1.
Начальная установка двоичного числа в счетчик производится следующим образом. На вход P - " Счет" устанавливается уровень логического нуля, блокирующий счёт. Начальное число преобразуется в двоичный код и выставляется на входы D2, D1, D0 счётчика, являющиеся входами установки триггеров. Причём, младший разряд кода подается на вход D0.
Режим работы счетчика задается управляющим входом V. Если V = 0, то по линии " Вычитание" на верхние элементы " И " поступают 0, и они будут закрыты, а по линии " Сложение" будет поступать 1 на нижние элементы " И ", которые будут работать и передавать сигнал с инверсного выхода предыдущего триггера. Учитывая инверсию на выходе элемента " 2-2И-ИЛИ-НЕ ", получаем, что на вход С следующей ступени поступает сигнал, соответствующий состоянию предыдущего триггера.
В схеме используются двухтактные триггеры, которые срабатывают по заднему фронту синхроимпульса, то есть при переходе предыдущего триггера из единичного состояния в нулевое. Учитывая это, строим временную диаграмму для режима сложения (рис. 28). Первый триггер меняет свое сос
|
|
|


