 |
Основные элементарные функции
|
|
|
|
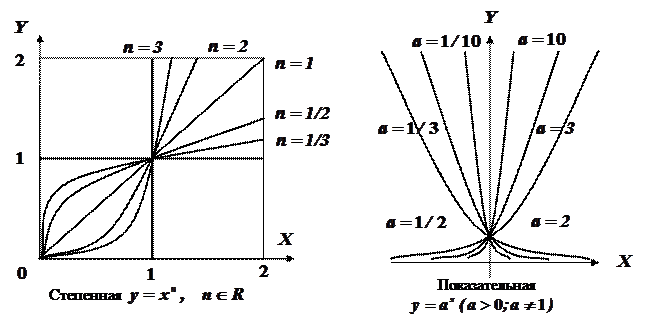
Элементарные функциями называют все функции, которые можно получить из основных элементарных с помощью алгебраических действий и образования сложных функций.
Предел числовой последовательности
Пусть каждому натуральному числу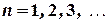 
по некоторому закону поставлено в соответствие действительное или комплексное число 
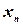. Тогда этим задана последовательность
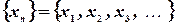
Отдельные числа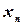 
последовательности 
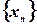называются ее элементами.
Надо иметь ввиду, что 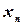и 
при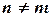 
считаются отличными как элементы последовательности, хотя не исключено, что как числа они равны между собой.
Определение. Число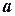 
называется пределом последовательности 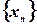, если для всякого 
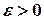найдется (зависящее от 
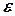) число 
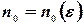такое, что выполняется неравенство
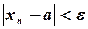
для всех (натуральных)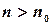 
.
В этом случае пишут
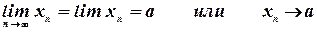
и говорят, что переменная 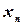или последовательность 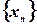имеет предел, равный числу 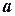, или стремится к 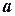. Говорят также, что переменная 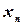или последовательность 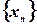сходится к числу .
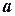Геометрический смысл предела
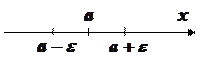Определение предела имеет следующий геометрический смысл: число 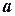является пределом последовательности 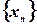, если в любой его 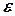- окрестности содержатся почти все члены 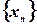, или вне этой окрестности находится лишь конечное число членов данной последовательности.
Пример 1. Дана последовательность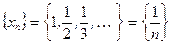 
. Предел этой последовательности 
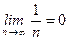, т.е. 
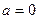. Действительно, зададим произвольное число 
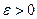и решим неравенство
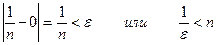
Этим для всякого 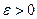найдено число 
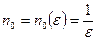такое, что неравенство 
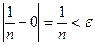выполняется для всех 
.
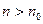Пример 2. Дана последовательность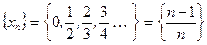 
. Предел этой последовательности 
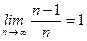, т.е. 
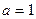. В самом деле, составим неравенство 
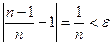. Оно, как мы видели, выполняется для любого 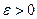, если 
.
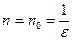Предел функции.
|
|
|
Число 
называется пределом функции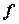 
в точке 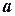, если она определена на некоторой окрестности 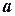, т.е. на некотором интервале 
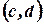, где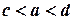 
, за исключением, быть может, самой точки 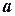, и если для всякого 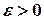можно указать зависящее от него 
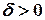такое, что для всех 
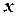, для которых 
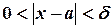, имеет место неравенство
.
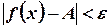Тот факт, что есть предел 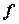в точке 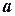, записывают следующим образом
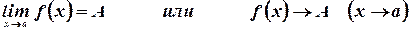
Выражение предел функции в точке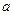 
часто заменяют выражением предел функции при 
, стремящемся к 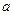, или, короче, предел функции при 
.
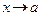По аналогии вводят следующее определение.
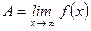
Число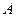 
есть предел функции 
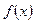при , стремящемся к бесконечности, если 
определена для всех , удовлетворяющих неравенству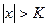 
при некотором 
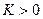, и для любого 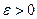можно найти число 
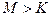такое, что 
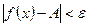для всех , удовлетворяющих неравенству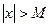 
.
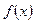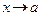Многие свойства пределов при , где 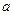- конечное число, и при 
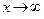являются аналогичными. Для этого под буквой 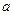либо число (конечное), либо символ 
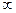. Если 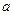есть число, то под окрестностью точки 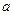понимается любой интервал 
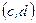, содержащий в себе точку 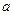. Таким образом, окрестность (конечной) точки 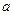есть множество всех точек , удовлетворяющих неравенствам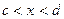 
. Если же 
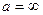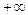(или 
или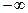 
), то под окрестностью 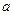условимся понимать множество всех , удовлетворяющих неравенству
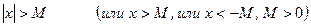
Произвольную окрестность точки 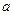обозначают символом 
.
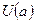Свойства пределов функции.
1. Если
и на некоторой окрестности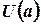 
, 
, 
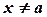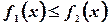, то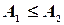 
.
2. Если
и на некоторой окрестности , ,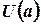 
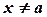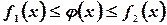, то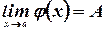 
.
3. Пусть 
, где и 
- конечные числа. Тогда
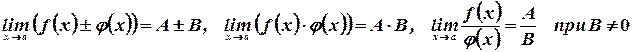
Признаки существования пределов
Теорема 1. Если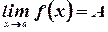 
, где - конечное число, то на некоторой окрестности 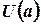функция 
ограничена, т.е. существует положительное число 
такое, что
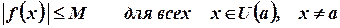
Теорема 3. (критерий Коши существования предела). Для того чтобы существовал предел (конечный)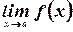 
, необходимо и достаточно, чтобы функция была определена в окрестности 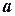, за исключением, быть может, самой точки 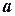, и для всякого 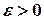существовала такая окрестность 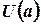, что, каковы бы не были точки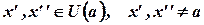 
|
|
|
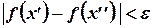
Односторонние пределы
По определению число называется пределом функции 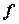в точке 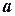справа (слева), если она определена на некотором полуинтервале 
(
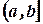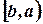) и для нее существует
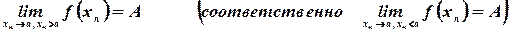
для любой указанной последовательности .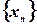
Предел справа (слева) функции 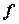в точке 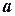принято обозначать так:
Если 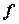определена на интервале 
, то в точке 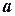может иметь смысл только число 
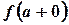, а в точке 
- только число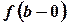 
.
Равенства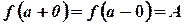 
эквивалентны существованию предела .
|
|
|
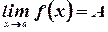