 |
Теоремы о непрерывных функциях
|
|
|
|
Функция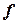 
называется непрерывной на отрезке 
, если она непрерывна во всех точках интервала 
, непрерывна справа в точке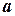 
и непрерывна слева в точке 
.
Теорема 5. Если функция 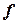непрерывна на отрезке , то она ограничена на нем, т.е. существует константа 
такая, что выполняется неравенство
На рисунке изображен график непрерывной функции 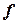на отрезке . Очевидно, что существует такое число , что график находится ниже прямой 
, но выше прямой 
.
Теорема 6 (Вейерштрассе). Если функция 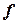непрерывна на , то существует ее минимум и максимум на , т.е. существуют точки 
такие, что 
для всех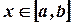 
. См. рис.
Теорема 7. Если функция 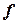непрерывна на отрезке и числа 
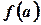и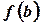 
не равны нулю и имеют разные знаки, то на интервале имеется 
по крайней мере одна точка 
такая, что 
.
Следствие 1. Если функция 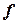непрерывна на , 
, 
, 
и 
произвольное число, находящееся между числами 
и 
, то на интервале найдется по крайней мере одна точка 
такая, что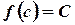 
.
Следствие 2. Непрерывная на отрезке функция принимает все промежуточные значения между ее наименьшим и наибольшим значениями.
9. Производная функции.
Пусть функция 
определена в окрестности 
. Тогда производной от функции в точке 
называется предел
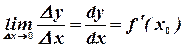
где 
. Функция, которая имеет производную, называется дифференцируемой.
Теорема 8 (о непрерывности дифференцируемой функции).
Если функция дифференцируема в 
, то она непрерывна в этой точке.
Доказательство.
Пусть существует производная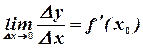 
. Тогда
,
причем 
. Отсюда
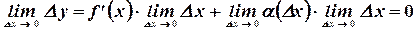
Отсюда следует, что значение 
непрерывно.
10. Основные правила дифференцирования.
1. 
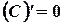
Доказательство:
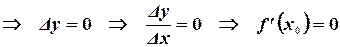
2. 
(производная от суммы равна сумме производных).
Доказательство: 
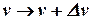
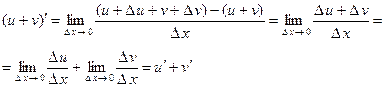
3. 
константу можно выносить за знак производной.
|
|
|
Доказательство: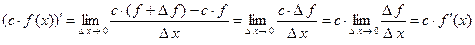 
Производная сохраняет линейные комбинации.
4. Производная произведения:
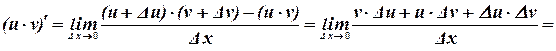
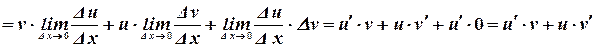
5. Производная частного:
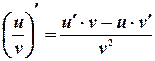
Доказательство:
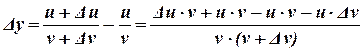
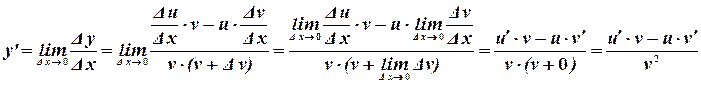
6. Производная сложной функции:
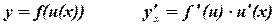
Доказательство:
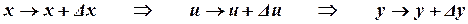
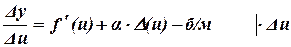
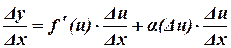
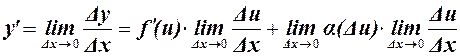
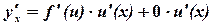
Пример.
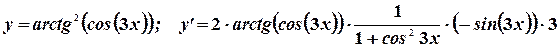
7. Производная обратной функции
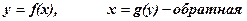
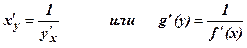
8. Производная функции, заданной параметрически:
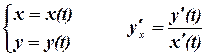
Доказательство: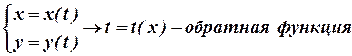 
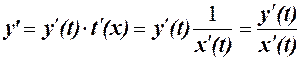
9. Производная функции 
. 
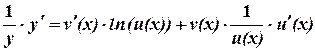
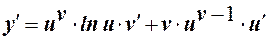
Пример. 
.
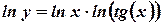
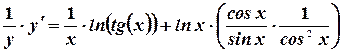
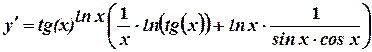10. Если функция задана неявно, т.е. уравнением 
, то производная 
этой неявной функции может быть найдена из уравнения 
, где рассматривается как сложная функция переменной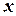 
.
Пример. Найти производную неявной функции 
.
Это уравнение определяет 
- функцию от . Подставляя функцию в данное уравнение, получаем тождество 
. Дифференцируем это тождество и из полученного уравнения находим .
.
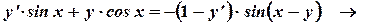
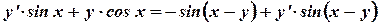
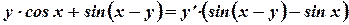
Производные элементарных функций
1. 
, 
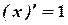
2. 
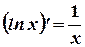
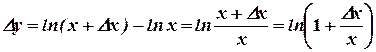
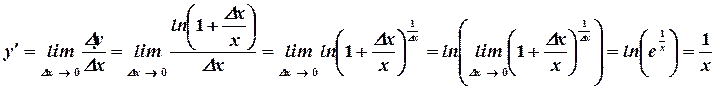
3. 
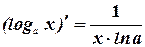
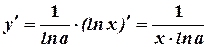
4. 
, 
, 
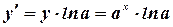
5. 
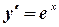
6. 
, 
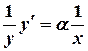
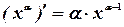
7. 
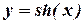
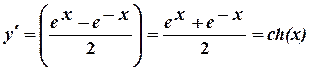
8. 
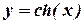
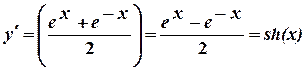
9. 
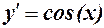
10. 
11. 
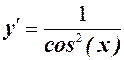
12. 
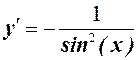
13. 
, 
14. 
, 
?
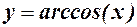15. 
, 
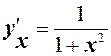
16. 
, 
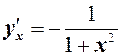
12. Геометрический смысл производной, уравнение касательной и нормали к кривой.
Пусть 
- фиксированная точка, 
- текущая, 
- секущая. При 
секущая переходит в касательную в точке (предельное положение секущей).
если 
то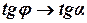 
.
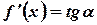Далее, нам известно уравнение прямой линии
Здесь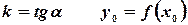 
. Отсюда
- уравнение касательной
- уравнение прямой, перпендикулярной данной.
- нормали.
Производные высших порядков явно заданных функций
Производной второго порядка, или второй производной, функции называется производная от ее производной 
.
Обозначение второй производной
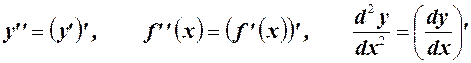
Аналогично определяются и обозначаются производные третьего, четвертого и более высоких порядков
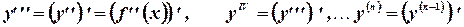
Производные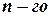 
порядка обозначаются и так
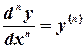
Если функция задана параметрически: 
, 
, то ее вторая производная определяется формулой
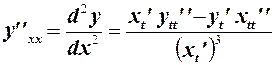
Дифференциал функции.
Пусть функция определена в окрестности и имеет производную в этой точке
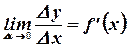
При этом 
. Тогда для достаточно малых 
можно записать
|
|
|
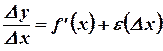
Причем 
при 
. В этом случае приращение функции можно записать в виде
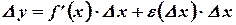
Или
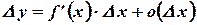
Определение. Функция 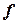называется дифференцируемой в точке 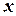, если ее приращение 
можно представить в виде
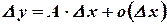
где не зависит от , но вообще зависит от .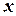
Теорема 9. Для того чтобы функция 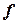была дифференцируема в точке 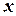, необходимо и достаточно, чтобы она имела конечную производную в этой точке.
Таким образом, сказать, что 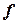имеет производную в точке 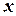или что 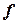дифференцируема в точке 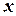- это одно и то же. Поэтому процесс нахождения производной называют дифференцированием функции.
Доказательство.
Достаточность условия доказана выше: из существования конечной производной 
следовала возможность представления 
в виде 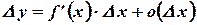, где можно положить 
.
Необходимость. Пусть функция 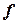дифференцируема в точке 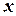. Тогда, если 
, можно записать
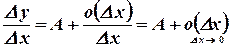
Предел левой части при существует и равен :
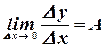
Это означает, что существует производная 
.
Геометрический смысл дифференциала.
Итак, приращение функции можно представить в виде
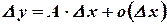
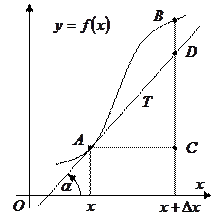Первое слагаемое 
пропорционально , т.е. оно - линейная однородная функция от . Второе, 
является бесконечно малой высшего порядка малости 
, т.е. оно стремится к нулю быстрее, чем первое. В связи с этим первое слагаемое 
называется главным членом приращения 
(при 
). Это слагаемое называют дифференциалом функции и обозначают символом 
. Итак, по определению
На рисунке - 
касательная к кривой в точке , 
, приращение функции 
соответствует приращению аргумента . При этом
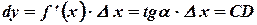
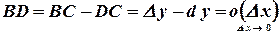
Вообще говоря 
. Равенство выполняется только для линейной функции. В этом случае дифференциал и приращение независимой переменной равны между собой 
. Поэтому дифференциал произвольной функции записывают обычно так
|
|
|
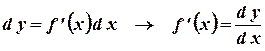
