 |
48) Построение графиков. Отделение корней. Решение алгебраических уравнений.
|
|
|
|
Mathcad предоставляет широкие возможности для построения и форматирования разных типов графиков – двумерных графиков в декартовых и полярных координатах, графиков поверхностей и карт линий уровня, векторных полей, трехмерных гистограмм и др. Графические объекты располагаются в графических областях, которые создаются автоматически при выполнении соответствующих команд меню Графика. График в декартовой системе координат в Mathcad представляет собой незаполненный шаблон в виде большого прямоугольника с темными маленькими прямоугольниками, расположенными около осей абсцисс и ординат будущего графика. В средние прямоугольники надо поместить имя аргумента x оси абсцисс и имя функции у оси ординат. Если в Mathcad строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние темные маленькие прямоугольники служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то в Mathcad масштабы по осям графика будут устанавливаться автоматически. Но автоматические масштабы могут оказаться не вполне удобными. Поэтому рекомендуется вначале использовать автоматическое масштабирование, а затем изменять их на более подходящие.
Чтобы произошло построение графика в автоматическом режиме вычислений в Mathcad, достаточно вывести курсор за пределы графического объекта. Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др. ) проще всего изменить, щелкнув дважды по полю графика. В результате активизируется диалоговое окно “Форматирование”, на котором в Mathcad выбирается соответствующая вкладка и устанавливаются параметры настройки графика. Возможно отображение на одном шаблоне графиков функций от различных переменных. В этом случае, количество переменных и функций, их имена и порядок следования должны быть синхронизированы.
|
|
|
В ходе численного решения обычно выделяют два этапа:
· отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
· уточнение корней – нахождение численного значения корня с указанной точностью.
Задание 1. Решить уравнение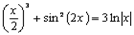 
.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
· Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
· Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например: x: =-5, -4. 9.. 5
· Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
· Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
· Для появления графика щелкнем левой клавишей мыши вне графической области.
· Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика ( Crossed – Только оси), добавим вспомогательные линии по координатным осям ( Grid Lines – Вспомогательные линии). Отменим при этом автосетку ( Autogrid – Автосетка) и установим количество линий сетки, равное 10.
· Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
|
|
|
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение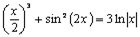 
имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2, 5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
x: =-1 TOL: =0. 0001
Уточним заданное приближение к значению корня с помощью функции root:
x1: =root(f(x), x)
x1=-1. 1395
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
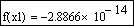
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить: 
Для решения уравнений в системе MathCad существует несколько способов.
· Если необходимо найти корень уравнения на заданном промежутке, можно воспользоваться функцией root c 4 аргументами: root(f(x), x, a, b), где f(x) - функция, определяющая уравнение, x - переменная, a и b - границы интервала на котором ищем корень. Пример: f(x): =x4 +9x3 +31x2 +59x+60 root(f(x), x, -5, -3)=-3
· Сокращенный вариант функции root - root(f(x), x), где f(x) - функция, x - первое приближение к корню. f(x): =x4 +9x3 +31x2 +59x+60 x: =10 root(f(x), 10)=-3
· Известно, что полином имеет максимум n корней, где n - это наибольшая степень полинома. f(x): =x4 +9x3 +31x2 +59x+60 Выпишем все коэффициэнты при x в обратном порядке, следующим образом: V0: =60 V1: =59 V2: =31 V3: =9 V4: =1 Затем выполним следующую команду: polyroots(V)= В результате выведетсяматрица корней уравнений
· Записываем уравнение следующим образом x4 +9x3 +31x2 +59x+60 Выделяем переменную x в любом месте выражения. В Меню Символы выбираем Переменные затем Вычислить. В итоге получим матрицу корней уравнения.
· С помощью оператора solve, который вводится с рабочей панели Символы, можно решать нелинейные уравнения и неравенства. В левый маркер вводится уравнение или неравенство, а в правый переменнай. Пример: x-1=0 solve, x → 1
|
|
|
