 |
52) Вычисление определенных интегралов.
|
|
|
|
52) Вычисление определенных интегралов.
Интеграл в Mathсad можно вычислить с помощью оператора интегрирования на панели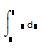 
. В результате активизируется шаблон определенного интеграла, который имеет четыре поля для ввода пределов интегрирования, переменной интегрирования и функции интегрирования. Результат вычисления определенного интеграла отображается после ввода знака равно “ = ”. При вычислении определенного интеграла для получения более точного и достоверного результата можно выбрать метод расчета путем вызова контекстного меню щелчком правой кнопки мыши по полю шаблона. По умолчанию активизирован режим “автовыбор”, при котором Mathcad автоматически выбирает один из методов.
· Метод Romberg (Ромберг) используется в Mathcad как общий метод для гладких функций;
· Adaptive (адаптивный) – для функций быстроизменяющихся на участке интегрирования;
· Infinie Limit (неограниченный лимит) – бесконечный предел – для расчета интегралов с бесконечными пределами интегрирования.
· Метод Singular Endpoint (сингулярный конец) применяется для расчета интегралов от функций, не существующих в одной или обеих точках пределов интегрирования (так называемые несобственные интегралы второго рода).
При необходимости пользователь может отказаться от режима “ автовыбор ” и принудительно указать в Mathcad нужный метод расчета. На листинге приведены примеры вычисления определенного интеграла. Как показывает анализ результатов расчета, режим автовыбор является наиболее универсальным при расчете определенного интеграла.
53) Метод наименьших квадратов. Обработка экспериментальных данных в системе компьютерной математики MATHCAD.
|
|
|
При анализе данных распространена следующая ситуация:
· Нам известен набор значений {xi, yi}, i=1, 2, …, N, отражающий общий характер исследуемой зависимости, но эти значения получены с погрешностями. Погрешности могут быть связаны с неточными измерениями, случайными или систематическими ошибками измерительных приборов, неверной интерпретацией данных человеком и т. п.;
· Из физических или математических соображений нам известен также общий характер (порядок) зависимости, например, первый (линейная зависимость, все точки yi должны лежать на одной прямой), второй (квадратичная зависимость, через точки следует провести параболу) и т. д. Обозначим порядок зависимости как M, при M=1 получается прямая, при M=2 – парабола, а в общем случае M может принимать значения 1≤ M< N.
Чтобы устранить действие погрешностей, нам требуется построить зависимость ϕ (x) порядка M, которая наилучшим образом приближает имеющиеся данные. Под наилучшим будем понимать такое приближение, при котором сумма отклонений ϕ (xi) от известных значений f(xi) минимальна:
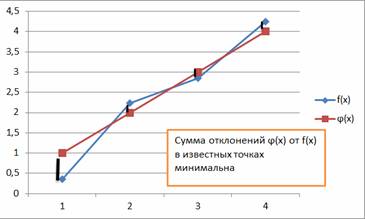
Чтобы не зависеть от знаков отклонений, будем учитывать их квадраты. Таким образом, искомая зависимость строится из условия минимума функционала 
Так как ищется минимум суммы квадратов отклонений, данный расчёт называют методом наименьших квадратов (МНК).
Существует несколько способов построения функционала МНК, например, такой:
• Определить порядок МНК m и исходные данные {xi, yi }, i=1, 2, …, n;
• Построить матрицу A размерностью n*(m+1) с элементами вида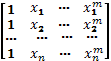 
;
• Транспонировать матрицу A, получив матрицу AT размерностью (m+1)*n;
• Вычислить произведение матриц Z=AT*A, размер матрицы Z равен (m+1)*(m+1);
• Вычислить вектор b из m+1 элементов по формуле b=AT*y, где вектор y содержит значения yi;
• Найти решение системы уравнений Z*c=b в виде c=Z-1*b, вектор c содержит m+1 элементов;
• В произвольной точке x функционал МНК может быть вычислен по формуле ϕ (x)=c0+c1*x+…+cm*xm
|
|
|
Задание: построить МНК 1 порядка по следующим значениям {xi, yi}:
| i | |||||
| xi | 1. 5 | 2. 5 | 5. 5 | ||
| yi | -1 |
Вывести на графике полученную зависимость f(x) и исходные данные {xi, yi}, границы графика по оси Ox принять от 0 до 7.
|
|
|
