54) Решение систем линейных уравнений методом Крамера.

54) Решение систем линейных уравнений методом Крамера.

В Mathcad метод Крамера также предназначен для решения системы n линейных уравнений с n неизвестными вида A*x =b на основе предварительного вычисления определителей системы, при условии, что определитель 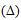матрицы А отличен от нуля. Метод основан на формулах Крамера, вида , где 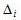– определитель матрицы, полученной из матрицы А системы заменойi –го столбца, т. е. столбца коэффициентов при неизвестном Xi вектором свободных членов, т. е. b. На листинге в Mathcad приведен пример решения системы линейных алгебраических уравнений методом Крамера.

55) Решение систем линейных уравнений. Транспонирование матриц, вычисление обратной матрицы и определителя.

См вопрос 50

Как известно, при транспонировании матрицы ее строки становятся столбцами. В mathcad есть функция, которая позволяет выполнить транспонирование. Введите имя матрицы, которую хотите транспонировать, и на панели Matrix нажмите кнопку " Matrix transpose". На рис. 4 смотрите синтаксис для записи этой операции.

Как известно, обратной матрицей M^-1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку " Invers". на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы

Определитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) или набрать на клавиатуре [|](нажав клавиши < Shift> +< \> ). В результате любого из этих действий появляется место заполнитель, в который следует поместить матрицу.