 |
Эквивалентная динамическая радиальная нагрузка
|
|
|
|
Для радиальных шарикоподшипников из условия равновесия вала следует:  ,
,  . Дальнейшие расчеты выполняем для более нагруженного подшипника опоры 2.
. Дальнейшие расчеты выполняем для более нагруженного подшипника опоры 2.
Отношение
 ,
,
где  .
.
В соответствии с табл.7.3 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов) имеем:  .
.
Коэффициент осевого нагружения согласно табл.7.2 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов):
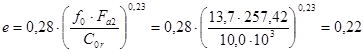 .
.
Отношение  , что меньше
, что меньше  (
( при вращении внутреннего кольца). Окончательно принимаем согласно табл.7.2 [Глава 7] (уч..Ф. Дунаев, О.П. Леликов):
при вращении внутреннего кольца). Окончательно принимаем согласно табл.7.2 [Глава 7] (уч..Ф. Дунаев, О.П. Леликов): 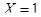 ,
,  .
.
Принимаем согласно табл.7.6 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов)  ;
; 
 .
.
Эквивалентная динамическая радиальная нагрузка:
 .
.
Расчетный ресурс подшипника
Расчетный скорректированный ресурс подшипника при  (вероятность безотказной работы 90%),
(вероятность безотказной работы 90%),  (обычные условия применения),
(обычные условия применения),  (шариковый подшипник):
(шариковый подшипник):

Расчет подшипников на промежуточном валу
Исходные даные:
ü частота вращения вала -  ;
;
ü делительный диаметр шестерни тихоходной ступени -  ;
;
ü делительный диаметр колеса быстроходной ступени -  ;
;
ü осевая сила, действующая на шестерню -  ;
;
ü радиальная сила, действующая на шестерню -  ;
;
ü окружная сила, действующая на шестерню -  ;
;
ü осевая сила, действующая на колесо -  ;
;
ü радиальная сила, действующая на колесо -  ;
;
ü окружная сила, действующая на колесо -  ;
;
ü расстояние между торцами для наружных колец подшипников -  ;
;
ü линейные размеры -  ,
,  ;
;
ü параметры выбранного подшипника:
Подшипник 206 ГОСТ 8338-75
Размеры:  Грузоподъемность:
Грузоподъемность: 






Радиальные реакции опор
Расстояние между точками приложения радиальных реакций при установке радиально-упорных подшипников по схеме «враспор»:
 ,
,

|
|
|
где  - смещение точки приложения радиальной реакции от торца подшипника, для шариковых радиальных однорядных подшипников:
- смещение точки приложения радиальной реакции от торца подшипника, для шариковых радиальных однорядных подшипников:
 ,
,

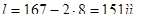 .
.
От сил в зацеплении
Ø  в плоскости YOZ:
в плоскости YOZ:
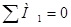 ;
;  ;
;

 ;
; 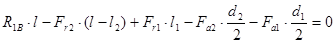 ;
;
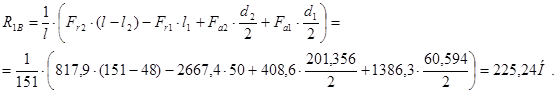
Проверка:  - реакции найдены правильно.
- реакции найдены правильно.
Ø в плоскости XOZ:
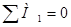 ;
;  ;
;
 .
.
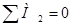 ;
;  ;
;

Проверка:  - реакции найдены правильно.
- реакции найдены правильно.
Суммарные реакции опор:
 ;
;
 .
.
Для расчета подшипников
 ;
;
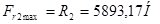 .
.
Внешняя осевая сила, действующая на вал:  .
.
Эквивалентные нагрузки
Для типового режима нагружения II коэффициент эквивалентности  .
.
 ;
;
 ;
;
 .
.
Эквивалентная динамическая радиальная нагрузка
Для радиальных шарикоподшипников из условия равновесия вала следует:  ,
, 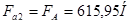 . Дальнейшие расчеты выполняем для более нагруженного подшипника опоры 2.
. Дальнейшие расчеты выполняем для более нагруженного подшипника опоры 2.
Отношение  ,
,
где  .
.
В соответствии с табл.7.3 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов) имеем:  .
.
Коэффициент осевого нагружения согласно табл.7.2 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов):
 .
.
Отношение 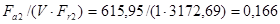 , что меньше
, что меньше  (
( при вращении внутреннего кольца). Окончательно принимаем согласно табл.7.2 [Глава 7] (уч..Ф. Дунаев, О.П. Леликов):
при вращении внутреннего кольца). Окончательно принимаем согласно табл.7.2 [Глава 7] (уч..Ф. Дунаев, О.П. Леликов):  ,
,  .
.
Принимаем согласно табл.7.6 [Глава 7](уч. П.Ф. Дунаев, О.П. Леликов)  ;
; 
 .
.
Эквивалентная динамическая радиальная нагрузка:
 .
.
Расчетный ресурс подшипника
Расчетный скорректированный ресурс подшипника при  (вероятность безотказной работы 90%),
(вероятность безотказной работы 90%),  (обычные условия применения),
(обычные условия применения),  (шариковый подшипник):
(шариковый подшипник):

Расчет подшипников на тихоходном валу
Исходные данные:
ü частота вращения вала -  ;
;
ü делительный диаметр шестерни быстроходной ступени -  ;
;
ü осевая сила, действующая на колесо -  ;
;
ü радиальная сила, действующая на колесо - 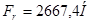 ;
;
ü окружная сила, действующая на колесо -  ;
;
ü расстояние между торцами для наружных колец подшипников -  ;
;
ü линейные размеры -  ,
,  ;
;
ü параметры выбранного подшипника:
Подшипник 212 ГОСТ 8338-75
|
|
|
Размеры:  Грузоподъемность:
Грузоподъемность: 






Радиальные реакции опор
 Расстояние между точками приложения радиальных реакций при установке радиально-упорных подшипников по схеме «враспор»:
Расстояние между точками приложения радиальных реакций при установке радиально-упорных подшипников по схеме «враспор»:
 ,
,
где  - смещение точки приложения радиальной реакции от торца подшипника, для шариковых радиальных однорядных подшипников:
- смещение точки приложения радиальной реакции от торца подшипника, для шариковых радиальных однорядных подшипников:
 ,
,

 .
.

От сил в зацеплении
Ø в плоскости YOZ:
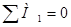 ;
;
 ;
;

 ;
;  ;
;

Проверка:  - реакции найдены правильно.
- реакции найдены правильно.
Ø в плоскости XOZ:
 ;
;  ;
;
 .
.
 ;
;  ;
;

Проверка:  - реакции найдены правильно.
- реакции найдены правильно.
Суммарные реакции опор:
 ;
;
 .
.
От действия муфты
Согласно ГОСТ Р 50891-96 значение радиальной консольной силы  для выходного вала редуктора:
для выходного вала редуктора:
 ,
,
где  - момент на входном валу.
- момент на входном валу.
 .
.
Реакции от силы  :
:

 ;
;  ;
;

 ;
;  ;
;
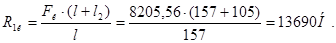
Проверка:  - реакции найдены правильно.
- реакции найдены правильно.
Для расчета подшипников
 ;
;
 .
.
Внешняя осевая сила, действующая на вал:  .
.
Эквивалентные нагрузки
Для типового режима нагружения II коэффициент эквивалентности  .
.
 ;
;
 ;
;
 .
.
|
|
|


