Эквивалентная схема биполярного и полевого транзисторов

Эквивалентную схему транзистора можно получить, если воспользоваться некоторыми методами теории электрических цепей, в частности, методами анализа линейных активных четырехполюсников. Четырехполюсником называется устройство, которое имеет две точки входа и две точки выхода. Биполярный и полевой транзисторы в любой схеме включения представляют собой четырехполюсник. Различают пассивные и активные четырехполюсники. Пассивные четырехполюсники не содержат источников напряжения или тока. Каскад усилителя на биполярном или полевом транзисторе способен усиливать мощность входного сигнала и является активным четырехполюсником. Теория четырехполюсников разработана для линейных систем, для которых характерна линейная зависимость между током и напряжением. Биполярный и полевой транзисторы являются нелинейными элементами. Однако, при работе в режиме малого сигнала, характерном для усилителей напряжения, усилитель на транзисторе можно считать линейным устройством, и применить к нему теорию линейных четырехполюсников.

На рис. 5.6 представлена эквивалентная схема линейного четырехполюсника. Каждый четырехполюсник характеризуется четырьмя величинами: током и напряжением на входе и током и напряжением на выходе.

Рис. 5.6. Эквивалентная схема четырехполюсника

В теории четырехполюсников зависимости между входными и выходными токами и напряжениями анализируют, используя режимы холостого хода и короткого замыкания на входе и выходе четырехполюсника. В результате параметры транзистора находятся из соответствующих уравнений для токов и напряжений. Поскольку к четырехполюсникам относятся различные по физическим принципам функционирования устройства, то уравнения для токов и напряжений будут в каждом случае разными. Существует шесть различных систем уравнений, описывающих связь токов и напряжений для разных видов четырехполюсников.

Будем рассматривать биполярный транзистор в схеме с общим эмиттером как активный линейный четырехполюсник.

 

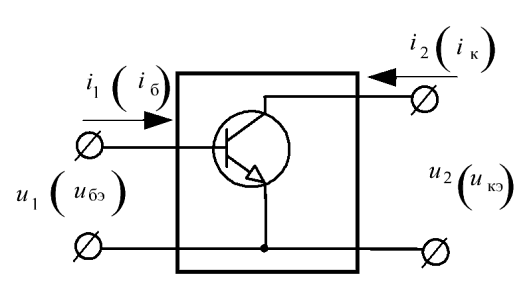
Рис. 5.7. Транзистор по схеме с общим эмиттером как четырехполюсник

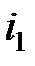Особенности биполярных транзисторов наилучшим образом учитываются системой уравнений в - параметрах. Для схемы с ОЭ в этой системе за независимые переменные берутся входной ток и выходное напряжение , а зависимыми будут входное напряжение и выходной ток . Таким образом, можно записать:

(5.12)

(5.13)

 

Для малых приращений переменных токов и напряжений запишем уравнения в полных дифференциалах:

(5.14)

 

(5.15)

Частные производные, вычисленные в окрестности рабочей точки транзистора, представляют собой некоторые постоянные величины – -параметры биполярного транзистора. Транзистор в малой окрестности рабочей точки (режим малых сигналов) может рассматриваться как линейный четырехполюсник относительно дифференциалов токов и напряжений. Благодаря линейности характеристик на малых участках изменения токов и напряжений дифференциалы в уравнениях можно заменить конечными приращениями. Для переменных составляющих токов и напряжений в активном режиме работы транзистора, когда токи и напряжения достаточно малы, можно перейти к системе уравнений в - параметрах:

 

, (5.16)

. (5.17)

Для транзистора по схеме с ОЭ уравнения можно записать в следующем виде:

, (5.18)

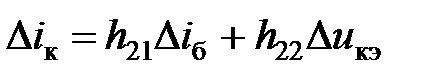. (5.19)

 

Биполярные транзисторы отличаются небольшим значением входного сопротивления и сравнительно высоким значением выходного сопротивления. Поэтому в такой схеме для нахождения -параметров уравнений легко осуществить режим короткого замыкания на выходе четырехполюсника и режим холостого хода на входе четырехполюсника.

Осуществляя режим холостого хода на входе четырехполюсника, найдем из уравнений 5.18 и 5.19 параметры и при и выясним их физический смысл:

- величина, обратная коэффициенту усиления по напряжению при разомкнутой входной цепи, характеризует внутреннюю обратную связь в биполярном транзисторе;

= - выходная проводимость транзистора при разомкнутой входной цепи.

Два оставшихся параметра можно найти, осуществив режим короткого замыкания на выходе четырехполюсника. При коротком замыкании на выходе 0. Тогда из уравнений 5.18 и 5.19 найдем:

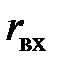
= - дифференциальное входное сопротивление транзистора при коротком замыкании на выходе;

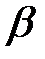= - коэффициент усиления тока базы транзистора при коротком замыкании на выходе.

Так как мы рассматриваем построение эквивалентной схемы биполярного транзистора для переменных составляющих токов и напряжений, то все токи и напряжения в уравнениях в -параметрах представляют собой переменные составляющие, соответствующие определенному режиму работы биполярного транзистора по постоянному току. Условие для переменной составляющей тока базы 0 соответствует условию для постоянной составляющей, величина которой определяется напряжением смещения. Условие для переменного напряжения =0 соответствует условию 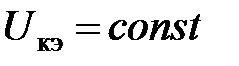для постоянного напряжения на коллекторе. При этих условиях -параметры принимают вид:

, (5.20)

, (5.21)

, (5.22)

. (5.23)

Параметр имеет размерность сопротивления и для его определения необходимо иметь семейство входных характеристик транзистора.

Параметр 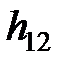также может быть найден по входной характеристике. Он является безразмерным, его величина мала и составляет, примерно, .

Параметр также является безразмерной величиной и его можно определить по семейству выходных характеристик.

Параметр имеет размерность проводимости и может быть определен из семейства выходных характеристик. Величина обратная называется выходным сопротивлением транзистора.

Определение -параметров позволяет получить физически обоснованную эквивалентную схему биполярного транзистора, широко используемую для анализа устройств на основе биполярного транзистора – усилителей, генераторов, преобразователей частоты. Первое уравнение (5.18) системы уравнений позволяет описать входную часть эквивалентной схемы, где последовательно включены входное сопротивление и эквивалентный генератор внутренней обратной связи. Второе уравнение (5.19) позволяет описать выходную часть эквивалентной схемы. Согласно второму уравнению изменение тока на выходе транзистора зависит от двух составляющих: управляемого генератора тока и величины , определяемой выходной проводимостью. Поэтому в выходную цепь эквивалентной схемы транзистора надо включить управляемый генератор тока и выходную проводимость. Эквивалентная схема биполярного транзистора, составленная на основе уравнений 5.18 и 5.19, при замене приращений переменных составляющих токов и напряжений конечными значениями

токов и напряжений, представлена на рис.5.8.

 

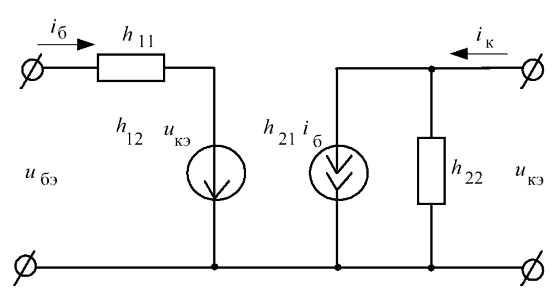
Рис.5.8. Эквивалентная схема биполярного транзистора

 

Проводя аналогичные рассуждения, можно получить эквивалентную схему полевого транзистора, представляя полевой транзистор, включенный по схеме с общим истоком, в виде линейного активного четырехполюсника, как показано на рис. 5.9.

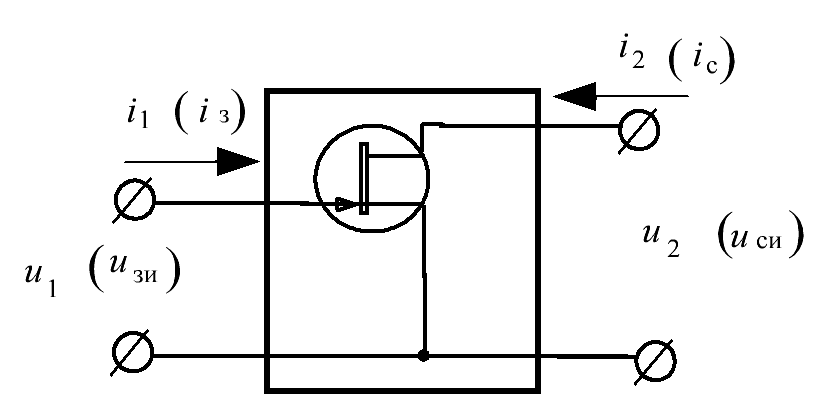
Рис. 5.9. Полевой транзистор как линейный четырехполюсник

Особенности полевых транзисторов наилучшим образом учитываются системой уравнений в - параметрах. Для схемы с ОИ в этой системе за независимые переменные берутся входное напряжение и выходное напряжение 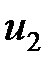, а зависимыми переменными будут входной ток и выходной ток 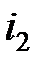. Эти зависимости можно представить следующими уравнениями:

, (5.24)

. (5.25)

 

Для малых приращений переменных токов и напряжений запишем уравнения в полных дифференциалах:

, (5.26)

 

. (5.27)

Частные производные, вычисленные в окрестности рабочей точки, представляют собой некоторые постоянные величины – -параметры полевого транзистора. Полевой транзистор в малой окрестности рабочей точки может рассматриваться как линейный четырехполюсник относительно дифференциалов токов и напряжений. Благодаря линейности характеристик на малых участках изменения токов и напряжений дифференциалы в уравнениях можно заменить конечными приращениями. Для переменных составляющих токов и напряжений в активном режиме работы транзистора, когда токи и напряжения достаточно малы, можно перейти к системе уравнений в - параметрах:

, (5.28)

. (5.29)

Полевые транзисторы отличаются высокими значениями величин входного и выходного сопротивлений. Поэтому для нахождения -параметров необходимо осуществить режим короткого замыкания на входе и на выходе четырехполюсника.

При коротком замыкании на входе 0, а при коротком замыкании на выходе =0. При этом из уравнений (5.28), (5.29) можно найти -параметры:

, , , .

Условие 0 означает, что равна нулю лишь переменная составляющая входного напряжения, а постоянная составляющая соответствует уровню начального смещения. Условие 0 означает, что равна нулю переменная составляющая выходного напряжения, а постоянная составляющая равна напряжению на стоке транзистора.

Для схемы с ОИ уравнения можно записать в следующем виде:

, (5.30) 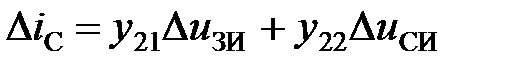. (5.31)

Из этих уравнений можно выяснить физический смысл - параметров:

- входная проводимость. Величина обратная входной проводимости равна входному сопротивлению полевого транзистора;

- коэффициент внутренней обратной связи междувыходной и входной цепями полевого транзистора. Его величина составляет, примерно, ;

- крутизна 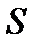полевого транзистора;

- выходная проводимость. Величина обратная выходной проводимости равна внутреннему сопротивлению полевого транзистора .

Крутизну и внутреннее сопротивление полевого транзистора можно найти из семейства выходных характеристик. Заменяя в системе уравнений приращения переменных составляющих токов и напряжений конечными значениями токов и напряжений, можно записать уравнения в следующем виде:

, (5.32)

. (5.33)

Определение -параметров позволяет получить физически обоснованную эквивалентную схему полевого транзистора, показанную на рис.5.10. Первое уравнение (5.32) позволяет описать входную часть эквивалентной схемы, где параллельно включены входная проводимость и эквивалентный генератор тока = , отражающий внутреннюю обратную связь в полевом транзисторе. Второе уравнение (5.33) позволяет описать выходную часть эквивалентной схемы, включающую в себя выходную проводимость и эквивалентный генератор тока , характеризующий усилительные свойства полевого транзистора.

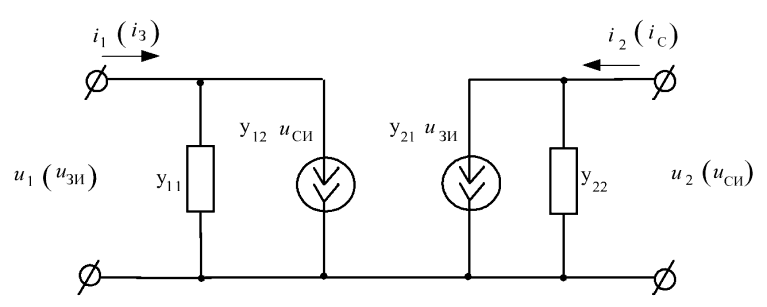
Рис.5.10. Эквивалентная схема полевого транзистора

Поскольку коэффициенты внутренней обратной связи достаточно малы, в дальнейшем анализе будем пренебрегать их величиной. С учетом этого можно исключить эти генераторы из левых частей эквивалентных схем и предложить единую упрощенную эквивалентную схему для биполярного и полевого транзисторов, представленную на рис. 5.11.

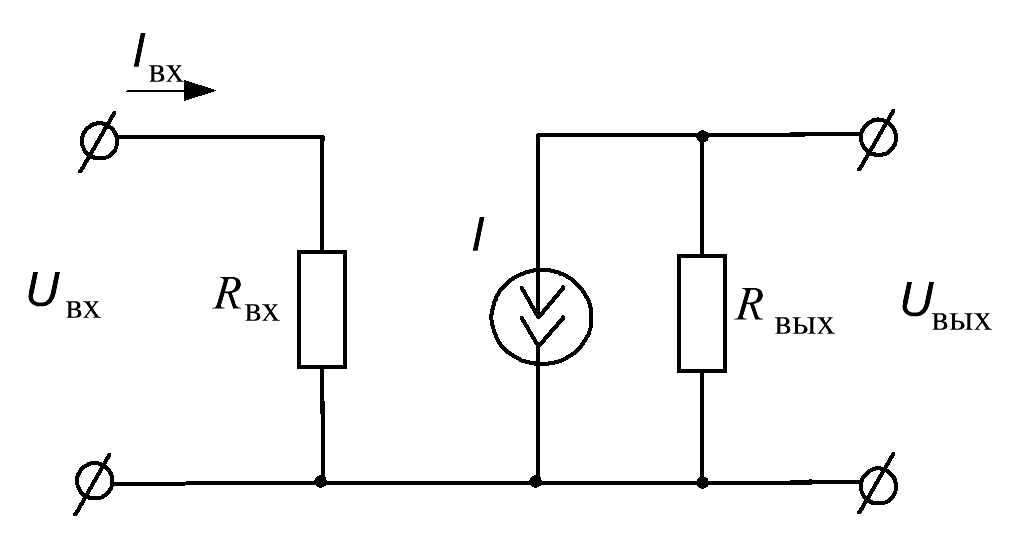
Рис. 5.11. Эквивалентная схема биполярного и полевого транзисторов

18

Область средних частот

Будем считать, что на вход каскада поступает напряжение от генератора гармонических сигналов. В области средних частот можно пренебречь влиянием обеих емкостей, входящих в эквивалентную схему усилителя на рис. 5.15. С учетом этого эквивалентная схема упростится и примет вид, показанный на рис. 5.16.

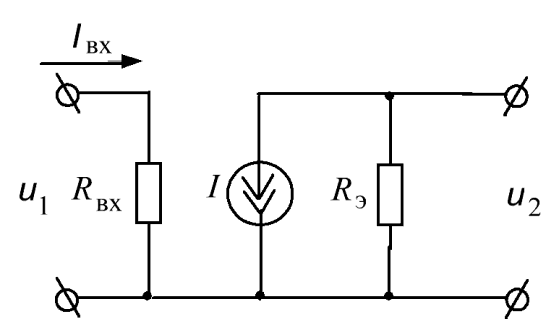
Рис. 5.16. Эквивалентная схема 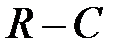- каскада в области средних частот

На этой схеме равно параллельному соединению резисторов 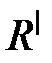и :

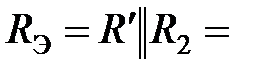
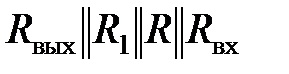. (5.34)

Коэффициент усиления каскада в области средних частот равен:

. (5.35)

Поскольку схемы с общим эмиттером и общим истоком инвертируют фазу входного сигнала, напряжение на выходе усилителя будет со знаком минус.

Для каскада на биполярном транзисторе ток на выходе , а входной ток . С учетом этого коэффициент усиления транзисторного каскада в области средних частот будет равен:

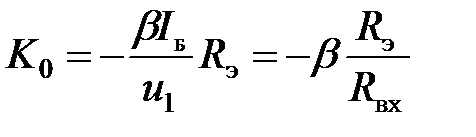. (5.36)

Если усиленное напряжение с выхода первого каскада усиления подается на вход такого же - каскада, то величина будет определяться низким значением входного сопротивления следующего каскада. В этом случае и коэффициент усиления каскада на биполярном транзисторе в области средних частот будет равен

Для каскада на полевом транзисторе ток на выходе равен: . Поэтому коэффициент усиления в области средних частот будет равен:

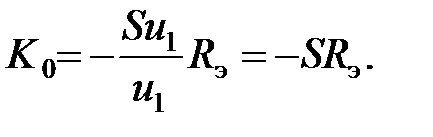(5.37)

Величина сопротивления определяется параллельным соединением четырех резисторов. Сопротивление стоковой нагрузки первого каскада усиления на эквивалентной схеме представлено резистором . Для усилителя на полевом транзисторе , , .

Поэтому для каскада на полевом транзисторе 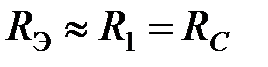и коэффициент усиления в области средних частот равен:

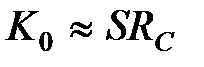. (5.38)

Область высоких частот

Выясним характер и поведение амплитудно-частотной характеристики каскада в области высоких частот. В области высоких частот также можно пренебречь влиянием емкости , так как на высоких частотах сопротивление ее мало и не влияет на величину коэффициента усиления. Пренебречь же влиянием емкости на высоких частотах нельзя. Поэтому эквивалентная схема в области высоких частот будет иметь следующий вид:

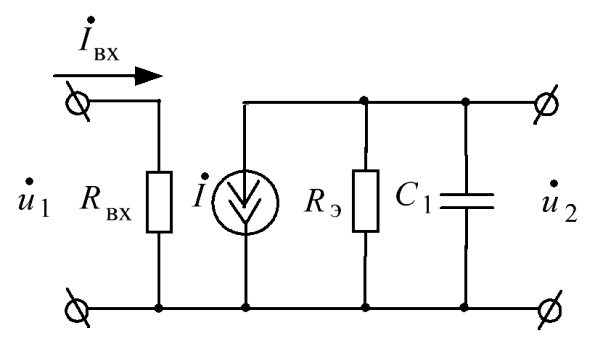
Рис. 5.17. Эквивалентная схема каскада в области высоких частот

Напряжение на выходе будет равно:

. (5.39)

Коэффициент усиления в области высоких частот равен:

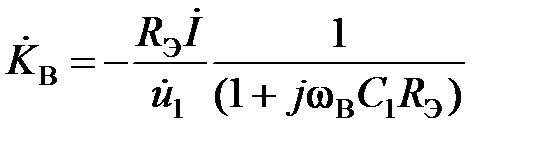(5.40)

Учитывая, что первый сомножитель этого выражения равен коэффициенту усиления в области средних частот, и обозначая , где - постоянная времени усилителя в области высоких частот, получим:

. (5.41)

Амплитудно-частотная характеристика каскада в области высоких частот описывается модулем коэффициента усиления:

. (5.42)

Фазовая характеристика каскада в области высоких частот:

(5.43)

Поведение АЧХ в области высоких частот определяется величиной постоянной времени нагрузочной цепи . Чем больше постоянная времени в области высоких частот, тем меньше коэффициент усиления в области высоких частот. Для каскада на биполярном транзисторе величину составляют сопротивление коллекторной нагрузки с параллельно включенным входным сопротивлением второго каскада и суммарная паразитная емкость. Поэтому эту постоянную времени называют постоянная времени нагрузочной цепи.

Для каскада на полевом транзисторе величину составляют сопротивление нагрузки в цепи стока первого каскада и суммарная паразитная емкость. Из эквивалентной схемы для области высоких частот видно, что параллельное соединение и представляет собой интегрирующую цепь, которая и определяет характер АЧХ в области высоких частот, показанной на рис. 5.18.

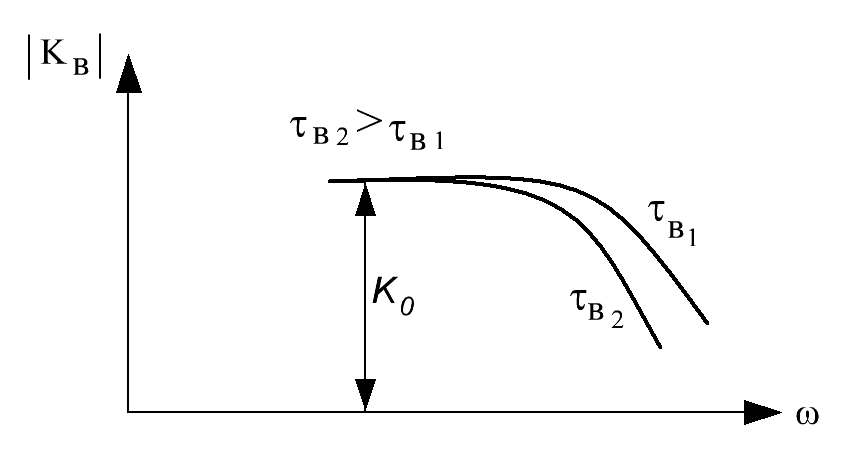
Рис. 5.18. Амплитудно-частотная характеристика 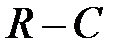- каскада в области высоких частот

Область низких частот

В области низких частот можно пренебречь влиянием емкости при этом эквивалентная схема принимает вид, показанный на рис. 5.19:

Рис. 5.19. Эквивалентная схема - каскада в области низких частот.

Напряжение на выходе этой схемы равно:

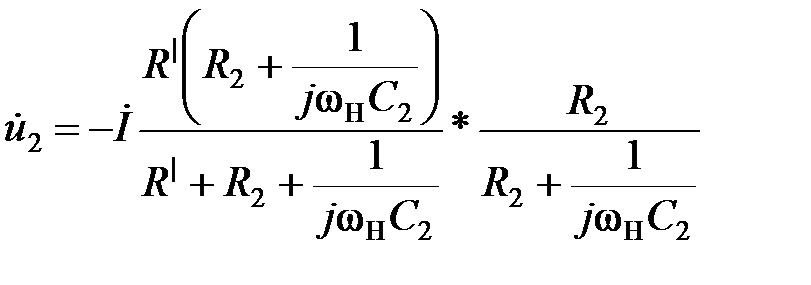. (5.44)

Сокращая числитель и знаменатель на и вынося в знаменателе за скобки (), получаем:

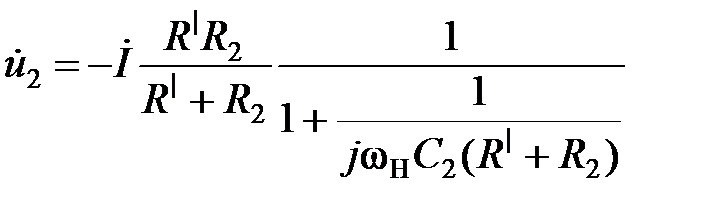= , (5.45)

где - постоянная времени в области низких частот. Коэффициент усиления в области низких частот:

. (5.46)

Модуль коэффициента усиления описывает амплитудно-частотную характеристику резистивно-емкостного усилителя в области низких частот.

. (5.47)

Сдвиг по фазе выходного напряжения относительно входного напряжения дается фазовой характеристикой:

. (5.48)

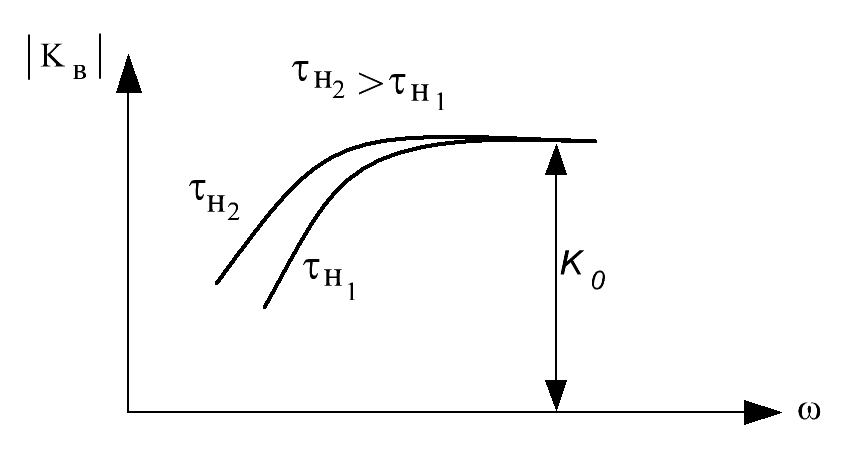
Рис. 5.20. Амплитудно-частотная характеристика каскада в области низких частот

Из рис. 5.20 видно, что поведение АЧХ зависит от постоянной времени в области низких частот. Чем больше постоянная времени, тем больше коэффициент усиления на низких частотах. Постоянная времени включает в себя разделительный конденсатор и резисторы 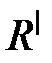и . Эту постоянную времени называют постоянной времени переходной цепи.

Переходная цепь представляет собой дифференцирующую цепь, которая определяет поведение АЧХ в области низких частот.

Зная поведение АЧХ каскада в области средних, низких и высоких частот, можно построить его АЧХ в широком диапазоне частот. Амплитудно-частотная характеристика резистивно-емкостного усилителя в относительном масштабе будет иметь вид, показанный на рис. 5.21.

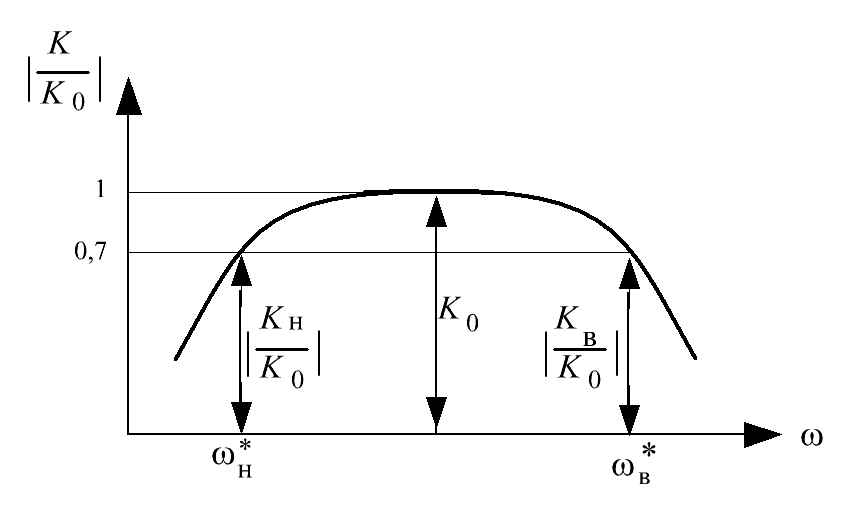
Рис. 5.21. Амплитудно-частотная характеристика - каскада

Ширина полосы пропускания 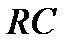каскада будет определяться значениями нижней и верхней граничных частот, на которых коэффициент усиления принимает значение 0,7 от максимального значения коэффициента усиления в области средних частот. Для границы полосы пропускания в области низких частот можно записать:

(5.49)

Из этого выражения нижняя граничная частота полосы пропускания равна:

(5.50)

Аналогично для границы полосы пропускания в области высоких частот:

. (5.51)

Из этого выражения верхняя граничная частота полосы пропускания усилителя равна:

. (5.52)

Таким образом, ширина полосы пропускания каскада определяется постоянными времени нагрузочной и переходной цепей этого каскада

 

19

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: