 |
Спектральный анализ периодических сигналов
|
|
|
|
В соответствии со спектральным способом анализа прохождения сигналов через линейные цепи любой случайный сигнал s (t) можно представить в виде бесконечной суммы элементарных аналитически однотипных детерминированных сигналов  :
:
 Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен
Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен 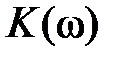 , элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.
, элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.
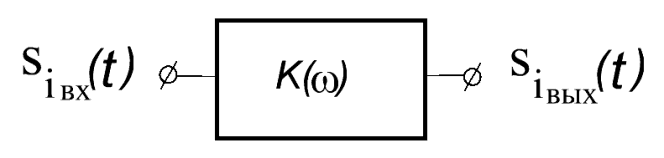
Рис.2.3. К определению сигнала на выходе линейной цепи.
Сигнал на выходе линейной цепи равен
 (2.9)
(2.9)
Поскольку для линейных цепей справедлив принцип суперпозиции, то результирующий отклик будет равен:
 (2.10)
(2.10)
Функции, описывающие элементарные сигналы, называются базисными функциями. Представление сигнала базисными функциями упрощается, если они являются ортогональными и ортонормированными.
Набор функций  называется ортогональным, если в интервале от
называется ортогональным, если в интервале от  до
до 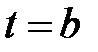
 при
при  (2.11)
(2.11)
и ортонормированным, если для всех  выполняется условие
выполняется условие
 . (2.12)
. (2.12)
Ортогональность базисных функций, с помощью которых представляется исходный сигнал  , является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от
, является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от 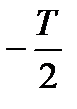 до
до  принимают лишь значения, равные
принимают лишь значения, равные  1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г.г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.
1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г.г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.
|
|
|
Рассмотрим вначале представление периодического электрического сигнала (рис. 2.4), отвечающего условию
 , (2.13)
, (2.13)
где:  - период сигнала;
- период сигнала;  =1,2,3,….
=1,2,3,….
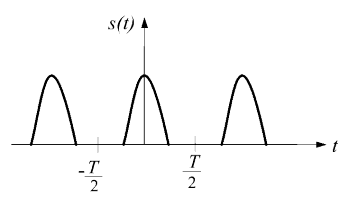
Рис. 2.4. Периодический сигнал
Представим этот сигнал бесконечным тригонометрическим рядом:
 . (2.14)
. (2.14)
Этот ряд называется рядом Фурье.
Возможна запись ряда Фурье в другом виде:
 , (2.15)
, (2.15)
где: 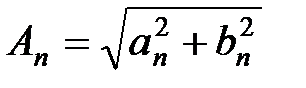 - модуль амплитуд гармоник;
- модуль амплитуд гармоник;
 - фазы гармоник;
- фазы гармоник;
 - круговая частота;
- круговая частота;
 - коэффициенты косинусоидальных составляющих;
- коэффициенты косинусоидальных составляющих;  - коэффициенты синусоидальных составляющих;
- коэффициенты синусоидальных составляющих;  - среднее значение сигнала за период (постоянная составляющая).
- среднее значение сигнала за период (постоянная составляющая).
Отдельные слагаемые рядов называют гармониками. Число  является номером гармоники.Совокупность величин
является номером гармоники.Совокупность величин  в ряде (2.15) называют спектром амплитуд, а совокупность величин
в ряде (2.15) называют спектром амплитуд, а совокупность величин  - спектром фаз.
- спектром фаз.
Ниже на рис. 2.5 представлены амплитудный и фазовый спектры периодического сигнала. Вертикальные отрезки амплитудного спектра представляют амплитуды гармоник и называются спектральными линиями.
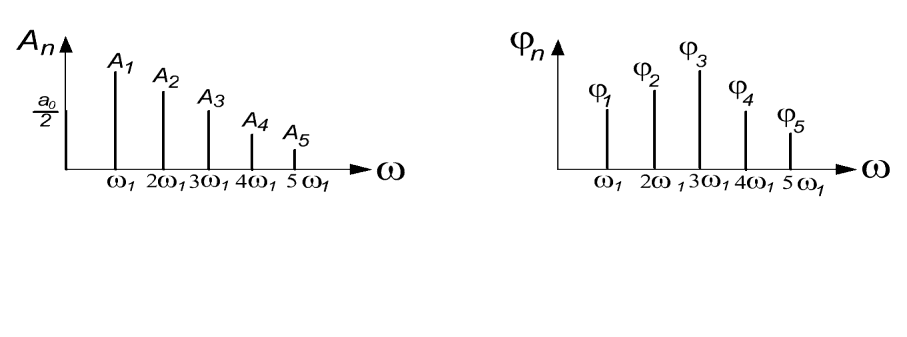
Рис 2.5. Амплитудный и фазовый спектры периодического сигнала
Таким образом, спектр периодического сигнала – линейчатый. Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый спектры.
Сумма ряда (2.15) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром. Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.
Если функция  , описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если
, описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если  - нечетная функция, то сумма будет содержать только синусоидальные составляющие.
- нечетная функция, то сумма будет содержать только синусоидальные составляющие.
|
|
|
Возможно также представление периодического сигнала в виде комплексного ряда Фурье:
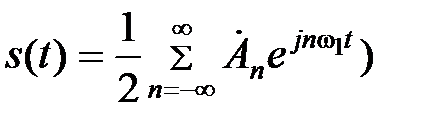 , (2.16)
, (2.16)
где:
 - комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.
- комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.
После подстановки значений  и
и  , получим:
, получим:
 (2.17)
(2.17)
Если подставить полученное значение  в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени
в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени  , либо комплексной амплитудой
, либо комплексной амплитудой  спектра.
спектра.
|
|
|


