 |
Элементы радиоэлектронных схем.
|
|
|
|
Радиоэлектронные цепи и устройства состоят из пассивных и активных элементов. Пассивными элементами являются резисторы, катушки индуктивности и конденсаторы. Сопротивление элементов электрической цепи току может быть двух видов – активное и реактивное. Если при прохождении тока по цепи происходят необратимые затраты электрической энергии, то сопротивление цепи называется активным. Если же подобной затраты нет, сопротивление называется реактивным. К активным сопротивлениям относятся резисторы, а к реактивным сопротивлениям – катушки индуктивности и конденсаторы. В действительности не существует чисто активных и реактивных сопротивлений. Такая терминология является следствием идеализации, так как любая катушка индуктивности обладает активным сопротивлением. Резистор же на высоких частотах обладает паразитной индуктивностью. Строго говоря, эти элементы нелинейные. Сопротивление, например, зависит от величины протекающего через него тока. Но во многих случаях отклонения от линейности незначительны, и мы вправе им пренебрегать.
Будем считать в последующем анализе резисторы, конденсаторы и катушки индуктивности линейными элементами. Ниже приводятся рисунки пассивных элементов и соответствующие линейные уравнения для токов и напряжений.
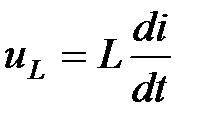
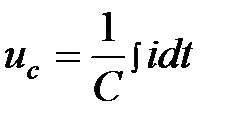
Рис.3.1. Пассивные элементы радиоэлектронных схем
К активным элементам относятся источники напряжений и источники токов, биполярные и полевые транзисторы, интегральные микросхемы, электронные лампы, клистроны, магнетроны, лазеры.
Наряду с пассивными и активными элементами в радиоэлектронике широко используются генераторы напряжения и генераторы тока.
Генератором напряжения называется источник напряжение, на выводах которого не зависит от сопротивления нагрузки и, следовательно, от тока нагрузки. Внутреннее сопротивление такого генератора равно
|
|
|
(3.1)
Генератором тока называется источник, ток которого не зависит от сопротивления нагрузки. Внутреннее сопротивление такого генератора равно бесконечности.
Реальные генераторы напряжения и тока отличаются от идеальных тем, что их выходные сигналы – напряжение и ток - зависят от сопротивления нагрузки. Это их свойство можно объяснить тем, что внутренние сопротивление генератора напряжения не равно нулю, а внутреннее сопротивление генератора тока не равно бесконечности. У реального генератора напряжения внутреннее сопротивление должно быть мало по сравнению с сопротивлением нагрузки. У реального генератора тока внутреннее сопротивление должно быть намного больше сопротивления нагрузки.
Линейные цепи – цепи, в которых все элементы линейные, то есть параметры зависят от значений напряжения и тока. Если эти параметры не изменяются во времени, то цепи называются линейными с постоянными параметрами.
такие цепи удовлетворяют принципу суперпозиции, согласно которому реакция линейной цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым воздействием в отдельности. Иными словами, если приложенное напряжение можно представить в виде суммы 
слагаемых
, (1.3)
то возникающий в каком-либо элементе (или участке) цепи ток также будет представлять собой сумму слагаемых
. (1.4)
8
ДИФФЕРЕНЦИРУЮЩИЕ ЦЕПИ
Сложные радиоэлектронные устройства состоят из простых цепей. Рассмотрим цепь, состоящую из резистора и конденсатора, включенных последовательно с идеальным генератором напряжения, показанную на рис. 3.3.
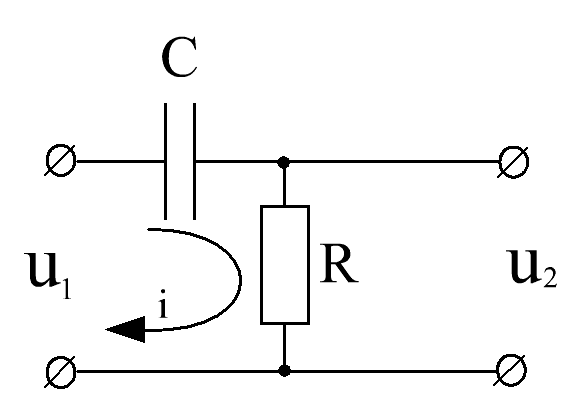
Рис.3.3. Дифференцирующая цепь
|
|
|
Если выходное напряжение снимается с резистора, то цепь называется дифференцирующей, если с конденсатора – интегрирующей. Эти линейные цепи характеризуются стационарными и переходными характеристиками. Это связано с тем, что изменение величины действующего в цепи напряжения приводит к тому, что токи и напряжения в различных участках цепи приобретают новые значения. Изменение состояния цепи происходит не мгновенно, а в течение некоторого интервала времени. Поэтому различают установившееся и переходное состояние электрической цепи.
Электрические процессы считаются установившимися (стационарными), если закон изменения всех напряжений и токов совпадает с точностью до постоянных величин с законом изменения действующего в цепи напряжения от внешнего источника. В противном случае считают, что цепь находится в переходном (нестационарном) состоянии.
К стационарным характеристикам относятся амплитудно-частотная и фазовая характеристики линейной цепи.
Нестационарное состояние линейной цепи описывается переходной характеристикой.
Будем считать, что к входу цепи подключен идеальный генератор напряжения 
. На основании второго закона Кирхгофа для дифференцирующей цепи можно записать дифференциальное уравнение, связывающее напряжения и ток в ветвях цепи:
(3.2)
Так как напряжение на выходе цепи 
, то:
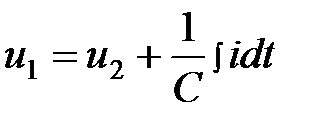(3.3)
Подставляя в интеграл значение тока, получим:
(3.4)
Продифференцируем левую и правую части последнего уравнения по времени:
(3.5)
Перепишем это уравнение, в следующем виде:
, (3.6)
где 
= 
- параметр цепи называемый постоянной времени цепи.
В зависимости от величины постоянной времени возможны два различных соотношения между первым и вторым слагаемыми правой части уравнения.
Если постоянная времени большая по сравнению с периодом гармонических сигналов 
>> 
или с длительностью импульсов 
>> 
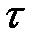, которые можно подавать на вход этой цепи, то
(3.7)
и напряжение на выходе цепи с небольшими искажениями повторяет входное напряжение:
. (3.8)
Если же постоянная времени мала по сравнению с периодом гармонических сигналов 
<< или с длительностью импульсов 
<< 
, то
. (3.9)
Отсюда напряжение на выходе равно:
|
|
|
. (3.10)
Таким образом, в зависимости от величины постоянной времени такая -цепь может либо с определенными искажениями передавать входной сигнал на выход, либо с определенной степенью точности его дифференцировать. При этом форма выходного сигнала будет разной. Ниже на рис. 3.4 представлены входное напряжение, напряжения на резисторе и конденсаторе для случаев, когда постоянная времени велика 
и постоянная времени мала 
.
аб
Рис. 3.4. Напряжения на элементах дифференцирующей цепи при 
(а) и 
(б)
Теперь определим коэффициент передачи дифференцирующей цепи. Комплексный коэффициент передачи дифференцирующей цепи при подаче на вход гармонического сигнала равен:
. (3.11)
Обозначим отношение 
, где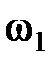 
- граничная частота полосы пропускания дифференцирующей цепи.
Выражение для коэффициента передачи примет вид:
. (3.12)
Модуль коэффициента передачи равен: 
. (3.13)
- граничная частота полосы пропускания, на которой модуль реактивного сопротивления становится равным величине активного сопротивления, а коэффициент передачи цепи равен 
. Зависимость модуля коэффициента передачи от частоты называется амплитудно–частотной характеристикой (АЧХ).
Зависимость угла сдвига фаз между выходным и входным напряжениями от частоты называется фазовой характеристикой (ФЧХ). Фазовая характеристика:
(2.14)
Ниже на рис. 3.5 представлены АЧХ и ФЧХ дифференцирующей цепи:
Рис. 3.5. Амплитудно–частотная и фазовая характеристики
дифференцирующей цепи
Из амплитудно-частотной характеристики видно, что прохождение сигналов через дифференцирующую цепь сопровождается уменьшением амплитуд низкочастотных составляющих его спектра. Дифференцирующая цепь является фильтром высоких частот.
Из фазовой характеристики видно, что фазы низкочастотных составляющих сдвигаются на больший угол, чем фазы высокочастотных составляющих.
Переходную характеристику дифференцирующей цепи можно получить, если на вход подать напряжение в виде единичного скачка.
|
|
|
Таким образом, аналитическое выражение для переходной характеристики дифференцирующей цепи записывается в следующем виде:
, (3.21)
На рисунках ниже приведено напряжение единичного скачка и переходная характеристика дифференцирующей цепи.
Рис. 3.6. Единичный скачок и переходная характеристика дифференцирующей цепи
При 
переходная характеристика 
.
Постоянная времени 
- это время, за которое напряжение на выходе дифференцирующей цепи изменяется до уровня 0,37 от начального уровня входного сигнала в виде единичного скачка.
Дифференцирующая цепь укорачивает входные импульсы. Однако дифференцирующие цепи чаще всего применяются не для дифференцирования, а для разделения переменной и постоянной составляющих напряжения. В этом случае постоянную времени цепи берут достаточно большой, чтобы избежать искажений сигнала за счет его дифференцирования.
ИНТЕГРИРУЮЩИЕ ЦЕПИ.
Рис. 3.7. Интегрирующая цепь
На основании второго закона Кирхгофа запишем дифференциальное уравнение для токов и напряжений в интегрирующей цепи:
. (3.22)
Учитывая, что напряжение на выходе
, (3.23)
найдем ток:
. (3.24)
Подставим значение тока в предыдущее уравнение:
(3.25)
В зависимости от величины постоянной времени 
возможны два различных соотношения между первым и вторым слагаемыми в правой части уравнения (3. 25). Если постоянная времени мала по сравнению с периодом гармонических сигналов 
<< 
или с длительностью импульсов 
<< , которые можно подавать на вход этой цепи, то
. (3.26)
В этом случае
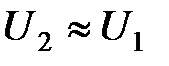. (3.27)
Если же постоянная времени большая по сравнению с периодом гармонических сигналов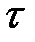 
>> или с длительностью импульсов 
>> , которые можно подавать на вход этой цепи то
. (3.28)
Отсюда
(3.29)
Таким образом, в зависимости от соотношения величины постоянной времени и параметров входных сигналов эта цепь может либо с определенными искажениями передавать входной сигнал на выход, либо с некоторой погрешностью его интегрировать. На рис.3.8 приведены формы импульсов на выходе интегрирующей цепи для различных значений постоянной времени. При 
цепочка интегрирует входной сигнал, а при 
цепочка с искажениями передает сигнал на выход.
а б
Рис. 3.8. Напряжения на входе и элементах интегрирующей цепи при 
(а) и 
(б).
Считается, что когда 
цепочка интегрирует.
Определим параметры и характеристики интегрирующей цепи. Коэффициент передачи интегрирующей цепи равен:
(3.30)
Обозначим
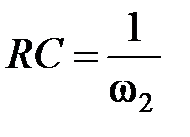
, (3.31)
где 
граничная частота полосы пропусканияинтегрирующей цепи.
Приравняв модуль коэффициента передачи
, (3.32)
найдем граничную частоту
|
|
|
. (3.33)
Модуль коэффициента передачи запишем в следующем виде
(3.34)
Амплитудно-частотная характеристика интегрирующей цепи представляет собой зависимость модуля коэффициента передачи от частоты.
Найдем фазо-частотную (фазовую) характеристику интегрирующей цепи:
(3.35)
На рис. 2.9 приведены амплитудно-частотная и фазовая характеристики интегрирующей цепи.
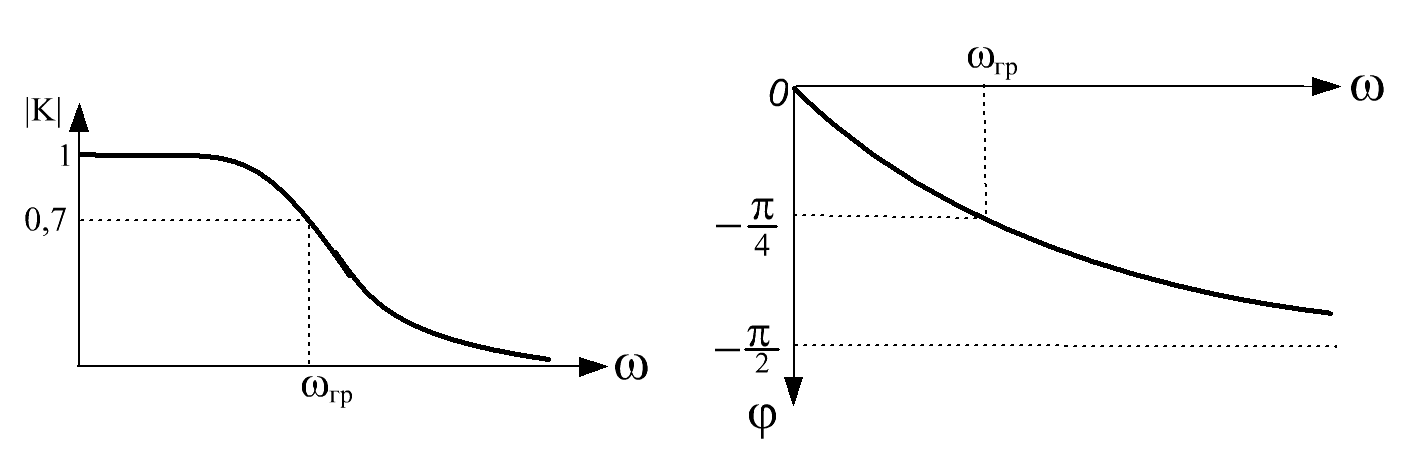
Рис. 3.9. Амплитудно-частотная и фазовая характеристики интегрирующей цепи
Интегрирующая цепь является фильтром низких частот. При прохождении сигналов через интегрирующую цепь удельный вес высокочастотных составляющих спектра сигнала уменьшается, а фазы этих составляющих сдвигаются на больший угол, чем фазы низкочастотных составляющих.
Таким образом, переходная характеристика интегрирующей цепи
. (3.44)
При 
Отсюда следует физический смысл постоянной времени интегрирующей цепи:
- это время, за которое напряжение на выходе интегрирующей цепи изменяется до уровня 0,63 от начального уровня входного напряжения.
Единичный скачок и переходная характеристика интегрирующей цепи представлены на рис. 3.10.
Рис.3.10. Единичный скачок и переходная характеристика интегрирующей цепи
9 РЕЗОНАНСНЫЕ (КОЛЕБАТЕЛЬНЫЕ) КОНТУРЫ
Колебательный контур – это линейная электрическая цепь, составленная из конденсатора 
и катушки индуктивности 
С их помощью решается одна из важнейших задач радиотехники – осуществление частотной селекции (избирательности). Из множества несущих частот различных радиостанций, поступающих в антенну радиоприемника, необходимо выбрать узкую полосу частот интересующей нас радиостанции.
|
|
|
