Главная | Обратная связь | Поможем написать вашу работу!

Резонанс токов в параллельном колебательном контуре

Параллельный колебательный контур состоит из параллельно включенных катушки индуктивности и конденсатора, как показано на рис. 3.17. Активное сопротивление катушки индуктивности равно , а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению . Контур питается идеальным генератором тока.

Рис. 3.17. Параллельный колебательный контур.

Входное сопротивление контура равно:

. (3.92)

Для высокодобротных контуров в области резонансной частоты и . Учитывая это, можно записать:

(3.93)

где: ; .

Таким образом, входное сопротивление зависит от частоты. Токи в ветвях контура также зависят от частоты. На резонансной частоте сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток

. (3.94)

Входное сопротивление контура при резонансе становится активным и равно:

(3.95)

Следовательно, ток в контуре на резонансной частоте равен:

(3.96)

Таким образом, токи в ветвях контура при резонансе в раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.

Зависимость отношения амплитуды напряжения на контуре на текущей частоте к амплитуде напряжения на контуре на резонансной частоте от частоты называют АЧХ параллельного контура.

Запишем выражение для амплитудно-частотной характеристики параллельного контура:

(3.97)

. (3.101)

Таким образом, АЧХ параллельного и последовательного контуров описываются одним и тем же выражением.

Фазовая характеристика параллельного контура (рис. 2.18) построена на основании выражения

(3.102)

Рис. 3.18. Фазовая характеристика параллельного контура

10 Связанные контуры

Недостатком одиночных колебательных контуров является их плохая избирательность. Количественно избирательность оценивается коэффициентом прямоугольности, который равен отношению ширины полосы пропускания на уровне 0,7 к ширине полосы пропускания на уровне 0,1 (иногда на уровне 0,01):

. (3.107)

Чем ближе значение коэффициента прямоугольности к 1, тем лучше избирательность контура.

Коэффициент прямоугольности одиночного контура = 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21.

Ценным свойством связанных контуров является возможность осуществить АЧХ по форме, близкую к прямоугольной. Связанные контуры взаимно влияют друг на друга. Степень влияния зависит от сопротивления связи. В качестве элементов связи используют конденсаторы и индуктивности. Чаще всего используют индуктивную (трансформаторную) связь. В этом случае степень связиопределяется коэффициентом взаимной индукции . В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где - коэффициент взаимной индукции, – сопротивление связи.

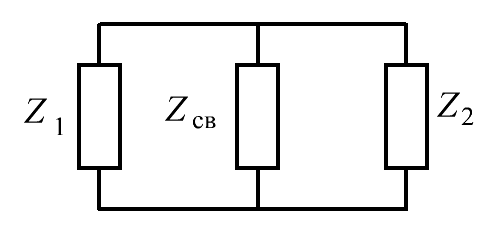
Рис. 3.20. Связанные контуры и их эквивалентная схема

Коэффициент взаимной индукции равен:

, (3.108)

где: - магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;

- магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.

Для неферромагнитной среды .

Эдс, индуцируемая во втором контуре, равна:

(3.109)

Сопротивление связи равно

. (3.110)

Степень связи между контурами оценивается коэффициентом связи , который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.

Коэффициент передачи напряжения из первого контура во второй равен:

(3.111)

Если включить генератор во второй контур, то получим коэффициент передачи напряжения из второго контура в первый:

. (3.112)

Коэффициент связи между контурами равен среднему геометрическому из коэффициентов передачи:

(3.113)

Коэффициент связи выражает отношение общего магнитного потока, пронизывающего обе катушки индуктивности, к полному магнитному потоку. Величина () характеризует поток рассеяния.

Выясним характер и форму амплитудно-частотной характеристики системы из двух индуктивно связанных контуров, представленных на рис.2.20.Для упрощения предположим, что контурысостоят из одинаковых элементов и поэтому имеют одинаковую резонансную частоту . АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте . Две другие соответствуют максимуму коэффициента передачи и будут на частотах

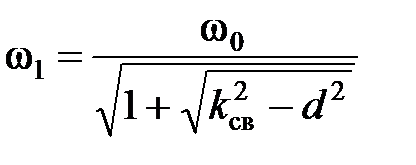, (3.114)

. (3.115).

Частоты зависят от коэффициента связи и величины затухания контуров и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи. - быстрая частота связи, а - медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.