 |
Интегрирование рациональных дробей.
|
|
|
|
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
КУРС ЛЕКЦИЙ
По дисциплине «Математика» 2 семестр
Для студентов заочной формы обучения
Раздел № 2 «Неопределенный и определенный интегралы.
Приложение определенного интеграла»
Волгодонск
Первообразная и неопределенный интеграл.
Определение: Первообразной F(x) для функции f(x) на промежутке 
называют функцию, производная которой 
.
Пример. Для функции 
: первообразная 
на R, так к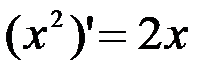 
при любом х.
Лемма. Если производная функции на промежутке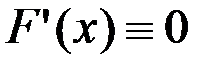 
, то 
.
Доказательство: По теореме Лагранжа для любых x1, x2 Î выполняется 
, где 
, так как 
Þ 
Þ 
Þв силу произвольности точек x1 и x2 F(x) = C(const).
Ч.т.д.
Теорема: Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x) Þ F(x)=Ф(x)+С.
Доказательство: так как 
Þ по Лемме 
Þ 
.
Ч.т.д.
Таким образом, из теоремы следует, что выражение 
описывает все множество первообразных функции f(x).
Определение: Неопределенным интегралом функции f(x) по переменной x называется множество всех её первообразных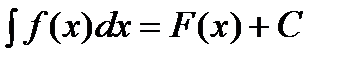 
, где 
.
ò ‒ знак интеграла, f(x) – подынтегральная функция, x – переменная интеграла, 
‒ подынтегральное выражение, С – const интегрированная.
Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат.
; 
- верно.
Свойства неопределенного интеграла.
| |
| |
| |
| |
| |
| |
|
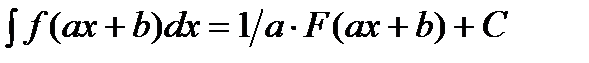
Замена переменных в неопределенном интеграле.
Пусть функция является дифференцируемой и обратимой 
, на множестве значений которой определена функция 
Þ 
= 
.
|
|
|
Пример: 
= 
= 
= 
= 
= 
= 
.
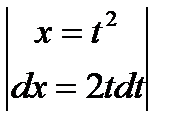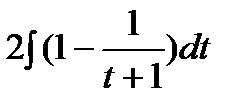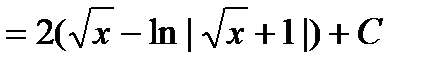Пример: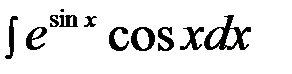 
= 
= 
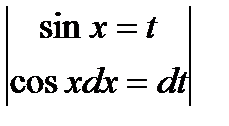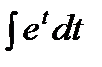=et+C=esin x+C.
Таблица интегралов.
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
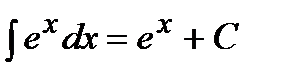
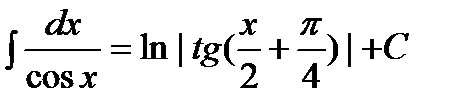
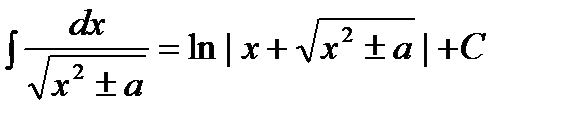
Интегрирование по частям в неопределенном интеграле.
Т.к. 
Þ 
. Проинтегрируем обе части равенства:
.
Интегрирование по частям применяют, когда сложный интеграл можно заменить интегрированием более простого. Рассмотрим применение метода в следующих случаях:
1. Подынтегральная функция представляет собой произведение многочлена на показательную функцию или тригонометрическую. За u берется многочлен, за dv – оставшуюся часть подынтегрального выражения.
Пример1:
= 
=
= 
= 
.
Пример2:
= 
= 
=
= 
= 
.
2. Подынтегральная функция представляет собой произведение многочлена на логарифмическую или обратную тригонометрическую функцию. За часть u нужно взять логарифмическую или обратную тригонометрическую функцию.
Пример3:
= 
= 
= 
= 
= 
.
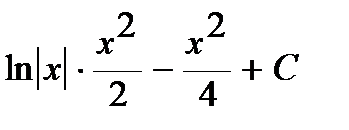Пример4:
= 
= 
= 
.
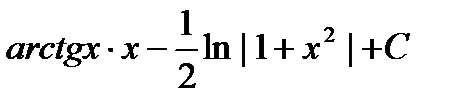3. Подынтегральная функция представляет собой произведение тригонометрической на показательную функцию. Не важно что брать за u.
Пример5:
I= 
= 
= 
= 
= 
.
Последний интеграл есть не что иное как исходный интеграл, поэтому можно
записать:
; 
; 
.
4. Иногда метод интегрирования по частям приходится применять несколько раз.
Пример 6:
=
= 
= 
=
= 
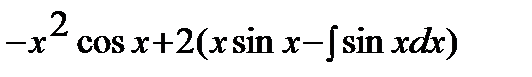5. Если неверно выбраны u и dv, то в результате интегрирования получим более сложное выражение под интегралом, чем в исходном.
Пример 7:
= 
+ 
…,
отсюда видно, что полученный интеграл сложнее исходного.
Интегрирование выражений, содержащих квадратный трехчлен.
; 
.
Каждый из указанных двух интегралов берется в два приема:
а) выделяется полный квадрат в квадратном трехчлене:
;
б) заменой 
исходный интеграл сводится к табличным интегралам.
Пример8: Найти неопределенный интеграл.
|
|
|
.
Решение:
Выделим сначала полный квадрат из квадратного трехчлена: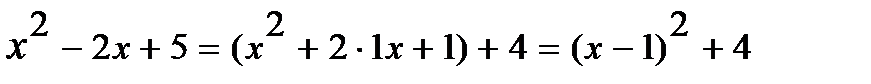 
.
Затем проведем замену переменных, положив 
и 
.
Тогда
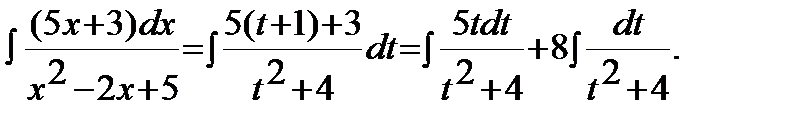
Каждый из интегралов вычислим отдельно:
.
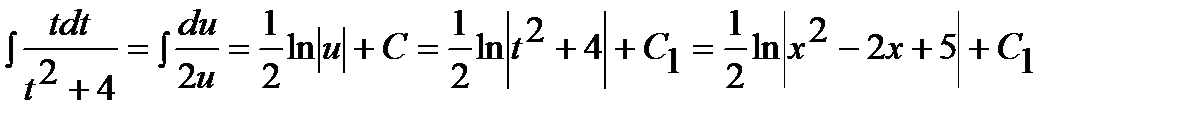Здесь мы сделаем замену переменных, положив 
(тогда 
и 
):
= 
Окончательно получим
Пример 9: Найти неопределенный интеграл.
Интегрирование рациональных дробей.
Выражения вида 
, где а - вещественное, k, l - натуральные числа, а квадратный трехчлен 
не имеет действительных корней, назовем простейшими сомножителями.
Известна основная теорема алгебры: любой многочлен 
степени n можно разложить в произведение простейших сомножителей:
= 
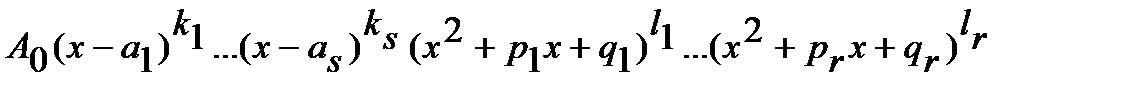(4)
где 
-число; 
Дроби вида 
, где k, l - натуральные числа,
- простейший сомножитель, будем называть простейшими рациональными дробями.
Определение. Дробь 
называется правильной, если 
(здесь
m и n степени многочленов, стоящих в числителе и в знаменателе, соответственно. Если m≥n, дробь называется неправильной.
Каждую неправильную дробь можно представить в виде суммы многочлена и правильной дроби: 
.
Можно доказать следующую теорему.
Теорема. Любая правильная рациональная дробь 
, где 
многочлен, определённый равенством (4), может быть представлена в виде суммы простейших рациональных дробей (m и n — степени многочленов, стоящих в числителе и знаменателе соответственно). Эта сумма строится следующим образом в два этапа:
1) каждый простейший множитель вида 
порождает следующую сумму из 
слагаемых: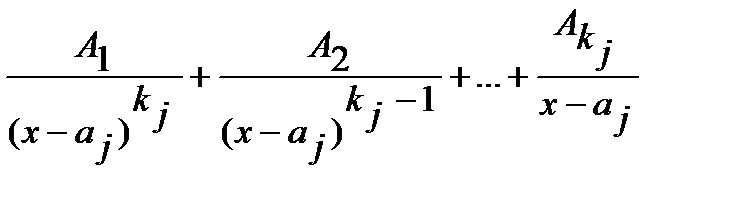 
;
2) каждый сомножитель вида 
порождает следующую сумму из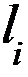 
слагаемых: 
В результате мы получим следующее разложение правильной дроби на простейшие: 
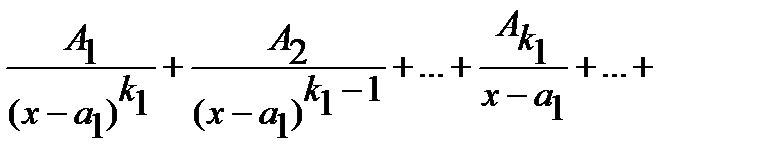
(5)
Считая в дальнейшем, что коэффициент при старшей степени у многочлена равен единице, на примерах решения задач покажем, как используется сформулированная теорема на практике.
Пример: Разложить дробь 
на простейшие дроби.
Решение: Разложим знаменатель на простейшие сомножители: 
.
Тогда 
; 
Две дроби, имеющие одинаковые знаменатели, равны, значит равны их числители, то есть 
.
Два многочлена тождественно равны тогда, когда у них совпадают коэффициенты при одинаковых степенях 
, следовательно, можно записать следующую систему уравнений:
.
Решая ее, находим, что 
|
|
|
Окончательно положим 
.
Пример: Разложить дробь 
на простейшие дроби. Решение: Разложим дробь на простейшие:
Тогда 
.
Как и в предыдущей задаче, составим систему уравнений для нахождения неизвестных коэффициентов:
Отсюда 
Следовательно, 
.
Из разложения (5) следует, что интегрирование правильных рациональных дробей сводится к интегрированию простейших дробей.
Пример: Найти 
.
Решение: Поскольку рациональная дробь, стоящая под знаком интеграла, является неправильной, то представим ее в виде суммы многочлена и правильной дроби (для этого достаточно найти частное и остаток от деления числителя на знаменатель).
Тогда 
.
Разложим дробь 
на простейшие дроби:
;
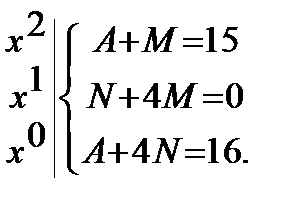
Отсюда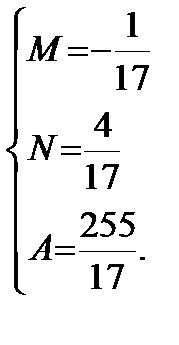 
Следовательно,
Но тогда:
= 
|
|
|
