 |
Несобственные интегралы первого рода (по бесконечному промежутку).
|
|
|
|
Определение: Пусть функция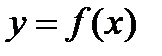 
непрерывна на промежутке 
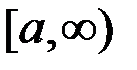, тогда очевидно, что при любом 
имеет смысл интеграл 
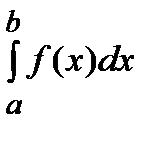. Будем расширять промежуток 
, увеличивая . Тогда, если существует предел:
, то этот предел называется несобственным интегралом от функции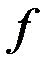 
по бесконечному промежутку 
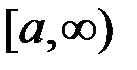и обозначается 
.
Отметим, что если указанный предел существует и конечен, то интеграл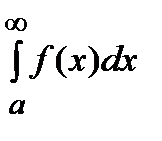 
называется сходящимся (говорят, что он сходится). В противном случае (если предел бесконечен или не существует) говорят, что 
расходится.
Аналогично вводится понятие несобственного интеграла 
по промежутку 
.
Определение: Несобственный интеграл 
определяется как следующая сумма несобственных интегралов:
= 
+ 
.
Отметим, что легко показать, что так определенный интеграл 
не зависит от выбора точки 
. Этот интеграл называется сходящимся, если сходящимися являются интегралы 
и 
, в противном случае он называется расходящимся.
Примеры:
1. Вычислить несобственный интеграл или доказать его расходимость:
а) 
= 
= 
= 
=
= 
= 
= 
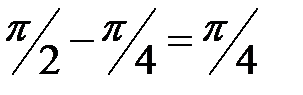
б) 
= 
= 
= 
= 
(интеграл расходится)
в) 
= 
= 
= 
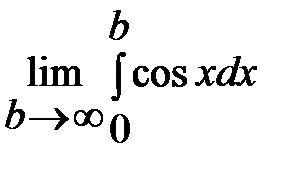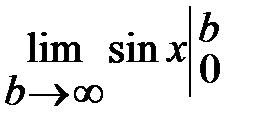Поскольку последний предел не существует, то интеграл расходится.
Несобственные интегралы второго рода (от неограниченных функций).
Предположим теперь, что функция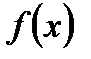 
непрерывна на , за исключением точки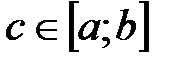 
, в которой она терпит разрыв второго рода, и рассмотрим три случая:
а) 
.
Возьмем произвольное, но достаточно малое (чтобы выполнялось неравенство 
) положительное 
и положим, по определению,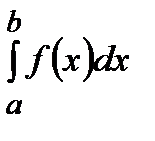 
= 
Если указанный предел существует, то 
называется несобственным интегралом второго рода по промежутку .
б) 
.
Как и в предыдущем случае определим несобственный интеграл 
, положив:
= 
.
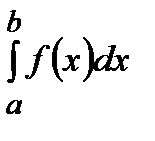Отметим, что вся терминология, связанная с определением сходимости и расходимости несобственных интегралов второго рода полностью переносится с соответствующих определений, данных для интегралов первого рода.
|
|
|
в)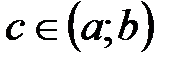 
В этом случае полагаем:
= 
+ 
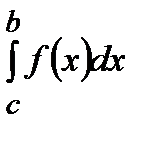
При этом будем считать, что последний несобственный интеграл сходится, если сходятся слагаемые, определяющие этот интеграл. Ясно, что,
= 
+ 
.
Пример.
= 
= 
= 
=
= 
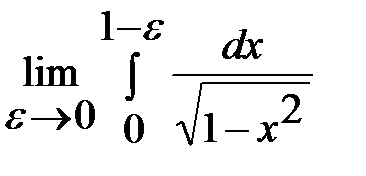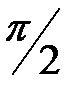
Признаки сходимости несобственных интегралов.
Теорема (признак сравнения).
Если на промежутке 
непрерывные функции 
и 
удовлетворяют условию 
для 
, то из сходимости интеграла 
следует сходимость интеграла 
, а из расходимости 
следует расходимость 
.
Доказательство. Предположим, что интеграл 
сходится и равен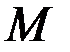 
, тогда для любого будет выполняться неравенство: 
и, следовательно, будут выполняться неравенства: 
. Если теперь на интеграл 
смотреть как на функцию от , то эта функция будет монотонно возрастающей на бесконечном промежутке 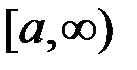и ограниченной на этом промежутке. Следовательно, она имеет конечный предел: 
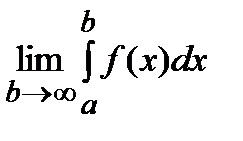, то есть интеграл 
сходится.
Если теперь интеграл 
расходится, то возрастающая функция 
стремится к 
при 
. Но тогда, тем более, будет стремиться к 
и функция 
, так как 
. То есть интеграл 
будет расходиться.
Теорема (предельный признак сравнения).
Если на промежутке 
функции 
и 
непрерывны и неотрицательны, а предел их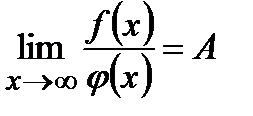 
, где 
- число, не равное нулю, то оба несобственных интеграла 
и 
либо сходятся, либо расходятся одновременно.
Мы не будем приводить доказательство этой теоремы, а укажем только направление рассуждений для организации доказательства.
Указание. Если выбрать 
настолько малым, чтобы окрестность 
не содержала 
, то для «больших» 
будет выполняться неравенство 
, или 
и остается воспользоваться первым признаком сравнения.
Теорема.
Если функция 
непрерывна на промежутке 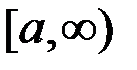и интеграл 
сходится, то сходится и интеграл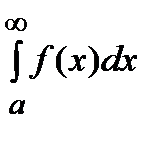 
.
|
|
|
Доказательство: Рассмотрим две функции:
и 
.
(заметим, что функция 
совпадает с функцией 
в тех точках, где последняя положительна, и равна нулю в остальных точках, а функция 
совпадает с функцией 
в тех точках, где она отрицательна, и равна нулю в остальных точках).
Очевидно, что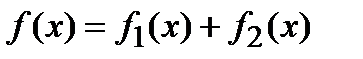 
. Воспользовавшись теоремой сравнения (в нашем случае 
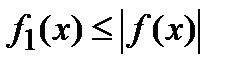и 
), можно утверждать, что интегралы 
и 
, а значит и 
сходятся. Но тогда будет сходиться и интеграл 
, поскольку для него справедливо равенство:
= 
+ 
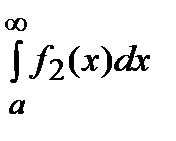
Проверка последнего равенства осуществляется заменой интегралов по бесконечному промежутку соответствующими пределами.
Отметим, что если вместе с интегралом 
сходится и интеграл 
, то интеграл 
называется абсолютно сходящимся, в противном случае (если сходится только интеграл 
) он называется условно сходящимся.
Аналогичные теоремы можно сформулировать как для несобственных интегралов первого рода по промежуткам и 
, так и для несобственных интегралов второго рода.
|
|
|
