 |
Полярная система координат.
|
|
|
|
Рассмотрим на плоскости точку О, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью.
Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа r - длина радиус-вектора 
и j - угол между радиус-вектором точки M и положительным направлением полярной оси.
Таким образом, любая точка в полярной системе координат будет иметь две координаты M(r,j), r – полярный радиус, j – полярный угол. Очевидно, что r – величина неотрицательная (как длина любого вектора), а угол может выбираться по договоренности (для однозначности определения координат) из промежутков 
или 
.
Если угол j откладывается от полярной оси против хода часовой стрелки, то его будем считать положительным, если по часовой стрелке, то отрицательным.
Изображение линий в полярной системе координат.
r= R – окружность с центром в полюсе и радиусом R.
j= a - луч под углом 
к полярной оси.
r= j – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла j и вычислять соответственно значения полярного радиуса r. Если r получится меньше нуля, то картинки не будет (этой части рисунка не будет)
| Спираль Архимеда | Кардиоида | 3-х лепестковая роза | Лемниската Бернулли | |
| r=j | r=1+cosj | r=cos3j | r=4cosj | r2=cos2j |
| 
| 
| 
| 
|
Связь между декартовой и полярной системами координат.
Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (r;j) к декартовым (x;y):
, и от декартовых к полярным: 
, 
Вычисление площади криволинейного сектора.
|
|
|
Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора.
Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами j=a и j=b и кривой, заданной в полярной системе координат r=r(j).
Разобьем криволинейный сектор лучами j=ji, i = 0…n на части
a=j0<j1<j2<…<jn=b
j =a, j =b, r =r(j).
| a |
| b |
| r=r(j) |
В каждой части произвольным образом выбираем точку Ci и вычисляем в ней значение ri =r(Ci) угол i - части 
. Заменим площадь i - части площадью кругового сектора 
= 
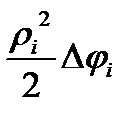
Просуммируем площади всех круговых секторов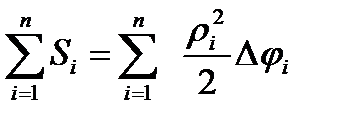 
.
Сумма этих площадей приближенно равна площади исходного криволинейного сектора. Причем, чем больше будет частей разбиения, тем меньше будет Dji, тем точнее будет равенство.
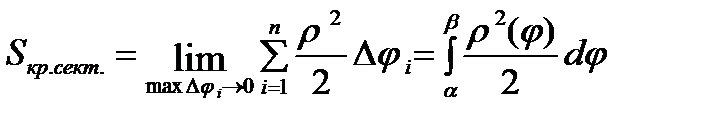
В ПСК: S=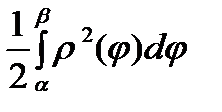 
.
Вычисление длины дуги кривой в декартовой системе координат.
Нужно вычислить длину плоской кривой L, заданной уравнением y=f(x) на отрезке [a,b].
Разобьем отрезок на части точками xi где i =0… n, a=x0<x1<x2<…<xn=b.
Через эти точки проведем прямые параллельные оси OY, которые разобьют кривую на n частей. Впишем в эти части ломаную.
Длина i-ого звена ломаной: Dl i= 
.
Просуммируем 
, сумма длин звеньев ломаной приближенно равна длине кривой. Переходя к пределу, получим: 
= 
= 
.
Пример: Вычислить длину полукубической параболы 
, где 
, x=0, x=1.
; 
.
.
Вычисление длины дуги кривой, заданной параметрически.
В декартовой системе координат длина дуги L= 
.
Предположим теперь, что кривая задана параметрически:
, 
, 
= 
.
Длина кривой заданной параметрически, выражается через определенный интеграл
L= 
.
Замечание: При вычислении длины кривой заданной параметрически нижний предел интегрирования должен быть меньше верхнего предела интегрирования.
Пример: Найти длину 1 арки циклоиды.
|
|
|
| Вычислим длину 1 арки циклоиды |
|
= 
= 
= 
= 
= 
= 
= 
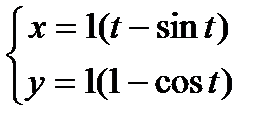
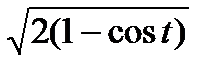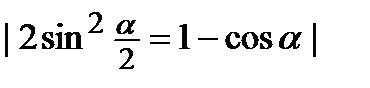L= 
= 
= 
= 
=-4(-1-1)=8.
|
|
|
