 |
Теорема о существовании определенного интеграла.
|
|
|
|
Если функция y=f(x) непрерывна на отрезке [a,b], то существует определенный интеграл 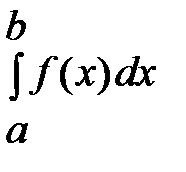 .
.
Замечание:
1. Определенный интеграл является числом.
2. Определенный интеграл зависит от a, от b, от f(x) и не зависит от переменной интегрирования.
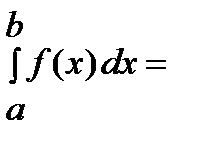
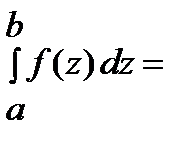
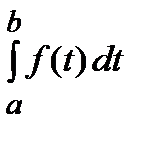 .
.
Свойства определенного интеграла.
Установим теперь, исходя из определения интеграла, его простейшие свойства. При этом подынтегральную функцию будем считать непрерывной.
1. Постоянный множитель можно выносить за знак определенного интеграла, т. е. если k — некоторое число, то 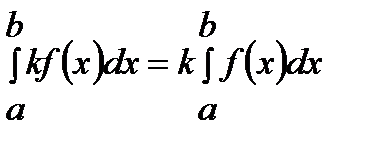 .
.
Действительно,

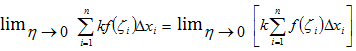 =
=
=k 
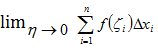 =k
=k 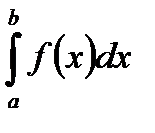 . (Здесь и далее
. (Здесь и далее  ).
).
2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от слагаемых.
Например, для двух слагаемых f(x) и g(x) имеем:
 .
.
Действительно, согласно определению интеграла имеем:
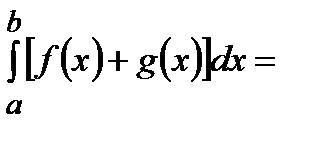
 =
= 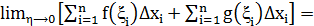
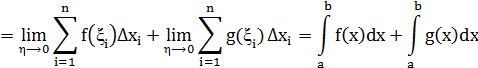
Совокупность свойств 1 и 2 называется свойством линейности.
3. Если сегмент интегрирования [a,b] разбит на две части [a,c] и [c,b], то
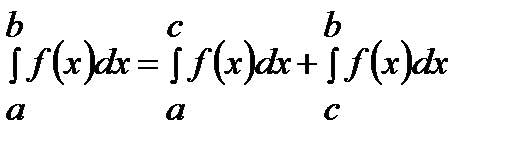 . (1)
. (1)
Действительно, предел интегральной суммы не зависит от способа разбиения сегмента [a,b] на части и от выбора промежуточных точек 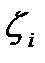 . Это позволяет при составлении каждой интегральной суммы включить точку сb число точек разбиения. Пусть
. Это позволяет при составлении каждой интегральной суммы включить точку сb число точек разбиения. Пусть 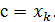 Тогда интегральная сумма будет состоять из двух частей, одна из которых относится к сегменту [a,c], а другая - к сегменту [c,b]:
Тогда интегральная сумма будет состоять из двух частей, одна из которых относится к сегменту [a,c], а другая - к сегменту [c,b]:
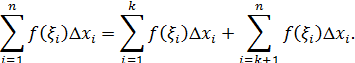
Переходя к пределу, получим
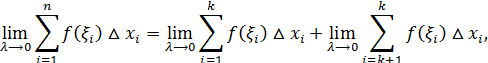
или 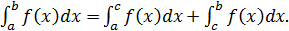 (Здесь
(Здесь 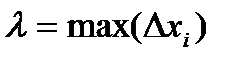 ).
).
Геометрически свойство 3 выражает тот факт, что площадь криволинейной трапеции с основанием [a,b] равна сумме площадей криволинейных трапеций с основаниями [a,c] и [c,b].
Замечание. Свойство 3 было нами сформулировано в предположении, что a<c<b. Однако равенство (1) имеет место для любых чисел a, b и c.
|
|
|
4. Если на сегменте [a,b]  , то
, то 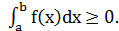
В самом деле, так как 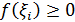 и
и 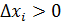 для любых i, то интегральная сумма
для любых i, то интегральная сумма 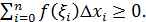 Поэтому и предел интегральной суммы при
Поэтому и предел интегральной суммы при 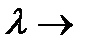
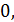 т.е.
т.е. 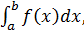 также неотрицателен.
также неотрицателен.
Можно доказать, что если на сегменте [a,b] непрерывная функция 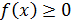 и хотя бы в одной точке этого сегмента
и хотя бы в одной точке этого сегмента 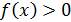 , то имеет место строгое неравенство
, то имеет место строгое неравенство 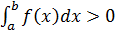 .
.
5. Если на сегменте [a,b] две функции f(x) и g(x) удовлетворяют неравенству  , то
, то 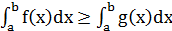 .
.
Иными словами, неравенство можно почленно интегрировать.
В самом деле, разность 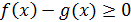 , поэтому согласно свойству 4
, поэтому согласно свойству 4 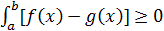 . Но так как согласно свойствам 1 и 2
. Но так как согласно свойствам 1 и 2

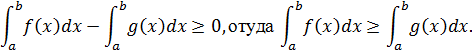
Это свойство имеет простой геометрический смысл. Пусть обе функции f(x) и g(x) являются неотрицательными на сегменте [a,b]. Тогда криволинейная трапеция, ограниченная кривой y=f(x), содержит криволинейную трапецию, ограниченную кривой y=g(x). Поэтому площадь первой фигуры не меньше площади второй фигуры. Исходя из геометрического смысла определенного интеграла, 
6. Теорема о среднем значении. Если f(x)-непрерывная на сегменте [a,b] функция, то существует такая точка ξ этого сегмента, что
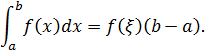
Обозначим через m и M соответственно наименьшее и наибольшее значение функции f(x) на сегменте [a,b]. Тогда для любого x,  выполняется неравенства
выполняется неравенства
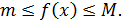 (2)
(2)
Применяя свойства 5 и 1, из неравенства (2) получим

Но 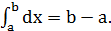 Следовательно,
Следовательно,
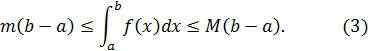
Разделив все члены двойного неравенства (3) на b-a, получим  , где
, где  . (4)
. (4)
Таким образом, число 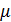 является промежуточным между наименьшим значением m функции f(x) и ее наибольшим значением M. Так как непрерывная на сегменте [a,b] функция f(x) принимает все промежуточные значения между m и M, то найдется такое значение ξ на сегменте [a,b], для которого f (ξ)=
является промежуточным между наименьшим значением m функции f(x) и ее наибольшим значением M. Так как непрерывная на сегменте [a,b] функция f(x) принимает все промежуточные значения между m и M, то найдется такое значение ξ на сегменте [a,b], для которого f (ξ)=  .
.
Подставляя в выражение (4) вместо 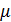 равное ему значение f (ξ), получим
равное ему значение f (ξ), получим
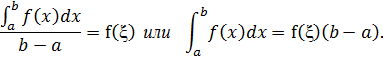
Итак, определенный интеграл от непрерывной функции равен значению подынтегральной функции в некоторой промежуточной точке, умноженному на длину сегмента интегрирования.
Итак, свойства определенного интеграла:
|
|
|
 f(x) и g (x)-непрерывны на [a,b] f(x) и g (x)-непрерывны на [a,b]
| ||
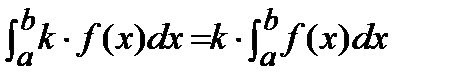 , k-const , k-const
| ||

| ||
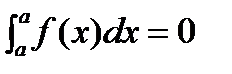
| ||

| ||
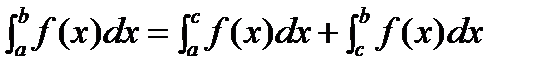
| ||
Если f(x)  и a≤b, то и a≤b, то 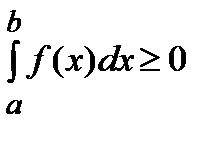
| ||
 , где m – наименьшее, M – наибольшее значение f(x) на [a;b] , где m – наименьшее, M – наибольшее значение f(x) на [a;b]
| ||
Существует точка СÎ [a,b] такая, что 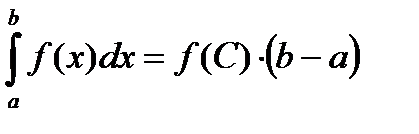 (f(x) -непрерывна)
(f(x) -непрерывна)
|
Интеграл с переменным верхним пределом и его производная.
Интегралом с переменным верхним пределом называется  .
.
Теорема: Если функция y=f(x) непрерывна, то 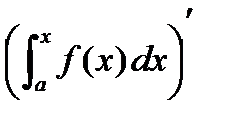 = f(x).
= f(x).
Возьмем точку x и вычислим в ней значение функции J(x) =  . Дадим x приращение Dx и вычислим значение функции.
. Дадим x приращение Dx и вычислим значение функции.
I(x+Dx) =  =
= 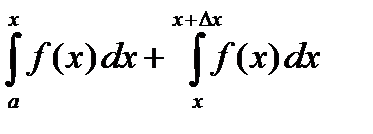 .
.
Функция I(x) получает приращение DI=I(x+Dx) – I(x)= 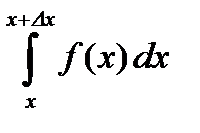
По теореме о среднем значении существует точка CÎ(x,x+Dx), такая что 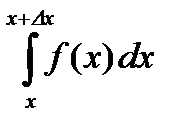 =
= 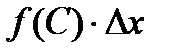 . Рассмотрим предел
. Рассмотрим предел  ,
,
т.к. при 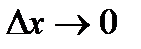
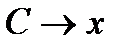 .
.
Из теоремы следует, что интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции.
У каждой непрерывной функции имеется первообразная (а значит, и неопределенный интеграл).
Формула Ньютона-Лейбница.
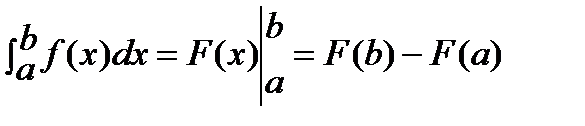 ,
,
где F(x) -одна из первообразных f(x).
Рассмотрим 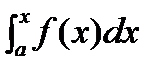 , он является одной из первообразных f(x), т.е.
, он является одной из первообразных f(x), т.е. 
 , где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=a Þ
, где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=a Þ 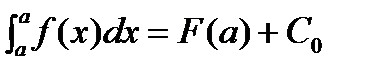 Þ C0=-F(a) Þ
Þ C0=-F(a) Þ 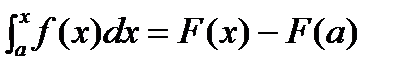 . Подставим вместо верхнего предела x=b Þ
. Подставим вместо верхнего предела x=b Þ 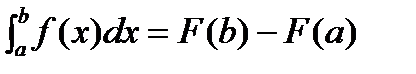
Формула позволяет вычислять определенный интеграл.
Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции. Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящее время. Хотя с процессом, аналогичным вычислению определенного интеграла как предела интегральной суммы, были знакомы еще в древности (Архимед), однако приложения этого метода ограничивались теми простейшими случаями, когда предел интегральной суммы мог быть вычислен непосредственно. Формула Ньютона-Лейбница значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т.д.
Пример:
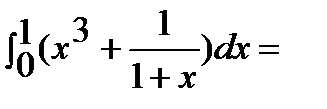
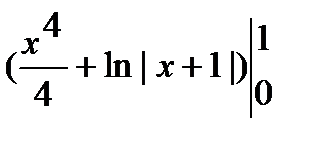

 .
.
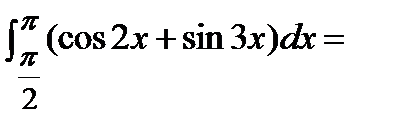

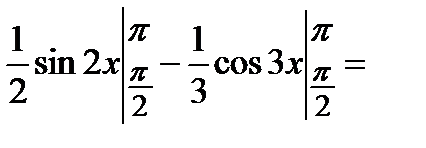
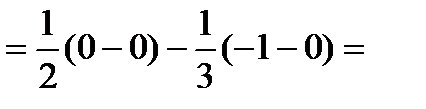
 .
.
|
|
|


