4. Выражения для потоков массы , энергии и импульса за счет различных механизмов.

4. Выражения для потоков массы, энергии и импульса за счет различных механизмов.

Конвективный механизм переноса массы

Поток массы за счет конвективного							механизма связан с			конвективной
скоростью
			w:

В случае многокомпонентной среды можно рассмотреть поток массы для каждого компонента:

где i – номер компонента; i - плотность компонента i.

Зачастую удобнее использовать поток вещества, а не массы:

где mi - мольная масса компонента i, ci – мольная концентрация.

Турбулентный механизм переноса массы

 

Турбулентный перенос массы можно рассматривать по аналогии с молекулярным как следствие хаотичного перемещения вихрей. Вместо коэффициента молекулярной диффузии вводится коэффициент турбулентной диффузии Dт и поток массы i-го компонента за счет турбулентной диффузии записывается в виде:

jiт DТ сi.			(2. 15. )
Если учесть, что молекулярная диффузия сохраняется и при турбулентной
диффузии можно записать:
ji = - (Di+Dт)		сi.	(2. 16. )

Поскольку объем среды, участвующие в турбулентных пульсациях, значительно превышают молекулярные размеры, интенсивность турбулентного переноса массы в пристенной области существенно выше молекулярного:

Dт 102 105,

Dм

При конвективном движении среды поток массы (или вещества) определяются как суммы конвективного и молекулярного переноса, а при турбулентном режиме к ним добавляют и турбулентную составляющую.

 Перенос энергии

Полную энергию системы на единицу массы можно записать:

Энергия может передаваться в виде теплоты или работы. Теплота – форма передачи энергии на микроуровне. Работа – форма передачи энергии на макроуровне.

 

5. Законы сохранения массы и энергии, их математическая запись в интегральной и локальной формах(уравнения, Фурье-Кирхгофа, Фурье, Фика).

Закон сохранение массы.

Суть закона: масса не может исчезать, либо возникать, т. е. суммарное количество массы в закрытой системе неизменно (закрытая не обменивается массой с окружающей средой).

Интегральная форма закона сохранения массы(материальный баланс). Изменение массы в некотором фиксированном объеме V вызывается разностью прихода и отвода из выделенного объема: , где V - изменение плотности.

-материальный баланс

Локальная форма закона сохранения массы (уравнение неразрывности). В локальной форме закон сохранения массы может быть сформулирован аналогично материальному балансу. Отличие заключается лишь в том, что в данном случае рассматривается не конечный объем V, а бесконечно малый dV.

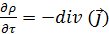-уравнение неразрывности

Для установившегося процесса: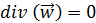

Общий поток:

Подставляя в уравнение неразрывности, получаем:

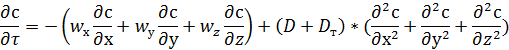
Для установившегося процесса:

Закон сохранения энергии.

- Тепловой баланс

Суть закона: изолированная система не обменивается с окружающей средой энергией, поэтому суммарная энергия этой системы постоянна.

Интегральня форма закона сохранения энергии. Изменение энергии в системе вызывается разностью ее прихода и расхода. Учитывая, что энергия может передаваться в форме теплоты Q и работы А, можно записать:

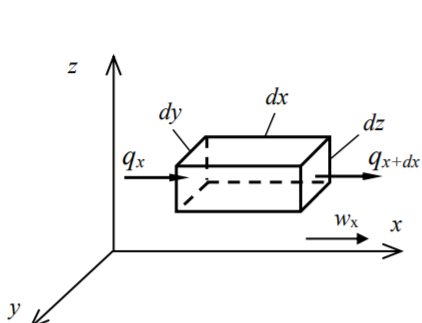
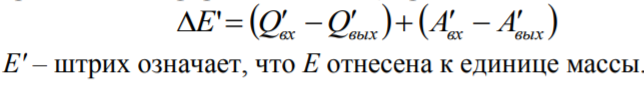
Локальная форма закона сохранения энергии.

Изменение плотности потока энергии по оси x в элементарном объеме dV.

Вывод уравнения, описывающего перенос энергии в движущейся среде, сводится к составлению энергетического баланса для элементарного объема жидкости dV=dxdydz.

уравнение Фурье-Кирхгофа, описывающее нестационарный процесс переноса энергии (теплоты) в движущейся среде , где  - коэффициент температуропроводности.

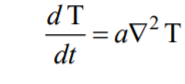При теплопереносе в неподвижной среде (w = 0) получим уравнение нестационарной теплопроводности Фурье (сокращение от уравнения Фурье-Кирхгофа):

Для случая стационарного переноса тепла в неподвижной среде получено:

Ñ ² *Т= 0.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: