Метод минимального числа ошибочных решений.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Юго-Западный государственный университет»

(ЮЗГУ)

Кафедра Космического приборостроения и систем связи

 

УТВЕРЖДАЮ Проректор по учебной работе __________О.Г. Локтионова «___»______________2016г.

 

 

ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЭЛЕКТРОННЫХ СРЕДСТВ

Методические рекомендации для проведению практических занятий для студентов направления подготовки 11.03.03 «Конструирование и технология электронных средств»

 

Курск 2016

 

УДК 678.029.983

 

Составитель: В.А. Пиккиев.

Рецензент

Кандидат технических наук, доцент О.Г. Бондарь

 

Техническая диагностика электронных средств: методические рекомендации для проведения практических занятий по дисциплине «Техническая диагностика электронных средств»/ Юго-Зап. гос. ун-т.; сост.: В.А. Пиккиев, Курск, 2016. 8с.: ил.4, табл.2, прилож.1. Библиогр.:с. 9.

 

 

Содержит методические рекомендации по изучению методов и алгоритмов технической диагностики электронных средств.

Методические рекомендации соответствуют требованиям программы, утвержденной учебно-методическим объединением по специальности Конструирование и технология электронных средств.

Методические указания для проведения практических занятий предназначены для студентов направления подготовки 11.03.03 «Конструирование и технология электронных средств».

 

Текст печатается в авторской редакции

 

Подписано в печать. Формат 60х84 1\16.

Усл. печ. л. Уч.-изд.л. Тираж 30 экз. Заказ. Бесплатно

Юго-Западный государственный университет.

305040, Курск, ул. 50 лет Октября,94.

 

 

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. ЦЕЛЬ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ.
1. Практическое занятие № 1. Метод минимального числа ошибочных решений
2. Практическое занятие № 2. Метод минимального риска
3. Практическое занятие № 3. Метод Байеса
4. Практическое занятие № 4. Метод наибольшего правдоподобия
5. Практическое занятие № 5. Метод минимакса
6. Практическое занятие № 6. Метод Неймана–Пирсона
7. Практическое занятие № 7. Линейные разделяющие функции
8. Практическое занятие № 8. Обобщенный алгоритм нахождения разделяющей гиперплоскости

 

 

ВВЕДЕНИЕ. ЦЕЛЬ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ.

Техническая диагностика рассматривает задачи диагностирования, принципы организации систем тестового и функционального диагноза, методы и процедуры алгоритмов диагноза для проверки неисправности, работоспособности и правильности функционирования, а также для поиска неисправностей различных технических объектов. Основное внимание уделяется логическим аспектам технической диагностики при детерминированных математических моделях диагноза.

Цель дисциплины состоит в освоении методов и алгоритмов технической диагностики.

Задачей курса является подготовка технических специалистов освоивших:

- современные методы и алгоритмы технической диагностики;

- модели объектов диагностирования и неисправностей;

- алгоритмы диагностирования и тесты;

- моделирование объектов;

- аппаратуру систем поэлементного диагностирования;

- сигнатурный анализ;

- системы автоматизации диагностирования РЭА и ЭВС;

- навыки разработки и построения моделей элементов.

Предусмотреные в учебном плане практические занятия, позволяют формировать у студентов профессиональные компетенции аналитического и творческого мышления путем приобретения практических навыков диагностики электронных средств.

Практические занятия предусматривают работу с прикладными задачами разработки алгоритмов поиска неисправностей электронных устройств и построению контролирующих тестов с целью их дальнейшего использования при моделировании функционирования этих устройств.

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

МЕТОД МИНИМАЛЬНОГО ЧИСЛА ОШИБОЧНЫХ РЕШЕНИЙ.

 

В задачах надежности рассматриваемый метод часто дает «неосторожные решения», так как последствия ошибочных решений существенно различаются между собой. Обычно цена пропуска дефекта существенно выше цены ложной тревоги. Если указанные стоимости приблизительно одинаковы (для дефектов с ограниченными последствиями, для некоторых задач контроля и др.), то применение метода вполне оправдано.

Вероятность ошибочного решения определяется так [1]

 

Где:

D₁- диагноз исправного состояния;

D₂- диагноз дефектного состояния;

P₁-вероятность 1 диагноза;

P₂- вероятность 2-го диагноза;

x₀- граничное значение диагностического параметра.

 

Из условия экстремума этой вероятности получаем

 

Условие минимума дает

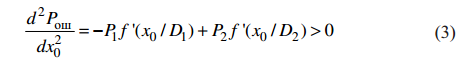
Или

 

Для одномодальных (т. е. содержат не более одной точки максимума) распределений неравенство (4) выполняется, и минимум вероятности ошибочного решения получается из соотношения (2)

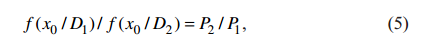
где, как и раньше, P₁= P(D₁), P₂= P(D₂) – априорные вероятности диагнозов.

Решение x ∈ D1 принимается при

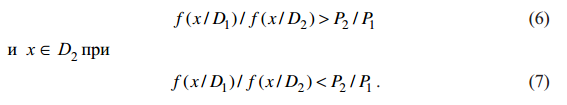
Условие выбора граничного значения (5) называется условием Зигерта–Котельникова (условием идеального наблюдателя). К этому условию приводит также метод Байеса.

Решение x ∈ D1 принимается при

что совпадает с равенством (6).

Рассеяние параметра (величина среднеквадратичного отклонения) принимается одинаковым.

В рассматриваемом случае плотности распределений будут равны:

(9)

Таким образом, полученные математические модели(8-9) могут быть использованы для диагностики ЭС.

Пример

Диагностика работоспособности жестких дисков осуществляется по количеству битых секторов (Reallocated sectors). Фирма Western Digital при производстве ЖД модели “My Passport” [2] использует следующие допуски: Исправными считаются диски у которых среднее значение составляет х₁ = 5 на единицу объема и среднеквадратичное отклонение σ₁ = 2. При наличии дефекта магнитного напыления (неисправное состояние) эти значения равны х₂ = 12, σ ₂ = 3. Распределения предполагаются нормальными.

Требуется определить предельное количество неисправных секторов, выше которого жесткий диск подлежит снятию с эксплуатации и разборке (во избежание опасных последствий). По статистическим данным, неисп­равное состояние магнитного напыления наблюдается у 10% ЖД.

Плотности распределения:

1. Плотность распределения для исправного состояния:

2. Плотность распределения для дефектного состояния:

 

 

3. Разделим плотности состояния и приравняем к вероятностям состояний:

 

 

4. Прологарифмируем данное равенство и найдем предельное количество неисправных секторов:

 

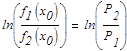
Это уравнение имеет положительный корень x₀ =9,79

Критическое количество битых секторов равно 9 на единицу объема.

Варианты задания

№ п/п	х1	σ 1	х2	σ 2

Вывод: Использование данного метода позволяет принимать решение без оценки последствий ошибок, из условий задачи.

Недостатком является то, что указанные стоимости приблизительно одинаковы.

Применение данного метода, распространено в приборостроение и машиностроении.

Практическое занятие № 2

МЕТОД МИНИМАЛЬНОГО РИСКА

Цель работы: изучение метода минимального риска для диагностики технического состояния ЭС.

Задачи работы:

- изучить теоретические основы метода минимального риска;

- провести практические расчеты;

- сделать выводы по использованию метода минимального риска ЭС.

Теоретические пояснения.

Вероятность принятия ошибочного решения слагается из вероятностей ложной тревоги и пропуска дефекта. Если приписать «цены» этим ошибкам, то получим выражение для среднего риск[1].

Где D1- диагноз исправного состояния; D2- диагноз дефектного состояния; P1-вероятность 1 диагноза; P2- вероятность 2-го диагноза; x0- граничное значение диагностического параметра; С12- стоимость ложной тревоги.

Разумеется, цена ошибки имеет условное значение, но она должна учесть предполагаемые последствия ложной тревоги и пропуска дефекта. В задачах надежности стоимость пропуска дефекта обычно существенно больше стоимости ложной тревоги (C12 >> C21). Иногда вводится цена правильных решений С11 и С22, которая для сравнения со стоимостью потерь (ошибок) принимается отрицательной. В общем случае средний риск (ожидаемая величина потери) выражается равенством

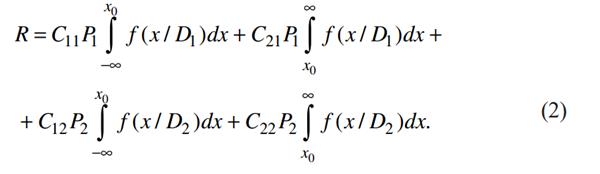
Где С11, С22 - цена правильных решений.

Величина x, предъявляемая для распознавания, является случайной и потому равенства (1) и (2) представляют собой среднее значение (математическое ожидание) риска.

Найдем граничное значение x0 из условия минимума среднего риска. Дифференцируя (2) по x0 и приравнивая производную нулю, получим сначала условие экстремума

Это условие часто определяет два значения x0, из которых одно соответствует минимуму, второе – максимуму риска (рис. 1). Соотношение (4) является необходимым, но недостаточным условием минимума. Для существования минимума R в точке x = x0 вторая производная должна быть положительной (4.1.), что приводит к следующему условию

(4.1.)

 

относительно производных плотностей распределений:

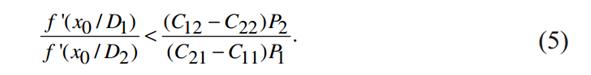
Если распределения f (x, D1) и f(x, D2) являются, как обычно, одномодальными (т. е. содержат не более одной точки максимума), то при

условие (5) выполняется. Действительно, в правой части равенства стоит положительная величина, а при x>x1 производная f '(x/D1), тогда как при x<x2 значение f '(x /D2).

В дальнейшем под x0 будем понимать граничное значение диагностического параметра, обеспечивающее по правилу (5) минимум среднего риска. Будем также считать распределения f (x / D1) и f (x / D2) одномодальными («одногорбыми»).

Из условия (4) следует, что решение об отнесении объекта x к состоянию D1 или D2 можно связать с величиной отношения правдоподобия. Напомним, что отношение плотностей вероятностей распределения x при двух состояниях называется отношением правдоподобия.

По методу минимального риска принимается следующее решение о состоянии объекта, имеющего данное значение параметра x:

(8.1.)

Эти условия вытекают из соотношений (5) и (4). Условие (7) соответствует x< x0, условие (8) x > x0. Величина (8.1.) представляет собой пороговое значение для отношения правдоподобия. Напомним, что диагноз D1 соответствует исправному состоянию, D2 – дефектному состоянию объекта; C21 – цена ложной тревоги; C12 – цена пропуска цели (первый индекс – принятое состояние, второй – действительное); C11 < 0, C22 – цены правильных решений (условные выигрыши). В большинстве практических задач условные выигрыши (поощрения) для правильных решений не вводятся и тогда

Часто оказывается удобным рассматривать не отношение правдоподобия, а логарифм этого отношения. Это не изменяет результата, таккак логарифмическая функция возрастает монотонно вместе со своимаргументом. Расчет для нормального и некоторых других распределений при использовании логарифма отношения правдоподобия оказывается несколько проще. Рассмотрим случай, когда параметр x имеет нормальное распределение при исправном D1 и неисправном D2 состояниях. Рассеяние параметра (величина среднеквадратичного отклонения) принимается одинаковым. В рассматриваемом случае плотности распределений

Внося эти соотношения в равенство (4), получаем после логарифмирования

Пример

Диагностика работоспособности флэш накопителей осуществляется по количеству битых секторов (Reallocated sectors). Фирма Toshiba TransMemory при производстве модели “UD-01G-T-03” использует следующие допуски: Исправными считаются накопители у которых среднее значение составляет х1 = 5 на единицу объема. Среднеквадратичное отклонение примем равным ϭ1 = 2.

При наличии дефекта NAND памяти эти значения равны х2 = 12, ϭ2 = 3. Распределения предполагаются нормальными. Требуется определить предельное количество неисправных секторов, выше которого жесткий диск подлежит снятию с эксплуатации. По статистическим данным, неисправное состояние наблюдается у 10% флэш накопителей.

Примем, что отношение стоимостей пропуска цели и ложной тревоги 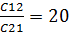, и откажемся от «вознаграждения» правильных решений (С11=С22=0). Из условия (4) получаем

 

Варианты задания:

Вар.

X1 мм.

X2 мм.

б1

б2

 

Вывод

Метод позволяет оценить вероятность принятия ошибочного решения определяется как минимизация точки экстремума среднего риска ошибочных решений при максимуме правдоподобия, т.е. проводится расчет минимального риска происхождения события при наличии информации о максимально подобных событиях.

 

 

ПРАКТИЧЕСКАЯ РАБОТА № 3

 

МЕТОД БАЙЕСА

 

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благодаря простоте и эффективности. Разумеется, метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако в случаях, когда объем статистических данных позволяет применить метод Байеса, его целесообразно использовать как один из наиболее надежных и эффективных.

Пусть имеется диагноз D_i и простой признак k_j, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния D_i и признака k_j)

(1)

Из этого равенства вытекает формула Байеса

(2)

Очень важно определить точный смысл всех входящих в эту формулу величин:

P(D_i) – вероятность диагноза D_i, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у N_i объектов имелось состояние D_i, то

(3)

P (k _j / D_i)– вероятность появления признакаk_jу объектов с состоянием D_i. Если среди N_i объектов, имеющих диагноз D_i, у N_ij, проявился признак k_j, то

(4)

P (k _j)– вероятность появления признакаk_jво всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак k_j был обнаружен у N_j объектов, тогда

(5)

Для установления диагноза специальное вычисление P(k_j) не требуется. Как будет ясно из дальнейшего, значения P(D_i) и P(k_j /D_v), известные для всех возможных состояний, определяют величину P(k_j).

В равенстве (2) P(D_i / k_j) – вероятность диагноза D_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность диагноза).

Обобщенная формула Байеса относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k₁, k₂, …, k_ν. Каждый из признаков k_j имеет m_j разрядов (k_j1, k_j2, …, k_js, …, k_jm). В результате обследования становится известной реализация признака

(6)

и всего комплекса признаков К^*. Индекс ^*, как и раньше, означает конкретное значение (реализацию) признака. Формула Байеса для комплекса признаков имеет вид

(7)

где P(D_i / K^*) – вероятность диагноза D_i после того, как стали известны результаты обследования по комплексу признаков K; P(D_i) – предварительная вероятность диагноза D_i (по предшествующей статистике).

Формула (7) относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

(8)

В практических задачах нередко допускается возможность существования нескольких состояний A₁, …, A_r, причем некоторые из них могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов D_i следует рассматривать отдельные состояния D₁ = A₁, …, D_r = A_r и их комбинации D_r+1 = A₁ /\ A₂.

Перейдем к определению P (K ^* / D_i). Если комплекс признаков состоит из н признаков, то

(9)

где k ^* _j = k _js – разряд признака, выявившийся в результате обследования. Для диагностически независимых признаков;

(10)

В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними.

Вероятность появления комплекса признаков K^*

(11)

Обобщенная формула Байеса может быть записана

(12)

где P(K^* / D_i) определяется равенством (9) или (10). Из соотношения (12) вытекает

 

(13)

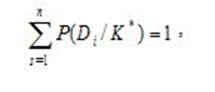
что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация одновременно двух диагнозов невозможна.

Следует обратить внимание на то, что знаменатель формулы Байеса для всех диагнозов одинаков. Это позволяет сначала определить вероятности совместного появления i-го диагноза и данной реализации комплекса признаков

(14)

и затем апостериорную вероятность диагноза

(15)

Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу (табл. 1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков при различных диагнозах.

 

Таблица 1

Если признаки двухразрядные (простые признаки «да – нет»), то в таблице достаточно указать вероятность появления признака P(k_j / D_i).

Вероятность отсутствия признака P (k j / D_i) = 1 − P (k _j / D_i).

Однако более удобно использовать единообразную форму, полагая, например, для двухразрядного признака P (kj / D) = P (kj 1/ D); P (k j / D) = P (kj 2/ D).

Отметим, что ∑ P (k _js / D_i) =1, где m_j – число разрядов признака k_j.

Сумма вероятностей всех возможных реализаций признака равна единице.

В диагностическую матрицу включены априорные вероятности диагнозов. Процесс обучения в методе Байеса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти ЭВМ следует хранить не только значения P(k_js / D_i), но и следующие величины: N – общее число объектов, использованных для составления диагностической матрицы; N_i — число объектов с диагнозом D_i; N_ij – число объектов с диагнозом D_i, обследованных по признаку k_j. Если поступает новый объект с диагнозом D_μ, то проводится корректировка прежних априорных вероятностей диагнозов следующим образом:

(16)

Далее вводятся поправки к вероятностям признаков. Пусть у нового объекта с диагнозом D_μ выявлен разряд r признака k_j. Тогда для дальнейшей диагностики принимаются новые значения вероятности интервалов признака k_j при диагнозе D_μ:

(17)

Условные вероятности признаков при других диагнозах корректировки не требуют.

 

Практическая часть

1.Изучить методические указания и получить задание.

2. Рассчитать вероятность указанного преподавателем диагноза (технического состояния исследуемого объекта) при появлении определенных диагностических параметров.

 

ПРАКТИЧЕСКАЯ РАБОТА № 4

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: