 |
Задание к практической работе
|
|
|
|
Исправное состояние ШИМ-контроллев D1 характеризуется пониженной температурой и повышенным временем выхода на определенную температуру по сравнению с неисправным состоянием D2.
Построить линейную разделяющую функцию для диагностики ШИМ-контроллев на два класса. Измерения t0 и t выхода для экземпляров, находящихся в состоянии D1 и D2, представлены в табл. 1
Таблица 1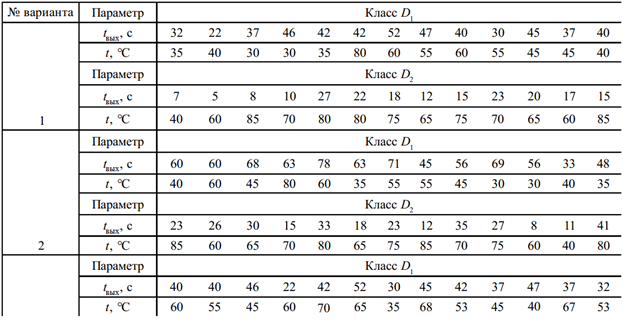 
Пример расчета варианта 2
Исходные данные
| 
| 
| 
|
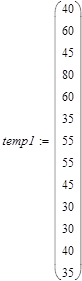
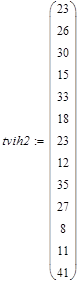
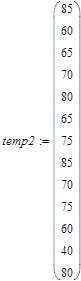
Формулы для расчета
| 
|
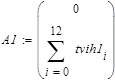
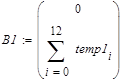
| Координаты суммарного вектора первого облака значений | |
| 
|
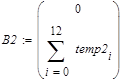
| Координаты суммарного вектора второго облака значений | |
| 
|
| Координаты вектора проекции разделяющий плоскости | |
| 
|
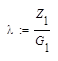
| Нормирующий коэффициент | Уравнение разделяющей функции |
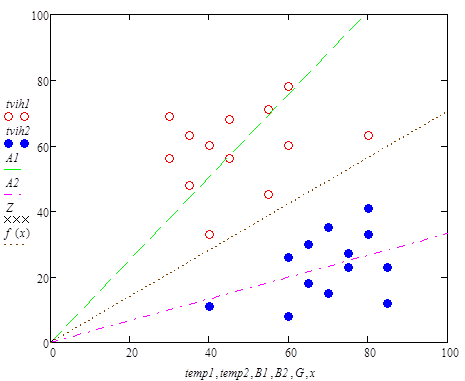
График разделяющей функции
Красные выколотые точки - облако нерабочих значений.
Синие точки - облако рабочих состояний.
Зеленый и розовый пунктиры суммарные вектора первого и второго облака значений.
Черный пунктир - вектор проекции разделяющей плоскости.
В рассмотренном примере разделяющая функция была построена в координатах температуры и времени.
Выводы
Метод может использоваться в алгоритмах распознавания образов и звуков, в скоростном обучении нейросетей. В технической диагностике может применятся для разделение большого количества экспериментальных данных на две группы.
При большом количестве измерений по нескольким параметрам способ линейной дискриминантой функции позволяет отделить параметры вышедшие за пределы нормы, не зная критические значений контролируемых параметров. В рассмотренном примере разделяющая функция показывает крайние значения рабочих/нерабочих состояний контролируемых изделий. При помощи этого разделения становится возможным произвести быстрое разделения рабочих и нерабочих образцов, не перестраивая плоскость.
|
|
|
Главным недостатком метода линейных разделяющих функций является то, что при погружении части значений одного множества в другое, становится невозможным использовать линейные функции для построения разделяющей плоскости.
ПРАКТИЧЕСКАЯ РАБОТА №8
ОБОБЩЕННЫЙ АЛГОРИТМ НАХОЖДЕНИЯ
РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Метод нахождения разделяющей гиперплоскости, которые будут рассматриваться в данной практической работе, предназначены для непосредственного решения задач диагностики состояния электронных средств по признакам работоспособного состояния.
Разделяющая гиперплоскость — гиперплоскость, разделяющая два выпуклыхмножества, каждое из которых лежит в одном из двух полупространств, образуемых этой гиперплоскостью в многомерном пространстве. Два замкнутых ограниченных выпуклых множества, не имеющих общих точек, всегда могут быть разделены гиперплоскостью. Причем если эти множества пересекаются в единственной точке, единственная разделяющая их гиперплоскость является также опорной гиперплоскостью для обоих множеств.
Рисунок 1. Весовой вектор и разделяющая гиперплоскость
Разделяющая гиперплоскость проходит через начало координат (в дополненном пространстве признаков) и нормальна весовому вектору λ. Следовательно, вектор λ однозначно определяет положение разделяющей плоскости в пространстве признаков и задача сводится к нахождению вектора λ.
Рассмотрим обобщенный алгоритм нахождения весового вектора с помощью показа образцов из обучающей последовательности. Будем считать, что векторы объектов x принадлежат объединенной области диагнозов D, т. е.
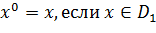(1)
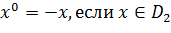
Используемая ранее процедура для векторов объединенной области, имеет вид
|
|
|
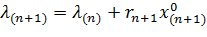(2)
где
В обобщенном алгоритме используется прежняя процедура нахождения вектора λ, но выбор скалярного корректирующего множителя r подчинен другим условиям.
Пусть построен вектор λ(n) и соответствующая разделяющая плоскость, но образец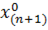 
распознается неправильно: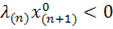 
Проведем корректировку вектора λ(n) так, чтобы новое положение разделяющей плоскости давало правильное распознавание объекта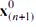 
Тогда по соотношению (2)
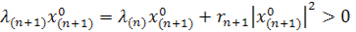(4)
или
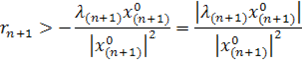(5)
Если же объект 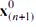распознается достоверно, то корректировки
вектора λ(n) не требуется и следует положить 
. Примем обобщенный алгоритм нахождения весового вектора в такой форме
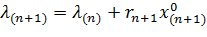(6)
где
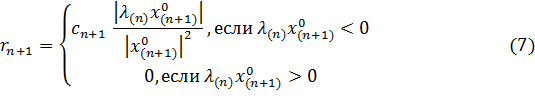
Здесь — скалярный множитель, соответствующий (n + 1)-му
приближению. Если положить
то получается указанный ранее алгоритм. Установим достаточное условие, обеспечивающее приближение к точному решению в процессе последовательных приближений. Пусть λ представляет собой точное значение весового (разделяющего) вектора
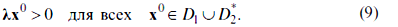
Вычитая из обеих частей равенства (6) вектор λ и умножая скаляр-
но обе части равенства на себя, получим
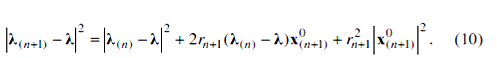
Последнее соотношение представим так:
Очевидно, что при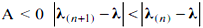 
и при возрастании n (увеличении числа исправлений) процесс сходится к точному значению
λ(n) →λ. Таким образом, достаточное условие сходимости
A < 0. (12)
|
|
|
