 |
Линейные разделяющие функции
|
|
|
|
Метод Разделяющих функций, которые будут рассматриваться в данной практической работе, предназначены для непосредственного решения задач диагностики состояний ЭС по признакам работоспособного состояния.
Один из важнейших классов разделяющих функций связан с линейными дискриминантными функциями. Тогда разделяющая функция при распознавании двух классов:
Величины λj называются весовыми коэффициентами. Методы распознавания с помощью линейных разделяющих функций называются
линейными методами разделения. Диагнозы, для которых возможно
такое распознавание, считаются линейно-разделимыми.
Весовые коэффициенты λj образуют весовой вектор с числом компонентов N + 1
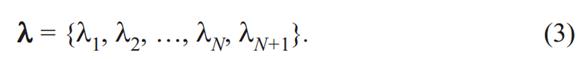
Для удобства геометрической интерпретации дополним вектор х еще
одним компонентом
Тогда дополненный вектор признаков
Разделяющую функцию при диагностике на два состояния можно
представить в виде скалярной суммы
Условия разделения (решающее правило):
Разделяющая поверхность является плоскостью в (N + 1)-мерном
пространстве или гиперплоскостью. Уравнение разделяющей гиперплоскости
Уравнение (8) означает, что весовой вектор λ перпендикулярен разделяющей гиперплоскости (рис. 1). В дополненном пространстве признаков разделяющая гиперплоскость всегда проходит через начало координат.
Линейная разделяющая функция в дополненном пространстве признаков имеет простой геометрический смысл f(x*) = λx* = h, где h –проекции вектора x* на направление весового вектора λ, что вытекаетиз смысла скалярной суммы. Абсолютная величина h равна расстоянию точки x* до разделяющей плоскости λx* = 0. Значение h положительно, если точка *x находится в полупространстве, векторы точеккоторого дают положительную проекцию на вектор λ.
|
|
|
Нахождение разделяющей гиперплоскости. Разделяющая гиперплоскость проходит через начало координат (в дополненном пространстве признаков) и нормальна весовому вектору λ. Следовательно, вектор λ однозначно определяет положение разделяющей плоскости в пространстве признаков и задача сводится к нахождению вектора λ.
Рассмотрим процедуру определения весового вектора с помощью обучающей последовательности. Под обучающей последовательностью понимается совокупность образцов с известным диагнозом (совокупность «верифицированных образцов»). Эта последовательность используется для «обучения», в данном случае – нахождения весового вектора (разделяющей гиперплоскости).
Пусть в пространстве признаков имеются две области диагнозов D1 иD2. Они изображены для трехмерного пространства признаков на рис. 2.Разделяющая плоскость должна удовлетворять условиям (7), которые можно упростить, если ввести в рассмотрение объединенную область диагнозов 
, где D2* – область диагноза D2, симметрично отображенная относительно начала координат (рис. 3). Знак ∪ означает объединение множеств. Область D2* получается из D2, если знак у векторов D∈x изменить на противоположный. Отметим, что области D1 и D2* могут иметь общие точки. Теперь разделяющая функция вместо соотношений (7) будет удовлетворять условию
Следовательно, объединенная область D должна располагаться по одну сторону от разделяющей гиперплоскости (8) или, что равносильно, гиперплоскость не должна пересекать объединенную область диагноза. В дальнейшем придется часто рассматривать векторы в дополненном пространстве (xN+1 = 1) признаков и для простоты опустим индекс* у вектора х. Уравнение гиперплоскости запишем так:
При определении вектора λ применяется процедура последовательных приближений. Для обучения предъявляется первый образец x(1), относительно которого диагноз известен. В качестве первого приближения: для вектора λ принимается
|
|
|
На рис. 4 показан случай, когда первый образец принадлежит области D2. Разделяющая плоскость для первого приближения описывается уравнением
т. е. разделяющая плоскость перпендикулярна вектору первой точки. Далее предъявляется второй образец, описываемый вектором x(2). На рис. 4 этот образец относится к диагнозу D1. Сначала проверяется правильность предыдущего приближения для разделяющей плоскости. Если выполняется условие λ(1)x(2) > 0, то весовой вектор не требует корректировки и во втором приближении принимается λ(2) = λ(1).
Случай, когда во втором приближении не требуется внесения поправки,
показан на рис. 4
Далее предъявляется третий образец x(3) и проводится проверка предыдущего значения весового вектора. Если λ(2)x(3) > 0, то исправления вектора не требуется и принимается λ(3) = λ(2) (точки x(1), x(2), x(3) лежат по одну сторону от разделяющей плоскости). Если λ(2)x(3) > 0 (этот случай показан на рис. 4), то условие разделения (9) λx > 0 не выполняется и требуется скорректировать весовой вектор. Принимают теперь λ(3) = λ(2) + x(3) и далее переходят к показу следующего образца. В общем виде описанную процедуру можно представить так:
В последнем равенстве:
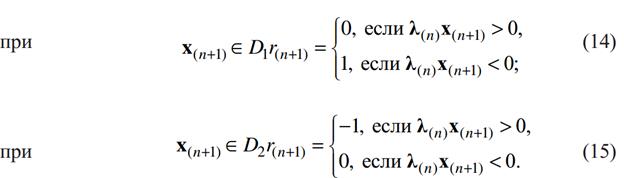
Иными словами, при неправильных ответах к вектору λ(n) добавляется вектор точки, относительно которой была совершена ошибка.
|
|
|
