Метод наибольшего правдоподобия

 

Метод наибольшего правдоподобия можно рассматривать как част­ный случай метода минимального риска [1]. Правило решения принимает­ся следующим:

 

где: x - значение параметра для диагностируемого объекта.

D₁ – диагноз исправного состояния;

D₂ – диагноз дефектного состояния.

 

Граничное значение X₀ находится из условия

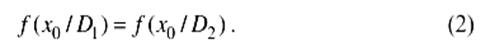
где: Х₀ – граничное значение диагностического параметра

 

В большинстве практических случаев используется условие (3)

где: С₁₂ – цена пропуска дефекта;

С₂₁ – цена ложной тревоги;

С₂₂, С₁₁ – цены правильных решений;

Р₁ – вероятность первого диагноза;

Р₂ – вероятность второго диагноза.

В данном методе, цены правильных решений принимаются равными нулю, так как производитель не несет дополнительных затрат, и тогда для метода наибольшего правдоподобия следует считать

 

Для задач надежности вероятность неисправного состояния обычно представляет собой малую величину, но цена пропуска дефекта значи­тельно больше цены ложной тревоги (C₁₂ >> C₂₁). Тогда условие (4) дает решение, не требующее знания точных значений стоимости оши­бок и качественно отражающее указанные обстоятельства (P₂ << Р_х, C₁₂ >> C_2l).

 

Пример

Одним из параметров низкочастотных динамических головок является величина линейного хода, значение этого параметра при подаче тестового сигнала не должно превышать паспортное.

Рассмотрим на примере динамических головок модели Урал АК-10.

Величина линейного хода у исправного образца х₁ = 5 мм. Экспериментальные значения для расчета ср.кв. отклонения 6,5; 5; 6; 2; 8.

Величина линейного хода у неисправного образца х₂ = 12 мм.

Экспериментальные значения для расчета ср.кв. отклонения 15;8;12;16;15,55.

(данные для расчета получены в ходе эксперимента по исследованию НЧ головок)

Распределения предполагаются нормальными.

Требуется определить предельное значение величины линейного хода.

 

Примем, что (С₁₁=С₂₂= 0)

С помощью системы Mathcad найдем ср. квадратичное отклонение:

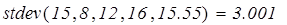
Плотности распределений равны:

 

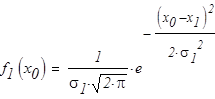
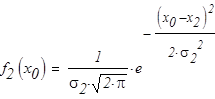
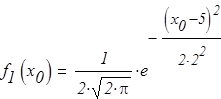
Отношений плотностей распределения равно:

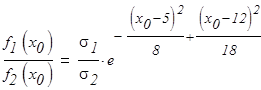
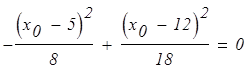
Это уравнение имеет положительный корень x₀ = 7,8.

Таким образом, на основе метода определено критическое значение линейного хода диффузора равно 7,8мм.

 

Вывод

Этот метод является частным случаем метода минимального риска и его можно использовать для оценки критического значения параметра (например хода диффузора). Метод позволяет оценить критическое значение параметра в ситуациях, когда вознаграждение (стоимость или цена) за принятие верного решения равно нулю, что является его недостатком.

 

Варианты задания:

Вар.

X1 мм.

X2 мм.

б1

б2

 

ПРАКТИЧЕСКАЯ РАБОТА № 5

МЕТОД МИНИМАКСА

Метод минимакса предназначен для ситуации, когда отсутствуют предварительные статистические сведения о вероятности диагнозов D₁ и D₂. Рассматривается «наихудший случай», т. е. наименее благоприятные значения P₁ и P₂, приводящие к наибольшему значению (максимуму) риска.

 

Будем считать, что величина риска зависит теперь от x₀ и P₁ (вероятность второго диагноза P₂ = 1 – P₁). Из соотношения вытекает, что

 

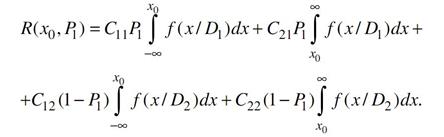
Для нахождения экстремума приравняем нулю частные производные по x₀ и P₁. Условие

дает

Из соотношения

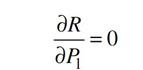
получаем

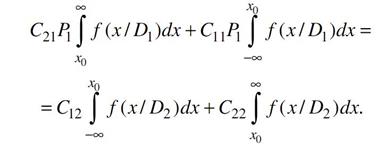
Теперь требуется определить значения x₀ и P₁, удовлетворяющие уравнениям (3) и (5). Если x ₀^* и P ₁^* являются корнями указанных уравнений, то точка R (x ₀^*, P ₁^*) является экстремальной.

Можно показать для одномодальных распределений, что величина риска становится минимаксной (т. е. минимальной среди максимальных значений, вызванных «неблагоприятной» величиной P₁). Отметим, что при P₁ = 0 и P₂ = 1 риск принятия ошибочного решения отсутствует, так как ситуация не имеет неопределенности. При P₁ = 0 (все изделия неисправны) из условия (4) вытекает x ₀ → −∞ и все объекты действительно признаются неисправными; при P₁ = 1 и P₂ = 0 x ₀ →∞ и в соответствии с имеющейся ситуацией все объекты классифицируются как исправные.

Для промежуточных значений 0 < P₁ < 1 риск возрастает и при P ₁ = P ₁^* становится максимальным. Рассматриваемым методом выбирают величину x₀ таким образом, чтобы при наименее благоприятных значениях P₁ потери, связанные с ошибочными решениями, были бы минимальными.

Рассмотрим процедуру решения уравнений (3) и (5). Сначала из уравнения (5) найдем значение x ₀^*, что можно сделать следующим образом. Представим уравнение (5) в виде

где

Последнее равенство можно записать с помощью функций распределения

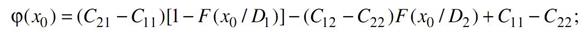
Уравнение (6) решаем по методу Ньютона, связывающему исходные x_0(n–1) и последующие x_0(n) приближения

Значение производной

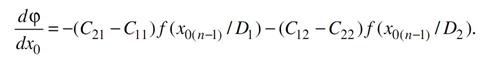
В качестве первого приближения можно принять x ₀₍₁₎ = (x ₁ = x ₂) / 2, где x ₁, x ₂ – средние значения х для распределения f(x / D₁) и f(x / D₂). При достаточной близости x_0(n) и x_0(n–1) принимаем x ₀^* = x _{0( n )}. Далее из равенства (3) находим наименее благоприятное значение вероятностей исправного P⁸ и P⁸ неисправного состояния

 

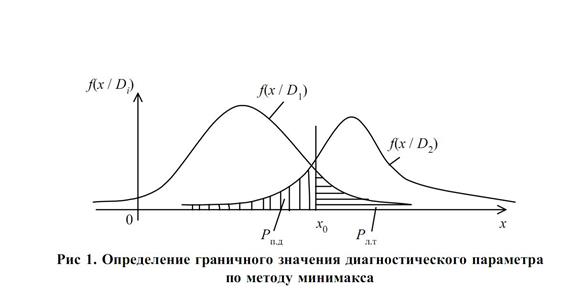
Величину риска определяем по равенству (1) при значениях x ₀  x ₀^*,

P ₁= P ₁^*. Отметим некоторые случаи, в которых решение становится достаточно наглядным. Положим, что условные выигрыши отсутствуют C₁₁ = C₂₂ = 0, а цены ошибок одинаковы C₁₂ = C₂₁. Тогда из уравнения (5) вытекает

где F(x₀ / D₁) и F(x₀ / D₂) – соответствующие функции распределения. Последнее соотношение показывает равенство условных вероятностей ошибочных решений.

На рис. 1 для этого случая площади P_л.т и P_п.д равны. В общем случае

Зависимость (12) выражает равенство условных рисков ошибочных решений. С помощью функций распределения она записывается в виде

 

Практическая часть

1. Изучить методические указания и получить задание.

2. Рассчитать предельное значение диагностического параметра, выше которого исследуемый объект подлежит снятию с эксплуатации по методу минимакса.

ПРАКТИЧЕСКАЯ РАБОТА № 6

МЕТОД НЕЙМАНА–ПИРСОНА

Принципы выбора критической области были сформулированы Нейманом и Пирсоном. Суть критерия Неймана — Пирсона состоит в следующем. Исходя из того, какие решения принимаются на основании результатов распознавания неизвестных объектов, определяется допустимое (заданное) значение условной вероятности ошибки первого рода Q₁, затем определяется такая граница между классами, придерживаясь которой удается добиться минимума условной вероятности ошибки второго рода.

Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием (в информационных технологиях часто используют английский термин false positive без перевода). Соответственно, ошибку второго рода иногда называют пропуском события (в информационных технологиях часто используют английский термин false negativ).

Допустимая условная вероятность ошибки первого рода не должна превышать некоторой постоянной величины А, т. е. Q₁≤А. Требуется определить решение х₀ задачи

(1)

при ограничениях вида

(2)

Очевидно, что решение х₀ удовлетворяет уравнению

. (3)

Так как при выборе другого значения условная вероятность ошибок второго рода Q₂ возрастает. Выбрать же 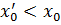нельзя по условиям задачи.

ПРИМЕР

Пусть у вентиляторов всех типов параметры α и β соответственно подчинены нормальным законам распределений. При этом у вентиляторов типа А первое состояние характеризуется следующими значениями математического ожидания и среднеквадратичного отклонения:

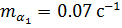; ; второе состояние — значениями 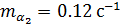; ; 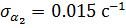аналогично, у вентиляторов типа В первое состояние характеризуется значениями ; ; 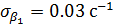второе состояние — значениями ;

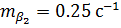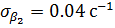
На рисунке 1 представлены законы р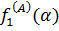аспределений , , а на рисунке 2 — законы распределений , [3].

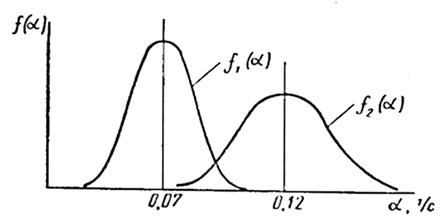
Рисунок 1 – Законы распределений ,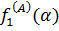

Рисунок 2 – Законы распределений ,

Будем полагать, что изменение интенсивности звука работающего вентилятора во времени – случайный стационарный процесс. Нормированная корреляционная функция этого процесса может быть аппроксимирована уравнением вида 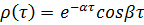. Рассмотрим типы А и В вентиляторов, различая у каждого из типов состояния: 1) вентилятор исправен; 2) вентилятор неисправен. У вентиляторов типа А признак, характеризующий их состояние, – параметр α, у вентиляторов типа В – параметр β [3].

Исходные данные

Определим граничные значения и 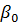для вентиляторов типов А и В на основе критерия Неймана – Пирсона, полагая, что ошибка первого рода не должна превышать 5% [2].

 

 

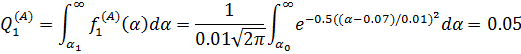
Отсюда 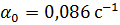. Ошибка второго рода при этом

Аналогичные расчеты для вентиляторов типа В дают значения 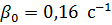и .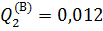

Таким образом, были определены граничные значения и 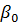, означающие вероятность ошибок второго рода, а также ошибки второго рода для вентиляторов типа А и В, означающие пропуск информации о вентиляторе, как о нормально работающем при наличии сбоев в работе.

Выводы

Во многих случаях в технической диагностике ЭС оптимальной моделью распознавания образов двух классов считают такую модель, которая реализует минимум вероятности ошибки одного вида при данном значении вероятности ошибки другого вида. Условие минимума вероятности ошибки одного вида при заданной вероятности ошибки другого вида обычно называется критерием Неймана-Пирсона. Этот критерий получил широкое применение в области диагностики компьютерных систем, их программного обеспечения, а также в системах радиолокации, биометрии и др. Его отличительным преимуществом является простота расчета и широкая область применения.

Варианты заданий

Вариант	,	,	,	,	,	,	,	,	, %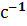
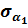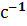
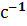
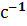
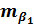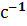
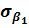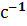
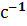
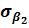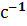
	0.072	0.012	0.122	0.017	0.112	0.032	0.252	0.042	5.5
	0.074	0.014	0.126	0.019	0.114	0.034	0.254	0.044
	0.076	0.016	0.128	0.021	0.116	0.036	0.256	0.046	6.5
	0.078	0.018	0.130	0.023	0.118	0.038	0.258	0.048
	0.080	0.020	0.132	0.025	0.120	0.040	0.260	0.050	7.5
	0.075	0.015	0.125	0.020	0.115	0.035	0.300	0.045	6.5
	0.077	0.017	0.127	0.022	0.117	0.037	0.302	0.047
	0.079	0.019	0.129	0.024	0.119	0.039	0.304	0.049	7.5
	0.081	0.021	0.131	0.026	0.121	0.041	0.306	0.051
	0.083	0.023	0.133	0.028	0.123	0.043	0.308	0.053	8.5

ПРАКТИЧЕСКАЯ РАБОТА № 7

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: