 |
Системы сложных сигналов для телекоммуникационных систем
|
|
|
|
Спектры сигналов
Спектр сигнала s(t) определяется преобразованием Фурье
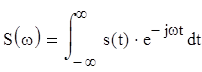
В общем случае спектр является комплексной функцией частоты ω. Спектр может быть представлен в виде
,
где |S(ω)| – амплитудный, а φ(ω) – фазовый спектр сигнала s(t).
Спектр сигнала обладает следующими свойствами:
1. Линейность: если имеется совокупность сигналов s1(t), s2(t), …, причем s1(t)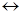 
S1(ω), s2(t) 
S2(ω), …, то сумма сигналов преобразуется по Фурье следующим образом:
,
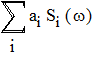где ai – произвольные числовые коэффициенты.
2. Если сигналу s(t) соответствует спектр S(ω), то такому же сигналу, смещенному на t0, соответствует спектр S(ω) умноженный на e-jωt0 s(t-t0) 
S(ω)e-jωt0.
3. Если s(t)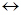 
S(ω), то
4. Если s(t) 
S(ω) и f(t)=ds/dt, то f(t) F(ω)=jωS(ω).
5. Если s(t)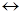 
S(ω) и g(t)=∫s(t)dt, то g(t) 
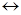G(ω)=S(ω)/jω.
6. Если u(t) 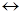U(ω), v(t) V(ω) и s(t)=u(t)v(t), то
.
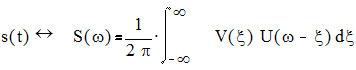Сигнал находится по спектру с помощью обратного преобразования Фурье
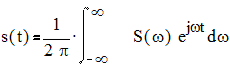.[4]
Рассмотрим спектры некоторых сигналов.
Прямоугольный импульс.
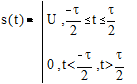
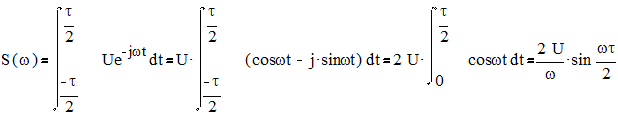
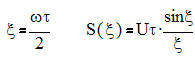
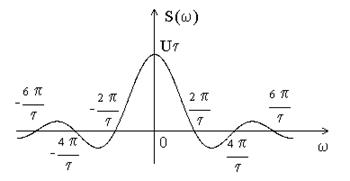
Рис.2.1. Спектр прямоугольного импульса.
Гауссовский импульс.
s(t)=Uexp(-βt2)
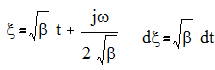
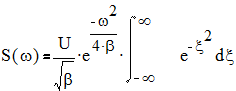
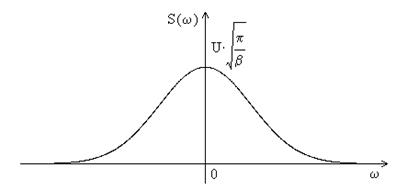
Рис.2.2. Спектр гауссовского импульса.
Сглаженный импульс
С помощью численного интегрирования находим спектр S(ω).
S(0)=2.052 S(6)=-0.056
S(1)=1.66 S(7)=0.057
S(2)=0.803 S(8)=0.072
S(3)= 0.06 S(9)=0.033
S(4)=-0.259 S(10)=-0.0072
S(5)=-0.221 S(ω)=S(-ω)
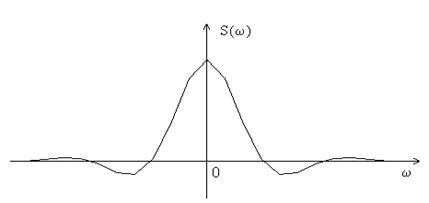
Рис. 2.3. Спектр сглаженного импульса.
Корреляционные свойства сигналов
Для сравнения сигналов, сдвинутых во времени, вводят автокорреляционную функцию (АКФ) сигнала. Она количественно определяет степень отличия сигнала u(t) и его смещенной во времени копии u(t - τ) и равна скалярному произведению сигнала и копии:
|
|
|
Непосредственно видно, что при τ=0 автокорреляционная функция становится равной энергии сигнала: Bu(0)=Eu.
Автокорреляционная функция четна: Bu(τ)=Bu(-τ).
При любом значении временного сдвига τ модуль АКФ не превосходит энергии сигнала |Вu(τ)|≤Bu(0)=Eu.
АКФ связана со спектром сигнала следующим соотношением:
.
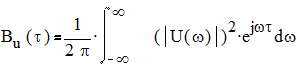Верно и обратное:
.
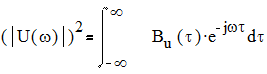Для дискретного сигнала АКФ определяется в следующем виде:
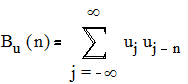
и обладает следующими свойствами.
Дискретная АКФ четна: Bu(n)=Bu(-n).
При нулевом сдвиге АКФ определяет энергию дискретного сигнала:
.
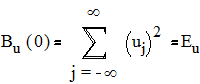Иногда вводят взаимнокорреляционную функцию (ВКФ) сигналов, которая описывает не только сдвиг сигналов друг относительно друга по времени, но и различие в форме сигналов.
ВКФ определяется следующим образом
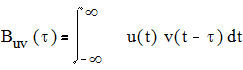
для непрерывных сигналов и
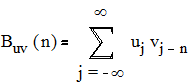
для дискретных сигналов. [4]
Рассмотрим АКФ некоторых сигналов.
Последовательность прямоугольных импульсов
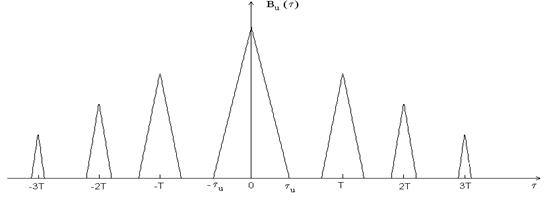
Рис. 2.4. АКФ последовательности прямоугольных импульсов.
Позиционный сигнал Баркера
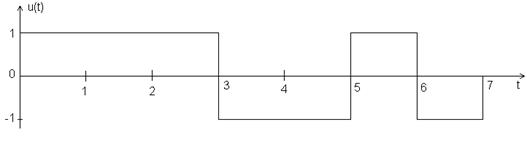
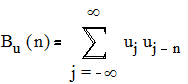
Bu(0)=7, Bu(1)= Bu(-1)=0, Bu(2)= Bu(-2)=-1, Bu(3)= Bu(-3)=0, Bu(4)= Bu(-4)=-1, Bu(5)= Bu(-5)=0, Bu(6)= Bu(-6)=-1, Bu(7)= Bu(-7)=0.
Рис. 2.5. АКФ 7-позиционного сигнала Баркера.
Позиционные функции Уолша
Функция Уолша 2-го порядка
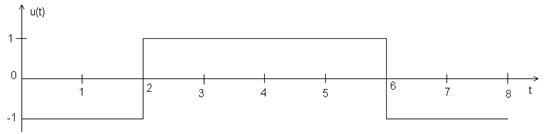
Bu(0)=8, Bu(1)= Bu(-1)=3, Bu(2)= Bu(-2)=-2, Bu(3)= Bu(-3)=-3, Bu(4)= Bu(-4)=-4, Bu(5)= Bu(-5)=-1, Bu(6)= Bu(-6)=2, Bu(7)= Bu(-7)=1, Bu(8)= Bu(-8)=0.
Рис. 2.6. АКФ функции Уолша 2-го порядка.
Функция Уолша 7-го порядка
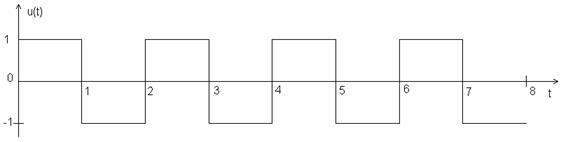
Bu(0)=8, Bu(1)= Bu(-1)=-7, Bu(2)= Bu(-2)=6, Bu(3)= Bu(-3)=-5, Bu(4)= Bu(-4)=4, Bu(5)= Bu(-5)=-3, Bu(6)= Bu(-6)=2, Bu(7)= Bu(-7)=-1, Bu(8)= Bu(-8)=0.
Рис. 2.7. АКФ функции Уолша 7-го порядка.
Типы сложных сигналов
Сигнал – это физический процесс, который может нести полезную информацию и распространяться по линии связи. Под сигналом s(t) будем понимать функцию времени, отображающую физический процесс, имеющий конечную длительность Т.
|
|
|
Сигналы, у которых база В, равная произведению длительности сигнала Т на ширину его спектра, близка к единице, называются «простыми» или «обыкновенными». Различение таких сигналов может быть осуществлено по частоте, времени (задержке) и фазе.
Сложные, многомерные, шумоподобные сигналы формируются по сложному закону. За время длительности сигнала Т он подвергается дополнительной манипуляции (или модуляции) по частоте или фазе. Дополнительная модуляция по амплитуде используется редко. За счет дополнительной модуляции спектр сигнала Δf (при сохранении его длительности Т) расширяется. Следовательно, для такого сигнала B=T Δf>>1.
При некоторых законах формирования сложного сигнала его спектр оказывается сплошным и практически равномерным, т.е. близким к спектру шума с ограниченной шириной полосы. При этом функция автокорреляции сигнала имеет один основной выброс, ширина которого определяется не длительностью сигнала, а шириной его спектра, т.е. имеет вид, аналогичный функции автокорреляции шума с ограниченной полосой частот. В связи с этим такие сложные сигналы называют шумоподобными. [5]
Шумоподобные сигналы получили применение в широкополосных системах связи, так как: обеспечивают высокую помехозащищенность систем связи; позволяют организовать одновременную работу многих абонентов в общей полосе частот; позволяют успешно бороться с многолучевым распространением радиоволн путем разделения лучей; обеспечивают лучшее использование спектра частот на ограниченной территории по сравнению с узкополосными системами связи.
Известно большое число различных шумоподобных сигналов (ШПС). Тем не менее, выделяют следующие основные ШПС: частотно-модулированные сигналы; многочастотные сигналы; фазоманипулированные сигналы; дискретные частотные сигналы; дискретные составные частотные сигналы.
Частотно-модулированные сигналы (ЧМ) являются непрерывными сигналами, частота которых меняется по заданному закону (рис. 2.8.).
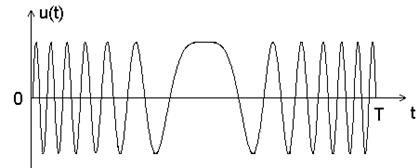
Рис. 2.8. ЧМ сигнал.
В системах связи необходимо иметь множество сигналов. При этом необходимость быстрой смены сигналов и переключения аппаратуры формирования и обработки приводят к тому, что закон изменения частоты становится дискретным. При этом от ЧМ сигналов переходят к ДЧ сигналам.
|
|
|
Многочастотные (МЧ) сигналы являются суммой N гармоник u1(t)…uN(t), амплитуды и фазы которых определяются в соответствии с законами формирования сигналов (рис. 2.9.).
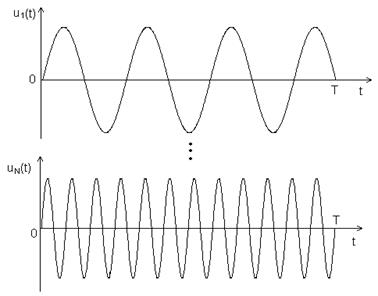
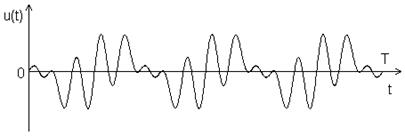
Рис. 2.9. МЧ сигнал.
МЧ сигналы являются непрерывными и для их формирования и обработки трудно приспособить методы цифровой техники.
Фазоманипулированные (ФМ) сигналы представляют последовательность радиоимпульсов, фазы которых изменяются по заданному закону (рис. 2.10., а). Обычно фаза принимает два значения (0 или π). При этом радиочастотному ФМ сигналу соответствует видео-ФМ сигнал (рис. 2.10., б).
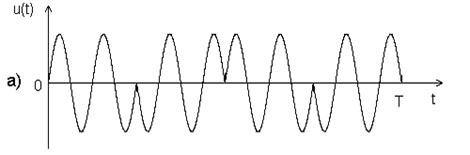
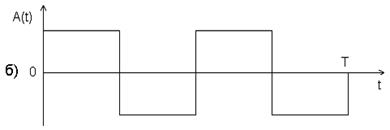
Рис. 2.10. ФМ сигнал.
ФМ сигналы весьма распространены, т.к. они позволяют широко использовать цифровые методы при формировании и обработке, и можно реализовать такие сигналы с относительно большими базами.
Дискретные частотные (ДЧ) сигналы представляют последовательность радиоимпульсов (рис. 2.11.), несущие частоты которых изменяются по заданному закону.
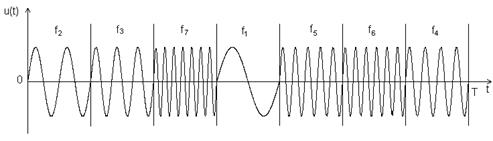
Рис. 2.11. ДЧ сигнал.
Дискретные составные частотные (ДСЧ) сигналы являются ДЧ сигналами, у которых каждый импульс заменен шумоподобным сигналом.
На рис. 2.12. изображен видеочастотный ФМ сигнал, отдельные части которого передаются на различных несущих частотах. [6]
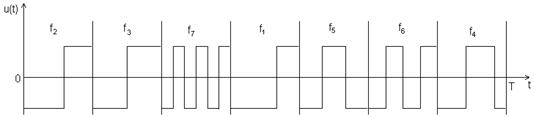
Рис. 2.12. ДСЧ сигнал.
|
|
|
