 |
Квадратурная модуляция и ее характеристики ( Q PSK , QAM )
|
|
|
|
Рассмотрим квадратурную фазовую манипуляцию (QPSK). Исходный поток данных dk(t)=d0, d1, d2,… состоит из биполярных импульсов, т.е. dk принимают значения +1 или -1 (рис. 3.5.а)), представляющие двоичную единицу и двоичный нуль. Этот поток импульсов разделяется на синфазный поток dI(t) и квадратурный - dQ(t), как показано на рис. 3.5.б).
dI(t)=d0, d2, d4,… (четные биты)
dQ(t)=d1, d3, d5,… (нечетные биты)
Удобную ортогональную реализацию сигнала QPSK можно получить, используя амплитудную модуляцию синфазного и квадратурного потоков на синусной и косинусной функциях несущей.

С помощью тригонометрических тождеств s(t) можно представить в следующем виде: s(t)=cos(2πf0t+θ(t)). Модулятор QPSK, показанный на рис. 3.5.в), использует сумму синусоидального и косинусоидального слагаемых. Поток импульсов dI(t) используется для амплитудной модуляции (с амплитудой +1 или -1) косинусоиды. Это равноценно сдвигу фазы косинусоиды на 0 или π; следовательно, в результате получаем сигнал BPSK. Аналогично поток импульсов dQ(t) модулирует синусоиду, что дает сигнал BPSK, ортогональный предыдущему. При суммировании этих двух ортогональных компонентов несущей получается сигнал QPSK. Величина θ(t) будет соответствовать одному из четырех возможных сочетаний dI(t) и dQ(t) в выражении для s(t): θ(t)=00, ±900 или 1800; результирующие векторы сигналов показаны в сигнальном пространстве на рис. 3.6. Так как cos(2πf0t) и sin(2πf0t) ортогональны, два сигнала BPSK можно обнаруживать раздельно. QPSK обладает рядом преимуществ перед BPSK: т.к. при модуляции QPSK один импульс передает два бита, то в два раза повышается скорость передачи данных или при той же скорости передачи данных, что и в схеме BPSK, используется в два раза меньшая полоса частот; а так же повышается помехоустойчивость, т.к. импульсы в два раза длиннее, а следовательно и больше по мощности, чем импульсы BPSK. [2]
|
|
|
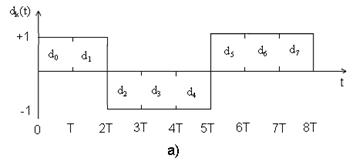
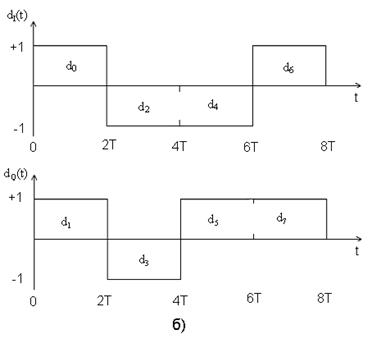

Рис. 3.5. Модуляция QPSK.
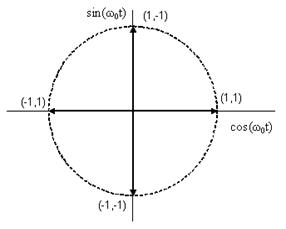
Рис. 3.6. Сигнальное пространство для схемы QPSK.
Квадратурную амплитудную модуляцию (KAM, QAM) можно считать логическим продолжением QPSK, поскольку сигнал QAM также состоит из двух независимых амплитудно-модулированных несущих.
При квадратурной амплитудной модуляции изменяется как фаза, так и амплитуда сигнала, что позволяет увеличить количество кодируемых бит и при этом существенно повысить помехоустойчивость. Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих – синусоидальной и косинусоидальной (синфазной и квадратурной):
s(t)=A(t)cos(ωt + φ(t))=x(t)sinωt + y(t)cosωt, где
x(t)=A(t)(-sinφ(t)),y(t)=A(t)cosφ(t)
Такая дискретная модуляция (манипуляция) осуществляется по двум каналам, на несущих, сдвинутых на 900 друг относительно друга, т.е. находящихся в квадратуре (отсюда и название).
Поясним работу квадратурной схемы на примере формирования сигналов четырехфазной ФМ (ФМ-4) (рис. 3.7).
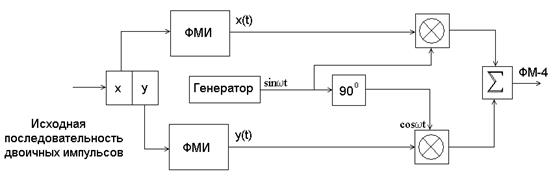
Рис. 3.7. Схема квадратурного модулятора.
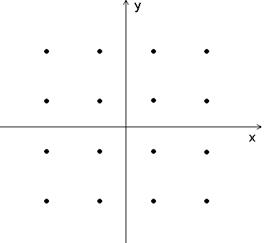
Рис. 3.8. 16-ричное пространство сигналов (QAM-16).
Исходная последовательность двоичных символов длительностью Т при помощи регистра сдвига разделяется на нечетные импульсы y, которые подаются в квадратурный канал (cosωt), и четные – x, поступающие в синфазный канал (sinωt). Обе последовательности импульсов поступают на входы соответствующих формирователей манипулированных импульсов, на выходах которых образуются последовательности биполярных импульсов x(t) и y(t) с амплитудой ±Um и длительностью 2T. Импульсы x(t) и y(t) поступают на входы канальных перемножителей, на выходах которых формируются двухфазные (0, π) ФМ колебания. После суммирования они образуют сигнал ФМ-4.
|
|
|
На рис. 3.8. показано двухмерное пространство сигналов и набор векторов сигналов, модулированных 16-ричной QAM и изображенных точками, которые расположены в виде прямоугольной совокупности.
Из рис. 3.8. видно, что расстояние между векторами сигналов в сигнальном пространстве при QAM больше, чем при QPSK, следовательно, QAM является более помехоустойчивой по сравнению с QPSK,
|
|
|


