 |
Меры центральной тенденции и меры изменчивости
|
|
|
|
Задание:
При проведении исследования особенностей внимания были получены следующие результаты (в баллах):
| 1; 2: 3; 4; 5; 6; 7; 8; 9; 8; 7; 6; 5; 6; 7; 8; 7; 6; 5; 4; 3; 2; 1; 2; 3; 4; 5; 4; 3; 2; 1; 2; 3; 4; 5; 6; 7; 8; 9; 8; 7; 7; 6; 5; 4; 5; 1; 2; 3; 4; 5; 6; 7; 8; 9; 8; 7; 6; 5; 4; 3; 2; 3; 4; 5; 6; 7; 8; 7; 6; 5; 4; 3; 4; 6; 6; 7; 6; 5; 4; 5; 6; 7; 6; 5; 4; 3; 4; 5; 6; 7; 6; 5; 4; 3; 4; 5; 6; 7; 6 |
Посчитать среднее арифметическое полученных результатов, определить моду, медиану, посчитать размах данных, дисперсию, стандартное отклонение.
Решение:
Представим данные в табличной форме.
Расчеты также будем проводить в таблице. Это позволяет упростить процедуру подсчета.
| Значения (A) | f | f *А | Хi-М | (Хi-М)² | f*(Хi-М)² |
| -4,1 | 16,81 | 67,24 | |||
| -3,1 | 9,61 | 67,27 | |||
| -2,1 | 4,41 | 48,51 | |||
| -1,1 | 1,21 | 19,36 | |||
| -0,1 | 0,01 | 0,17 | |||
| 0,9 | 0,81 | 15,39 | |||
| 1,9 | 3,61 | 54,15 | |||
| 2,9 | 8,41 | 67,28 | |||
| 3,9 | 15,21 | 45,63 | |||
| СУММА |
Крайние значения: Min=1, Max=9
Размах: R=9-1=8
Среднее арифметическое: М=510/100=5,1
Мода: Мо=6
Медиана: Ме=5
Дисперсия: S²=385/99 ≈ 3,89
Стандартное отклонение: σ ≈ 1,97
ДОМАШНЕЕ ЗАДАНИЕ:
При проведении исследования индивидуальных особенностей мышления были получены следующие результаты (в баллах):
| 5; 2: 2; 4; 5; 7; 7; 8; 9; 8; 1; 6; 5; 6; 3; 8; 7; 1; 5; 4; 3; 8; 5; 2; 3; 9; 5; 4; 3; 4; 1; 7; 3; 4; 5; 6; 7; 3; 9; 8; 7; 7; 6; 1; 4; 5; 1; 2; 3; 4; 5; 6; 7; 8; 9; 8; 7; 6; 5; 4; 3; 7; 3; 4; 5; 6; 7; 2; 7; 6; 5; 4; 3; 9; 6; 2; 4; 6; 5; 6; 5; 6; 7; 6; 5; 4; 3; 4; 5; 6; 7; 6; 5; 4; 3; 8; 5; 9; 7; 6 |
Посчитать среднее арифметическое полученных результатов, определить моду, медиану, посчитать размах данных, дисперсию, стандартное отклонение.
Практическое занятие 3
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
Задание:
Проверить, является ли полученное распределение нормальным. Данные (в баллах):
|
|
|
2; 4; 6; 5; 3; 4; 5; 6; 7; 8; 7; 6; 5; 4; 3; 2; 3; 4; 5; 6; 7; 8; 7; 6; 2; 3; 4; 5; 6; 7; 8; 9; 8; 7; 6; 5; 4; 3; 4; 7; 6; 5; 4; 1; 6; 5; 4; 1; 9; 7; 6; 5; 3; 4; 5; 4; 4; 5; 3; 4; 5; 6; 5; 6; 5; 4; 3; 4; 5; 6; 7; 6; 5; 4; 5; 6; 7; 6; 5; 4; 5; 6; 3; 6; 5; 1; 7; 6; 5; 4; 2; 3; 3; 4; 5; 6; 7; 2; 1; 3.
Решение:
Проводить расчеты удобнее с помощью таблицы.
| Значения (А) | f | f *А |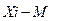 
| 
| f*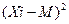 
|
| -3,9 | 15,21 | 60,84 | |||
| -2,9 | 8,41 | 42,05 | |||
| -1,9 | 3,61 | 43,32 | |||
| -0,9 | 0,81 | 15,39 | |||
| 0,1 | 0,01 | 0,22 | |||
| 1,1 | 1,21 | 24,2 | |||
| 2,1 | 4,41 | 52,92 | |||
| 3,1 | 9,61 | 38,44 | |||
| 4,1 | 16,81 | 33,62 | |||
| СУММА |
| Значения (А) | f |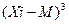 
| f*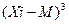
| 
| f*
|
| -59,319 | -237,276 | 231,3441 | 925,3764 | ||
| -24,389 | -121,945 | 70,7281 | 353,6405 | ||
| -6,859 | -82,308 | 13,0321 | 156,3852 | ||
| -0,729 | -13,851 | 0,6561 | 12,4659 | ||
| 0,001 | 0,022 | 0,0001 | 0,0022 | ||
| 1,331 | 26,62 | 1,4641 | 29,282 | ||
| 9,261 | 111,132 | 19,4481 | 233,3772 | ||
| 29,791 | 119,164 | 92,3521 | 369,4084 | ||
| 68,921 | 137,842 | 282,5761 | 565,1522 | ||
| СУММА | -60,6 | 2645,09 |
Для полученных данных:
М=490/100=4,9
σ ≈ 1,77
При подсчете асимметрии и эксцесса будем пользоваться упрощенными формулами.
σ³ ≈ 5,55
А = -60,6 / 555 ≈ -0,11
σ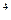 
≈ 9,82
Е = (2645,09 / 982)-3 ≈ -0,31
Итак, мы получили распределение, которое характеризуется средним значением 4,9±1,77 и незначительной асимметрией (-0,11), небольшим отрицательным эксцессом (-0,31).
Проверяем нормальность распределения по методу Н.А. Плохинского
mA ≈ 0,24
mЕ ≈ 0,48
tА= 0,11 / 0,24 ≈ 0,46
tЕ= 0,31 / 0,48 ≈ 0,65
tА < 3 и tЕ < 3, значит, распределение является нормальным.
Проверяем нормальность распределения по методу Е.И.Пустыльник
Акр. ≈ 0,72
Екр. ≈ 2,27
А < Акр. и Е < Екр., значит, распределение является нормальным.
ДОМАШНЕЕ ЗАДАНИЕ:
Проверить, является ли следующее распределение нормальным. Применять для проверки 2 способа (по Н.А.Плохинскому и Е.И.Пустыльник)
7; 4; 5; 2; 3; 1; 8; 4; 2; 8; 5; 4; 7; 6; 8; 7; 3; 6; 8; 6; 5; 3; 9; 1; 4; 7; 3; 2; 7; 7; 6; 3; 1; 4; 8; 2; 5; 8; 7; 3; 6; 5; 6; 7; 1; 2; 3; 4; 5; 6; 7; 9; 6; 8; 6; 5; 4; 7; 6; 7; 4; 2; 5; 8; 6; 4; 5; 7; 1; 7; 4; 6; 5; 7; 4; 7; 3; 6; 8; 5; 9; 5; 7; 4; 5; 7; 9; 8; 7; 6; 5; 3; 1; 5; 3; 7; 6; 3; 8; 1.
|
|
|
Практическое занятие 4
СТАНДАРТИЗАЦИЯ
1 Задание:
Стандартизирующая выборка при проведении исследования особенностей памяти состояла из 100 человек. Диапазон возможных значений – от 0 до 50 баллов. При начальном анализе полученных результатов выяснили, что полученное распределение является нормальным, а среднее значение данных таково: 27,5±4,6.
Построить шкалу стенов.
Решение:
Начнем решение задачи с графического представления шкалы стенов.
стены 1 2 3 4 5 6 7 8 9 10
 |
границы М-2σ М-1,5σ М-σ М-0,5σ М М+0,5σ М+σ М+1,5σ М+2σ
для данной
выборки: 18,3 20,6 22,9 25,2 27,5 29,8 32,1 34,4 36,7
Подсчитав границы между стенами, можно указать диапазон значений в каждом стене.
| стены | диапазон значений (баллы) |
| 0-18 | |
| 19-20 | |
| 21-22 | |
| 23-25 | |
| 26-27 | |
| 28-29 | |
| 30-32 | |
| 33-34 | |
| 35-36 | |
| 37-50 |
2 Задание:
Проводится стандартизация методики. Возможный диапазон значений – от 10 до 50 баллов. При начальном анализе полученных результатов выяснили, что распределение данных является нормальным, а среднее значение равно 32,5±3,6. Построить 2 варианта z-шкалы: для 5 и 7 групп.
Решение:
Строим сначала z-шкалу для 5 групп.
г руппы 1 2 3 4 5
 |
границы М-2σ М-σ М+σ М+2σ
Для данной
выборки: 25,3 28,9 36,1 39,7
Определив границы, можно представить итоговую информацию в таблице:
| Группы | диапазон значений (баллы) | уровни |
| 10-25 | низкий | |
| 26-28 | ниже среднего | |
| 29-36 | средний | |
| 37-39 | выше среднего | |
| 40-50 | высокий |
Строим z-шкалу для 7 групп.
группы 1 2 3 4 5 6 7
 |
границы М-2σ М-(4/3σ) М-(2/3σ) М+(2/3σ) М+(4/3σ) М+2σ
Для данной
выборки: 25,3 27,7 30,1 34,9 37,3 39,7
Строим таблицу для перевода «сырых» баллов в z-показатель:
| Группы | диапазон значений (баллы) | уровни |
| 10-25 | очень низкий | |
| 26-27 | низкий | |
| 28-30 | ниже среднего | |
| 31-34 | средний | |
| 35-37 | выше среднего | |
| 38-39 | высокий | |
| 40-50 | очень высокий |
ДОМАШНЕЕ ЗАДАНИЕ:
Проводится стандартизация методики. Диапазон возможных значений –от 0 до 100 баллов. При начальном анализе полученных результатов выяснили, что полученное распределение является нормальным, а среднее значение данных таково: 46,3±13,8.
|
|
|
Построить шкалу стенов и 2 варианта z-шкалы: для 5 и 7 групп.
3 задание:
При проведении стандартизации исследовали 200 человек. Возможный диапазон значений от 0 до 12 баллов. Полученные данные сгруппированы в таблицу.
| балл | |||||||||||||
| количество человек, набравших этот балл |
Провести процентильную нормализацию, в частности, построить пятибалльную шкалу.
Решение:
Первая группа в пятибалльной шкале должна составлять 7% от всех испытуемых, в нашем случае -14 человек. Границей, отделяющей первых 14 человек от остальных, являются баллы от 0 до 3 включительно. Вторая группа должна составлять 24%, в нашем случае 48 человек. Левая граница второй границы – 4 балла, на правой границе суммарное число испытуемых должно составлять 48, т.е. правой границей будет 6 балл. Третья группа включает 38%, в нашем случае 76 человек, левая граница -7 баллов, правая – 8. Четвертая группа включает 24%, значит, 48 человек. Левая ее граница -9 баллов, правая -10. Пятая группа -7%, в нашем случае 14 человек. Левая граница пятой группы -11 баллов, правая – 12. Полученные данные представим в табличной форме.
| Группы | диапазон значений (баллы) | уровни |
| 0-3 | низкий | |
| 4-6 | ниже среднего | |
| 7-8 | средний | |
| 9-10 | выше среднего | |
| 11-12 | высокий |
ДОМАШНЕЕ ЗАДАНИЕ:
В проведении стандартизации методики принимали участие 100 человек. Возможный диапазон значений от 0 до 13 баллов. Полученные данные сгруппированы в таблицу.
| балл | ||||||||||||||
| количество человек, набравших этот балл |
Провести процентильную нормализацию, в частности, построить семибалльную шкалу.
Практическое занятие 5
|
|
|
