 |
Выявление различий в распределении признака
|
|
|
|
1 задание:
Проводилось изучение предпочитаемого цвета. Испытуемым предлагалось выбрать один из 5 цветов: белый, синий, красный, желтый, зеленый. Затем подсчитали количество выборов, пришедшихся на каждый цвет, и эти результаты занесли в таблицу:
| цвет | белый | синий | красный | желтый | зеленый |
| кол-во выборов |
Можно ли достоверно утверждать, что все цвета предпочтительны в равной мере?
Решение:
Для решения задачи нам необходимо сопоставить полученное эмпирическое распределение с теоретическим равномерным.
Формулируем статистические гипотезы:
Н0: распределение предпочтений цвета значимо не отличается от равномерного распределения
Н1: распределение предпочтений цвета значимо отличается от равномерного распределения
Проводить расчеты удобнее с помощью таблицы.
| цвет | fэмп | f теор | fэмп - fтеор | (fэмп - f теор)² | (fэмп-f теор)² / fтеор |
| белый | -6 | ||||
| синий | -4 | 1,33 | |||
| красный | 2,08 | ||||
| желтый | 0,33 | ||||
| зеленый | 0,75 | ||||
| сумма | 7,49 |
fтеор=60/5=12
χ²эмп=7,49
Определяем критические значения χ²-критерия по таблице 2 при df=5-1=4
χ² кр= 7,779 при р≤0,1
χ² кр= 9,488 при р≤0,05
χ² кр= 13,278 при р≤0,01
χ² эмп< χ² кр, принимается Н0 т.е. не обнаружены статистически достоверные различия между распределением предпочтения цвета и равномерным распределением.
ДОМАШНЕЕ ЗАДАНИЕ:
Проводилось исследование предпочтений при выборе стиля поведения в конфликте. Испытуемым предлагалось выбрать один из 5 стилей: компромисс, уступка, избегание, сотрудничество, соперничество. Затем подсчитали количество выборов, пришедшихся на каждый стиль, и эти результаты занесли в таблицу:
|
|
|
| стиль | компромисс | уступка | избегание | сотрудничество | соперничество |
| кол-во выборов |
Можно ли достоверно утверждать, что все стили поведения предпочтительны в равной мере?
2 задание:
При заучивании двузначных чисел в двух группах испытуемых были получены следующие результаты:
| объем воспроизведения | |||||
| кол-во испытуемых из 1 группы | |||||
| кол-во испытуемых из 2 группы |
Значимо ли различие частот в этих двух группах?
Решение:
Формулируем статистические гипотезы:
Н0: два эмпирических распределения значимо не отличаются друг от друга
Н1: два эмпирических распределения значимо отличаются друг от друга
Проводить расчеты будем по упрощенной формуле, без определения теоретической частоты.
| объем воспроизв. | f1 | f 2 | f1 – f2 | (f1- f 2)² | f1+f2 | (f1- f 2)²/ (f1+f2) |
| 0,11 | ||||||
| 2,33 | ||||||
| 0,22 | ||||||
| -5 | 1,67 | |||||
| -5 | 3,57 | |||||
| сумма | 7,9 |
χ²эмп=7,9
Определяем критические значения χ²-критерия по таблице 2 при df=5-1=4
χ² кр= 7,779 при р≤0,1; χ² кр= 9,488 при р≤0,05
χ² кр= 13,278 при р≤0,01
χ² эмп> χ² кр (р≤0,1), принимается Н1, т.е. обнаружены различия на уровне тенденции (р≤0,1) между двумя группами в эффективности воспроизведения двузначных чисел.
ДОМАШНЕЕ ЗАДАНИЕ:
При изучении эффективности запоминания слов в двух группах испытуемых были получены следующие результаты:
| объем воспроизведения | |||||||
| кол-во испытуемых из 1 группы | |||||||
| кол-во испытуемых из 2 группы |
Значимо ли различие частот в этих двух группах? При решении задачи пользоваться упрощенной формулой (без подсчета теоретической частоты).
|
|
|
3 задание:
При проведении исследования мотивации на успех у мужчин и женщин были получены следующие результаты:
| показатель мотивации | 0-10 | 11-20 | 21-30 | 31-40 |
| мужчины | ||||
| женщины |
Значимо ли различие частот в этих двух группах?
Решение:
Формулируем статистические гипотезы:
Н0: два эмпирических распределения значимо не отличаются друг от друга
Н1: два эмпирических распределения значимо отличаются друг от друга
Считаем суммы частот по строкам и столбцам:
| показатель мотивации | 0-10 | 11-20 | 21-30 | 31-40 | сумма |
| мужчины | |||||
| женщины | |||||
| сумма |
Дальнейшие расчеты будем производить в таблице:
| гр. | fэмп | fтеор | fэмп – fтеор | (fэмп - f теор)² | (fэмп-f теор)² / fтеор | |
| м у ж ч | 20*60/100 | -4 | 1,33 | |||
| 29*60/100 | 17,4 | -3,4 | 11,6 | 0,67 | ||
| 30*60/100 | 0,22 | |||||
| 21*60/100 | 12,6 | 5,4 | 29,2 | 2,32 | ||
| ж е н щ | 20*40/100 | |||||
| 29*40/100 | 11,6 | 3,4 | 11,6 | |||
| 30*40/100 | -2 | 0,33 | ||||
| 21*40/100 | 8,4 | -5,4 | 29,2 | 3,48 | ||
| 11,35 |
χ²эмп=11,35
df=(2-1)*(4-1)=4
Определяем критические значения χ²-критерия по таблице 2 при df=4
χ² кр= 7,779 при р≤0,1
χ² кр= 9,488 при р≤0,05
χ² кр= 13,278 при р≤0,01
χ² эмп> χ² кр (р≤0,05), принимается Н1, т.е. обнаружены достоверные различия (р≤0,05) между мужчинами и женщинами в проявлении мотивации на успех.
ДОМАШНЕЕ ЗАДАНИЕ:
При проведении исследования эмпатии у мужчин и женщин были получены следующие результаты:
| показатель эмпатии | 0-10 | 11-20 | 21-30 | 31-40 | 41-50 |
| мужчины | |||||
| женщины |
Значимо ли различие частот в этих двух группах?
4 задание:
При проведении исследования с целью изучения связи между сменой профиля обучения и успешностью обучения у школьников 7 класса были получены следующие результаты (в таблице указано количество человек, имеющих соответствующие характеристики):
| профиль обучения менялся | профиль обучения не менялся | |
| повышение эффективности обучение | ||
| снижение эффективности обучение |
Определить, существует ли статистически достоверная связь между сменой профиля обучения и успешностью обучения. При решении задачи использовать φ-критерий.
|
|
|
Решение:
Формулируем статистические гипотезы:
Н0: связь между сменой профиля обучения и успешностью обучения является случайной
Н1: связь между сменой профиля обучения и успешностью обучения не является случайной
φ= 
≈ 0,65
χ²=63*0,65² ≈ 26,6
Определяем критические значения χ²-критерия по таблице 2 при df=1
χ² кр= 2,706 при р≤0,1; χ² кр= 3,842 при р≤0,05; χ² кр= 6,635 при р≤0,01
χ² эмп> χ² кр (р≤0,01), принимается Н1, т.е. установлена высокозначимая статистическая связь между сменой профиля обучения и успешностью обучения
ДОМАШНЕЕ ЗАДАНИЕ:
Валидность методики часто определяют при помощи сравнения результатов теста с мнением группы экспертов. В таблицу внесены полученные результаты (количество человек, имеющих соответствующие показатели).
| результаты теста | результаты экспертной проверки | |
| высокий уровень | низкий уровень | |
| высокий уровень | ||
| низкий уровень |
Является ли данная методика валидной? (Используйте φ-критерий. Затем по степени связи между результатами теста и экспертной проверки делают вывод о валидности).
Практическое занятие 8
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
1 задание:
Применение методики Рокича (в частности, использовался список терминальных ценностей) для двух позиций (Я-реальное и Я-идеальное) у испытуемого А. дало следующие результаты (см.2 и 3 столбец):
| испытуемый А. | испытуемый Б. | |||
| позиция ценность | Я-реальное | Я-идеальное | Я-реальное | Я-идеальное |
| ранг | ранг | |||
| активная жизнь | ||||
| жизненная мудрость | ||||
| здоровье | ||||
| интересная работа | ||||
| красота природы | ||||
| любовь | ||||
| материальное обеспеч. | ||||
| друзья | ||||
| обществ.признание | ||||
| познание | ||||
| продуктивная жизнь | ||||
| развитие | ||||
| развлечения | ||||
| свобода | ||||
| семейная жизнь | ||||
| счастье других | ||||
| творчество | ||||
| уверенность в себе |
Вычислить коэффициент ранговой корреляции Спирмена между позициями Я-реальное и Я-идеальное для данных испытуемого А., определить силу и значимость корреляционной связи.
|
|
|
Решение:
Формулируем статистические гипотезы:
Н0: корреляция между позицией Я-реальное и позицией Я-идеальное значимо не отличается от нуля (является случайной).
Н1: корреляция между позицией Я-реальное и позицией Я-идеальное значимо отличается от нуля (является неслучайной).
Расчеты удобнее вести в таблице.
| позиция ценность | Я-реальное | Я-идеальное | ||
| ранг | d | d² | ||
| активная жизнь | ||||
| жизненная мудрость | -5 | |||
| здоровье | ||||
| интересная работа | -2 | |||
| красота природы | ||||
| любовь | -1 | |||
| материальное обеспеч. | -1 | |||
| друзья | ||||
| обществ.признание | ||||
| познание | -2 | |||
| продуктивная жизнь | -5 | |||
| развитие | -1 | |||
| развлечения | ||||
| свобода | ||||
| семейная жизнь | ||||
| счастье других | -1 | |||
| творчество | ||||
| уверенность в себе | -2 | |||
| сумма |
rs = 1 - 
rs = 1 – (6*156)/(18*323) = 1 – 936/5814 ≈ 1-0,16 = 0,84
0,84>0 и 0,84>0,7
Т.е., корреляционная связь положительная и сильная.
Определяем критические значения rs по таблице 5 при п =18
rs кр= 0,400 при р≤0,1
rs кр= 0,468 при р≤0,05
rs кр= 0,590 при р≤0,01
rs кр= 0,708 при р≤0,001
rs эмп> rs кр (р≤0,001), то есть полностью характеризуем корреляционную связь: положительная, сильная, высокозначимая.
Итак, принимается Н1, т.е. обнаружена сильная и высокозначимая корреляционная связь между позициями Я-реальное и Я-идеальное у испытуемого А.
ДОМАШНЕЕ ЗАДАНИЕ:
Определить характер корреляционной связи между позициями Я-реальное и Я-идеальное у испытуемого Б. (см. 4 и 5 столбец таблицы задания 1) с помощью коэффициента корреляции Спирмена.
2 задание:
Применение методики Рокича (в частности, использовался список терминальных ценностей) для двух позиций: Я-реальное и Я-идеальное у испытуемого В. дало следующие результаты (см.2 и 3 столбец):
| испытуемый В. | испытуемый Г. | |||
| позиция ценность | Я-реальное | Я-идеальное | Я-реальное | Я-идеальное |
| ранг | ранг | |||
| активная жизнь | ||||
| жизненная мудрость | ||||
| здоровье | ||||
| интересная работа | ||||
| красота природы | ||||
| любовь | ||||
| материальное обеспеч. | ||||
| друзья | ||||
| обществ.признание | ||||
| познание | ||||
| продуктивная жизнь | ||||
| развитие | ||||
| развлечения | ||||
| свобода | ||||
| семейная жизнь | ||||
| счастье других | ||||
| творчество | ||||
| уверенность в себе |
Вычислить коэффициент ранговой корреляции Спирмена между позициями Я-реальное и Я-идеальное для данных испытуемого В., определить силу и значимость корреляционной связи.
|
|
|
Решение:
Формулируем статистические гипотезы:
Н0: корреляция между позицией Я-реальное и позицией Я-идеальное значимо не отличается от нуля (является случайной).
Н1: корреляция между позицией Я-реальное и позицией Я-идеальное значимо отличается от нуля (является неслучайной).
Расчеты удобнее вести в таблице.
| Я-реальное | Я-идеальное | d | d² | |||
| ценность | ранг ст. | ранг н. | ранг ст. | ранг н. | ||
| активная жизнь | 9,5 | 6,5 | ||||
| жизненная мудрость | 1,5 | 11,5 | 132,25 | |||
| здоровье | 1,5 | 0,5 | 0,25 | |||
| интересная работа | ||||||
| красота природы | ||||||
| любовь | 6,5 | -2,5 | 6,25 | |||
| материальное обеспеч. | ||||||
| друзья | -3 | |||||
| обществ.признание | -1 | |||||
| познание | ||||||
| продуктивная жизнь | 9,5 | -6,5 | 42,25 | |||
| развитие | 5,5 | 3,5 | ||||
| развлечения | -4 | |||||
| свобода | -7 | |||||
| семейная жизнь | 3,5 | 3,5 | 12,25 | |||
| счастье других | -3 | |||||
| творчество | -3 | |||||
| уверенность в себе | 5,5 | -8,5 | 72,25 | |||
| сумма | 487,5 |
Проверим правильность проведения ранжирования:
Расчетная сумма=18*19/2=171
Сумма «новых» рангов в обеих позициях равна 171, т.е. ранжирование проведено верно.
rs = 1 - 
-формула с поправками на связные ранги
Та= [(3³-3)+(2³-2)+(2³-2)]/12=[24+6+6]/12=3
Тв= [(2³-2)+(2³-2)+(2³-2)]/12=[6+6+6]/12=1,5
rs = 1 – (6*487,5+3+1,5)/(18*323) = 1 – 2929,5/5814 ≈ 1-0,5 = 0,5
0,5>0 и 0,5=0,5
Т.е., корреляционная связь положительная и средняя по силе.
Определяем критические значения rs по таблице при п =18
rs кр= 0,400 при р≤0,1
rs кр= 0,468 при р≤0,05
rs кр= 0,590 при р≤0,01
rs эмп> rs кр (р≤0,05), то есть полностью характеризуем корреляционную связь: положительная, средняя по силе и значимая корреляция.
Итак, принимается Н1, т.е. обнаружена положительная, средняя и значимая (р≤0,05) корреляционная связь между позициями Я-реальное и Я-идеальное у испытуемого В.
ДОМАШНЕЕ ЗАДАНИЕ:
Определить характер корреляционной связи между позициями Я-реальное и Я-идеальное у испытуемого Г. (см. 4 и 5 столбец таблицы задания 2) при помощи коэффициента корреляции Спирмена.
3 задание:
Десять испытуемых (А, Б, В и т.д.) в экспериментах по запоминанию двузначных чисел и запоминанию слов имели следующие результаты (в баллах):
| испытуемый | А | Б | В | Г | Д | Е | Ж | З | И | К |
| запоминание чисел | ||||||||||
| запоминание слов |
Определить, используя коээфициент корреляции Пирсона, коррелируют ли между собой два показателя эффективности запоминания. При этом считать, что оба распределения являются нормальными.
Решение:
Формулируем статистические гипотезы:
Н0: корреляция между показателями значимо не отличается от нуля (является случайной).
Н1: корреляция между показателями значимо отличается от нуля (является неслучайной).
Показатели запоминания чисел будем обозначать как Х, показатели запоминания слов –Y.
Расчеты удобнее вести в таблице.
| испы- туемый | Xi | Yi | Х | Y | Х* Y | Х² | Y² |
| А | -0,8 | -1,3 | 1,04 | 0,64 | 1,69 | ||
| Б | 0,2 | 2,7 | 0,54 | 0,04 | 7,29 | ||
| В | 0,2 | 1,7 | 0,34 | 0,04 | 2,89 | ||
| Г | 1,2 | -0,3 | -0,36 | 1,44 | 0,09 | ||
| Д | -0,8 | -2,3 | 1,84 | 0,64 | 5,29 | ||
| Е | 0,2 | -1,3 | -0,26 | 0,04 | 1,69 | ||
| Ж | 1,2 | 1,7 | 2,04 | 1,44 | 2,89 | ||
| З | -1,8 | 0,7 | -1,26 | 3,24 | 0,49 | ||
| И | -0,8 | -1,3 | 1,04 | 0,64 | 1,69 | ||
| К | 1,2 | -0,3 | -0,36 | 1,44 | 0,09 | ||
| сумма | 4,6 | 9,6 | 24,1 |
Хср=38/10=3,8
Yср=63/10=6,3
X = Xi-Хср
Y = Yi -Yср
ρ = 
≈ 0,3
Определяем критические значения ρ по таблице при п =10
ρ кр= 0,549 при р≤0,1
ρ кр= 0,632 при р≤0,05
ρ кр= 0,765 при р≤0,01
ρ эмп< ρ кр,значит, принимается Н0, т.е. корреляция между показателями не является статистически значимой.
ДОМАШНЕЕ ЗАДАНИЕ:
Девять испытуемых (А, Б, В и т.д.) в экспериментах по запоминанию разнородных и однотипных фигур имели следующие результаты (в баллах):
| испытуемый | А | Б | В | Г | Д | Е | Ж | З | И |
| разнородные фигуры | |||||||||
| однотипные фигуры |
Определить, используя коэффициент корреляции Пирсона, существует ли значимая корреляционная связь между показателями. При этом считать, что оба распределения являются нормальными.
4 задание:
Дана корреляционная матрица (для подсчетов применялся коэффициент корреляции Пирсона). Нужно отметить в ней статистически значимые корреляции. Построить корреляционный граф.
| А | Б | В | Г | Д | Е | Ж | З | И | К | |
| А | ||||||||||
| Б | -0,62 | |||||||||
| В | 0,24 | -0,16 | ||||||||
| Г | -0,10 | 0,40 | -0,15 | |||||||
| Д | -0,27 | 0,43 | 0,08 | 0,36 | ||||||
| Е | -0,17 | 0,32 | 0,10 | 0,14 | 0,66 | |||||
| Ж | 0,08 | 0,14 | 0,01 | 0,45 | 0,01 | 0,44 | ||||
| З | 0,59 | -0,21 | 0,58 | -0,05 | -0,09 | 0,19 | -0,01 | |||
| И | -0,10 | -0,11 | 0,41 | -0,08 | -0,01 | -0,31 | -0,59 | 0,15 | ||
| К | 0,12 | -0,32 | -0,55 | -0,21 | -0,03 | 0,05 | 0,06 | -0,26 | -0,59 |
Решение:
Определяем критические значения ρ по таблице при п =10
ρ кр= 0,549 при р≤0,1 (*)
ρ кр= 0,632 при р≤0,05 (**)
ρ кр= 0,765 при р≤0,01 (***)
ρ кр= 0,872 при р≤0,001 (****)
| А | Б | В | Г | Д | Е | Ж | З | И | К | |
| А | ||||||||||
| Б | -0,62* | |||||||||
| В | 0,24 | -0,16 | ||||||||
| Г | -0,10 | 0,40 | -0,15 | |||||||
| Д | -0,27 | 0,43 | 0,08 | 0,36 | ||||||
| Е | -0,17 | 0,32 | 0,10 | 0,14 | 0,66** | |||||
| Ж | 0,08 | 0,14 | 0,01 | 0,45 | 0,01 | 0,44 | ||||
| З | 0,59* | -0,21 | 0,58* | -0,05 | -0,09 | 0,19 | -0,01 | |||
| И | -0,10 | -0,11 | 0,41 | -0,08 | -0,01 | -0,31 | -0,59* | 0,15 | ||
| К | 0,12 | -0,32 | -0,55* | -0,21 | -0,03 | 0,05 | 0,06 | -0,26 | -0,59* |
Строим корреляционный граф.
Типы линий, соединяющих
вершины корреляционного графа:
ρ> 0, р≤0,1
ρ< 0, р≤0,1
ρ> 0, р≤0,05
ДОМАШНЕЕ ЗАДАНИЕ:
Дана корреляционная матрица (для подсчетов применялся коэффициент корреляции Пирсона). Нужно отметить в ней статистически значимые корреляции. Построить корреляционный граф.
| А | Б | В | Г | Д | Е | Ж | З | И | К | |
| А | ||||||||||
| Б | 0,01 | |||||||||
| В | 0,18 | 0,50 | ||||||||
| Г | 0,21 | -0,16 | 0,51 | |||||||
| Д | -0,13 | -0,67 | -0,57 | 0,02 | ||||||
| Е | -0,28 | -0,24 | -0,37 | -0,22 | 0,29 | |||||
| Ж | 0,37 | -0,05 | 0,31 | 0,25 | -0,60 | 0,06 | ||||
| З | 0,36 | 0,17 | 0,71 | 0,37 | -0,35 | -0,79 | 0,12 | |||
| И | 0,55 | 0,11 | 0,12 | -0,28 | -0,38 | -0,61 | 0,21 | 0,62 | ||
| К | 0,44 | 0,16 | 0,13 | -0,21 | 0,01 | -0,33 | -0,03 | 0,39 | 0,61 |
Практическое занятие 9
РЕГРЕССИОННЫЙ АНАЛИЗ
1 задание:
Проводился эксперимент по выработке двигательного навыка. Записать уравнение регрессии для «независимой переменной» Х и «зависимой переменной» Y. В качестве переменной Х выступает номер пробы, Y- время выполнения задания (берется среднее арифметическое значение времени для группы испытуемых). Полученные результаты:
| № пробы | Хi | |||||||
| время (сек) | Yi | 16,0 | 14,5 | 13,5 | 12,5 | 12,5 | 12,0 | 11,0 |
Решение:
Поскольку у нас случай равноотстающих значений Х, то можно пользоваться упрощенным способом вычисления коэффициентов а и b в уравнении регрессии.
При этом ряд Х переводится в новое численное значение – ряд Х,начало отсчета которого приходится на середину ряда Х. Для единства обозначений формально будем писать Y вместо Y, хотя численно они не меняются.
| Хi | Xi | Yi | (Xi) ² | Xi * Yi |
| -3 | 16,0 | -48 | ||
| -2 | 14,5 | -29 | ||
| -1 | 13,5 | -13,5 | ||
| 12,5 | ||||
| 12,5 | 12,5 | |||
| 12,0 | ||||
| 11,0 | ||||
| сумма | -21 |
Xi = Хi – 4
a = -21/28 = - 0,75
b = 92/7 ≈ 13/1
Y=13,1 – 0,75 X = 13,1-0,75(Х-4)=13,1-0,75Х+3
Y=16,1 – 0,75Х –искомое уравнение регрессии
ДОМАШНЕЕ ЗАДАНИЕ:
Проводится исследование формирования навыка решения арифметических задач. Записать уравнение регрессии для «независимой переменной» Х и «зависимой переменной» Y. В качестве переменной Х выступает номер пробы, Y- количество верно выполненных заданий (берется среднее арифметическое значений для группы испытуемых). Полученные результаты:
| № пробы | Хi | |||||||
| кол-во заданий | Yi |
При решении задачи пользоваться упрощенным способом подсчета коэффициентов.
2 задание:
Проводилось исследование зависимости успешности в профессиональной деятельности от уровня коммуникативных навыков. Записать уравнение регрессии для «независимой переменной» Х и «зависимой переменной» Y. В качестве переменной Х выступает уровень коммуникативных навыков (изучался методом наблюдения, результаты даны в баллах), Y – успешность в профессиональной деятельности (изучалась методом экспертных оценок, результаты даны в баллах).
| испытуемый | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Х (ком.навыки) | ||||||||||
| Y (проф.успешн.) |
Решение:
Вычисления будем проводить в таблице:
| испы- туемый | Xi | Yi | Х | Y | Х* Y | Х² | Y² |
| А | -7 | -2 | |||||
| Б | -1 | -4 | |||||
| В | |||||||
| Г | -10 | -3 | |||||
| Д | |||||||
| Е | -5 | ||||||
| Ж | |||||||
| З | -2 | ||||||
| И | |||||||
| К | -4 | ||||||
| сумма |
Хср=310/10=31
Yср=60/10=6
X = Xi-Хср
Y = Yi -Yср
ρ =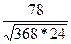 
≈ 0,83
σХ ≈ 6,4; σY ≈ 1,6
а =0,83*(1,6/6,4) ≈ 0,21
b =6-0,21*31= -0,51
Y= 0,21Х-0,51 - это искомое регрессионное уравнение зависимости успешности профессиональной деятельности от уровня коммуникативных навыков.
ДОМАШНЕЕ ЗАДАНИЕ:
Проводилось исследование зависимости успешности в профессиональной деятельности от мотивации на успех. Записать уравнение регрессии для «независимой переменной» Х и «зависимой переменной» Y. В качестве переменной Х выступает мотивация на успех (результаты даны в баллах), Y – успешность в профессиональной деятельности (результаты даны в баллах).
| испытуемый | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Х (мотив.успеха) | ||||||||||
| Y (проф.успешн.) |
ТАБЛИЦА 1 Критические значения t-критерия Стьюдента
| df | df | ||||||
| р≤0,1 | р≤0,05 | р≤0,01 | р≤0,1 | р≤0,05 | р≤0,01 | ||
| 6,314 | 12,70 | 63,65 | 1,678 | 2,012 | 2,685 | ||
| 2,920 | 4,303 | 9,925 | 1,677 | 2,011 | 2,682 | ||
| 2,353 | 3,182 | 5,841 | 1,677 | 2,010 | 2,680 | ||
| 2,132 | 2,776 | 4,604 | 1,676 | 2,009 | 2,678 | ||
| 2,015 | 2,571 | 4,032 | 1,675 | 2,008 | 2,676 | ||
| 1,943 | 2,447 | 3,707 | 1,675 | 2,007 | 2,674 | ||
| 1,895 | 2,365 | 3,499 | 1,674 | 2,006 | 2,672 | ||
| 1,860 | 2,306 | 3,355 | 1,674 | 2,005 | 2,670 | ||
| 1,833 | 2,262 | 3,250 | 1,673 | 2,004 | 2,668 | ||
| 1,812 | 2,228 | 3,169 | 1,673 | 2,003 | 2,667 | ||
| 1,796 | 2,201 | 3,106 | 1,672 | 2,002 | 2,665 | ||
| 1,782 | 2,179 | 3,055 | 1,672 | 2,002 | 2,663 | ||
| 1,771 | 2,160 | 3,012 | 1,671 | 2,001 | 2,662 | ||
| 1,761 | 2,145 | 2,977 | 1,671 | 2,000 | 2,660 | ||
| 1,753 | 2,131 | 2,947 | 1,670 | 2,000 | 2,659 | ||
| 1,746 | 2,120 | 2,921 | 1,670 | 1,999 | 2,657 | ||
| 1,740 | 2,110 | 2,898 | 1,669 | 1,998 | 2,656 | ||
| 1,734 | 2,101 | 2,878 | 1,669 | 1,998 | 2,655 | ||
| 1,729 | 2,093 | 2,861 | 1,669 | 1,997 | 2,654 | ||
| 1,725 | 2,086 | 2,845 | 1,668 | 1,997 | 2,652 | ||
| 1,721 | 2,080 | 2,831 | 1,668 | 1,996 | 2,651 | ||
| 1,717 | 2,074 | 2,819 | 1,668 | 1,995 | 2,650 | ||
| 1,714 | 2,069 | 2,807 | 1,667 | 1,995 | 2,649 | ||
| 1,711 | 2,064 | 2,797 | 1,667 | 1,994 | 2,648 | ||
| 1,708 | 2,060 | 2,787 | 1,667 | 1,994 | 2,647 | ||
| 1,706 | 2,056 | 2,779 | 1,666 | 1,993 | 2,646 | ||
| 1,703 | 2,052 | 2,771 | 1,666 | 1,993 | 2,645 | ||
| 1,701 | 2,049 | 2,763 | 1,666 | 1,993 | 2,644 | ||
| 1,699 | 2,045 | 2,756 | 1,665 | 1,992 | 2,643 | ||
| 1,697 | 2,042 | 2,750 | 1,665 | 1,992 | 2,642 | ||
| 1,696 | 2,040 | 2,744 | 1,665 | 1,991 | 2,641 | ||
| 1,694 | 2,037 | 2,738 | 1,665 | 1,991 | 2,640 | ||
| 1,692 | 2,035 | 2,733 | 1,664 | 1,990 | 2,639 | ||
| 1,691 | 2,032 | 2,728 | 1,664 | 1,990 | 2,639 | ||
| 1,690 | 2,030 | 2,724 | 1,662 | 1,987 | 2,632 | ||
| 1,688 | 2,028 | 2,719 | 1,660 | 1,984 | 2,626 | ||
| 1,687 | 2,026 | 2,715 | 1,659 | 1,982 | 2,621 | ||
| 1,686 | 2,024 | 2,712 | 1,658 | 1,980 | 2,617 | ||
| 1,685 | 2,023 | 2,708 | 1,657 | 1,978 | 2,614 | ||
| 1,684 | 2,021 | 2,704 | 1,656 | 1,977 | 2,611 | ||
| 1,683 | 2,020 | 2,701 | 1,655 | 1,976 | 2,609 | ||
| 1,682 | 2,018 | 2,698 | 1,653 | 1,972 | 2,601 | ||
| 1,681 | 2,017 | 2,695 | 1,651 | 1,969 | 2,596 | ||
| 1,680 | 2,015 | 2,692 | 1,650 | 1,968 | 2,592 | ||
| 1,679 | 2,014 | 2,690 | 1,649 | 1,967 | 2,590 | ||
| 1,679 | 2,013 | 2,687 | 1,649 | 1,966 | 2,588 |
ТАБЛИЦА 2
Критические значения χ²-критерия
| df | df | ||||||
| р≤0,1 | р≤0,05 | р≤0,01 | |||||
|
|
|
