 |
Структурная схема САР с П-регулятором
|
|
|
|
Рисунок 10 – Структурная схема САР с П-регулятором
Рисунок 11 – Схема s-модели САР с П-регулятором
Рисунок 12 – Переходная характеристика САР с П-регулятором
Переходная характеристика, полученная по s-модели САР с П-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена верно.
Оценка управляемости САР с П-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет следующий вид:
|
Script 13:
>> Y1=[B1 A1*B1 A1^2*B1]
Y1 =
0 0 1.0000
0 1.0000 -0.4417
1.0000 -0.4417 0.0771
>> rY1=rank(Y1)
rY1 =
3
>> dY1=det(Y1)
dY1 =
-1
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
Оценка наблюдаемости САР с П-регулятором
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
|
Script 14:
>> H1=[C1; C1*A1; C1*A1^2]
H1 =
0.0174 0.0555 0.0071
-0.0001 0.0166 0.0523
-0.0011 -0.0063 -0.0065
>> rH1=rank(H1)
rH1 = 3
>> dH1=det(H1)
dH1 =
8.5991e-007
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
Анализ САР с ПИ-регулятором
|
|
|
Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с ПИ-регулятором была получена в п. 1.4. Она имеет вид:
,
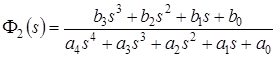где 
,
.
Порядок характеристического полинома 
. Для данной САР выбираем вторую управляемую форму или управляемое каноническое представление (УКП). Математическая модель САР описывается следующей системой векторно-матричных уравнений:
|
где 
Script 15:
>> b3=1.089;b2=8.558;b1=3.348;b0=0.2156;
>> a4=336;a3=147.1;a2=29.56;a1=4.348;a0=0.2156;
>> A2=[0 1 0 0;0 0 1 0;0 0 0 1;-a0/a4 -a1/a4 -a2/a4 -a3/a4];
>> B2=[0;0;0;1];
>> C2=[b0/a4 b1/a4 b2/a4 b3/a4];
>> D2=0;
>> sys2=ss(A2,B2,C2,D2)
a =
x1 x2 x3 x4
x1 0 1 0 0
x2 0 0 1 0
x3 0 0 0 1
x4 -0.0006417 -0.01294 -0.08798 -0.4378
b =
u1
x1 0
x2 0
x3 0
x4 1
c =
x1 x2 x3 x4
y1 0.0006417 0.009964 0.02547 0.003241
d =
u1
y1 0
Continuous-time model.
>> step(sys2);grid
Рисунок 13 – Переходная характеристика САР с ПИ-регулятором
При исользовании модели «вход-выход» и модели «вход-состояние-выход» были получены абсолютно идентичные переходные характеристики (рисунки 5 и 13), следовательно, модель «вход-состояние-выход» для САР с ПИ-регулятором рассчитана верно.
Структурная схема САР с ПИ-регулятором
Рисунок 14 – Структурная схема САР с ПИ-регулятором
Рисунок 15 – Схема s-модели САР с ПИ-регулятором
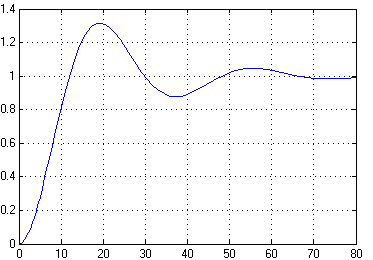
Рисунок 16 – Переходная характеристика САР с ПИ-регулятором
Переходная характеристика, полученная по s-модели САР с ПИ-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена, верно.
Оценка управляемости САР с ПИ-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет следующий вид:
|
Script 16:
>> Y2=[B2 A2*B2 A2^2*B2 A2^3*B2]
Y2 =
0 0 0 1.0000
0 0 1.0000 -0.4378
0 1.0000 -0.4378 0.1037
1.0000 -0.4378 0.1037 -0.0198
>> rY2=rank(Y2)
rY2 = 4
>> dY2=det(Y2)
dY2 = 1
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
|
|
|
|
|
|
