 |
Оценка наблюдаемости САР с ПИ-регулятором
|
|
|
|
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
|
Script 17:
>> H2=[C2; C2*A2; C2*A2^2; C2*A2^3]
H2 =
0.0006 0.0100 0.0255 0.0032
-0.0000 0.0006 0.0097 0.0241
-0.0000 -0.0003 -0.0015 -0.0009
0.0000 -0.0000 -0.0002 -0.0011
>> rH2=rank(H2)
rH2 =4
>> dH2=det(H2)
dH2 = -1.2054e-014
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
Анализ САР с ПИД-регулятором
Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с ПИД-регулятором была получена в п. 1.5. Она имеет вид:
,
где 
,
.
Порядок характеристического полинома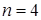 
. Математическая модель данной САР описывается следующей системой векторно-матричных уравнений:
|
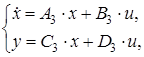
где 
,
,
,
,
.
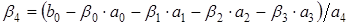Script 18:
>> b4=1.836;b3=16.13;b2=19;b1=5.77;b0=0.396;
>> a4=337.8;a3=162.1;a2=40;a1=6.77;a0=0.396;
>> v0=b4/a4;
>> v1=(b3-v0*a3)/a4;
>> v2=(b2-v0*a2-v1*a3)/a4;
>> v3=(b1-v0*a1-v1*a2-v2*a3)/a4;
>> v4=(b0-v0*a0-v1*a1-v2*a2-v3*a3)/a4;
>> A3=[0 1 0 0;0 0 1 0;0 0 0 1;-a0/a4 -a1/a4 -a2/a4 -a3/a4];
>> B3=[v1;v2;v3;v4];
>> C3=[1 0 0 0];
>> D3=v0;
>> sys3=ss(A3,B3,C3,D3)
a =
x1 x2 x3 x4
x1 0 1 0 0
x2 0 0 1 0
x3 0 0 0 1
x4 -0.001172 -0.02004 -0.1184 -0.4799
b =
u1
x1 0.04514
x2 0.03394
x3 -0.00466
x4 -0.001521
c =
x1 x2 x3 x4
y1 1 0 0 0
d =
u1
y1 0.005435
Continuous-time model.
>> step(sys3);grid
Рисунок 17 – Переходная характеристика САР с ПИД-регулятором
При исользовании модели «вход-выход» и модели «вход-состояние-выход» были получены абсолютно идентичные переходные характеристики (рисунки 7 и 17), следовательно, модель «вход-состояние-выход» для САР с ПИД-регулятором рассчитана, верно.
|
|
|
Структурная схема САР с ПИД-регулятором
Рисунок 18 – Структурная схема САР с ПИД-регулятором
Рисунок 19 – Схема s-модели САР с ПИД-регулятором
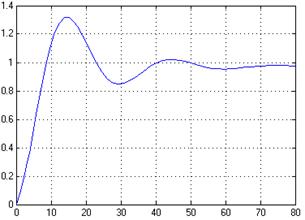
Рисунок 20 – Переходная характеристика САР с ПИД-регулятором
Переходная характеристика, полученная по s-модели САР с ПИД-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена, верно.
Оценка управляемости САР с ПИД-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет вид (15):
|
Script 19:
>> Y3=[B3 A3*B3 A3^2*B3 A3^3*B3]
Y3 =
0.0451 0.0339 -0.0047 -0.0015
0.0339 -0.0047 -0.0015 0.0005
-0.0047 -0.0015 0.0005 -0.0000
-0.0015 0.0005 -0.0000 -0.0000
>> rY3= rank(Y3)
rY3 = 4
>> dY3=det(Y3)
dY3 = -1.6937e-014
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
Оценка наблюдаемости САР с ПИД-регулятором
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
|
Script 20:
>> H3=[C3;C3*A3;C3*A3^2;C3*A3^3]
H3 =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> rH3=rank(H3)
rH3 = 4
>> dH3=det(H3)
dH3 = 1
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
Анализ нелинейной САР
Описание нелинейной САР
Cтруктурная схема нелинейной САР представлена на рисунке 21.
|
|
|
Рисунок 21 – Структурная схема нелинейной САР
Роль АР выполняет ПИ-регулятор с передаточной функцией, полученной в п. 1.4:
.
Нелинейное звено – звено с насыщением (ограничением), статическая характеристика звена изображена на рисунке 22.
Рисунок 22 – Статическая характеристика нелинейного элемента
Параметры звена с насыщением: 
.
|
|
|
