Несимметричный режим трехфазной цепи

 

Один из наиболее часто встречающихся случаев несимметричного режима трехфазной цепи получается при соединении фаз несимметричного приемника звездой без нейтрального провода или с нейтральным проводом, комплексное сопротивление которого необходимо учитывать при расчете (рис. 4,а).

Приведенная на рисунке 4,а схема имеет две нейтральные точки: симметричного генератора N и несимметричного приемника n – два узла цепи. Для расчета режима работы воспользуемся формулой межузлового напряжения. В рассчитываемой трехфазной системе комплексное значение напряжения между нейтральными точками приемника и генератора называется напряжением смещения нейтрали. Это напряжение

. (11)

С учетом равенств

(12)

 

 

Рисунок 4

 

где - фазный коэффициент,-

перепишем (11) в виде

. (13)

Фазные напряжения приемника определяются по второму закону Кирхгофа:

(14)

По закону Ома фазные токи и ток в нейтральном проводе соответственно равны

(15)

Распределение напряжений между фазами несимметричного приемника, фазы которого соединены звездой, показано на потенциальной диаграмме (рис. 4,в).

При построении потенциальной диаграммы равный нулю потенциал выбран у нейтральной точки N генератора, которая служит началом отсчета. Из начала отсчета построены три вектора фазных ЭДС генератора 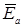, , . Концы этих векторов определяют комплексные значения потенциалов , , линейных проводов при , а, следовательно, и линейных напряжений , , 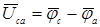. При симметричном приемнике нет смещения нейтрали, т.е и потенциал нейтральной точки приемника . Поэтому на диаграмме потенциал нейтральной точки приемника совпадает с нейтральной точкой генератора . При несимметричном приемнике смещение нейтрали не равно нулю. Поэтому потенциал нейтральной точки приемника смещается относительно потенциала нейтральной точки генератора , т.е. из центра треугольника линейных напряжений.

Рассмотрим простейший случай приемника с активными сопротивлениями фаз r_a и r_b = r_c = r при отсутствии нейтрального провода (рис. 4,б). Проводимости фаз b и c одинаковые: g_b = g_c = g = 1/r, а проводимость g_a = 1/r_a фазы а изменяется от 0 до ∞. Приняв g_a/g = m, определим смещение нейтрали:

. (16)

При изменениях проводимости g_a в пределах от нуля до бесконечности множитель при ЭДС 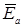остается действительной величиной. Следовательно, напряжение смещения нейтрали совпадает по фазе с ЭДС 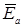при m > 1, а при m < 1 их фазы отличаются на π (рис. 4,в). В частности, при размыкании фазы а, т.е. g_a = 0 или r_a → ∞ и m = 0, смещение нейтрали

. (17)

При этом фазные напряжения приемника

(18)

При g_a → ∞ или r_a = 0, т.е. при коротком замыкании точек а и n, , , .

Потенциал нейтральной точки приемника может сместиться далеко за пределы треугольника линейных напряжений, если проводимости фаз приемника, соединенных звездой без нейтрального провода, различны по характеру.

Соединение приемников треугольником

 

Как видно из схемы, приведенной на рис. 1,а, каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению:

. (1)

Если не учитывать сопротивления проводов сети, то напряжения приемника можно считать равными линейным напряжениям источника.

Применяя первый закон Кирхгофа к узловым точкам а, b, c, определим соотношения между линейными и фазными токами:

. (2)

Используя полученные соотношения и имея векторы фазных токов, нетрудно построить векторы линейных токов.

 

Симметричная нагрузка

В отношении любой фазы справедливы все формулы, полученные для однофазных цепей. Например,

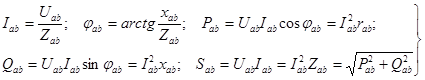. (3)

Очевидно, при симметричной нагрузке

(4)

Векторная диаграмма фазных и линейных напряжений, а также фазных токов при симметричной активно-индуктивной нагрузке приведена на рис. 1,б. Там же в соответствии с выражениями (2) построены векторы линейных токов. Из полученных выражений и векторной диаграммы следует, что при симметричной нагрузке существуют симметричные системы фазных и линейных токов.

Векторы линейных токов чаще изображают соединяющими векторы соответствующих фазных токов, как показано на рис. 1,в.

На основании векторной диаграммы

 

. (5)

Для определения мощностей трехфазного приемника при симметричной нагрузке можно воспользоваться формулами, полученными для соединения звездой.

 

 

Рисунок 1

 

Несимметричная нагрузка

 

Как и при соединении звездой, в случае соединения треугольником однофазные приемники делят на три примерно равные в отношении мощности группы. Каждая группа подключается к двум проводам, между которыми имеется напряжение, отличающееся по фазе от двух других напряжений сети (рис. 2) В пределах каждой группы приемники соединяются параллельно.

 

 

Рисунок 2

 

Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также фазные мощности можно определить по формулам (3). при несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности в общем случае будут различными.

Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе са – активно-емкостная (рис. 3,а) приведена на рис. 3,б. Построение векторов линейных токов выполнено в соответствии с (2).

Для определения мощностей всех фаз следует пользоваться формулами

. (6)

Если кроме фазных токов требуется определить линейные токи, то задачу следует решать в комплексной форме. Для этой же цели можно воспользоваться векторной диаграммой.

При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме фазные напряжения, а также полные сопротивления фаз. после этого нетрудно по закону Ома определить фазные токи.

 

а) б)

 

Рисунок 3

 

Линейные токи определяются через фазные с помощью выражений (2).

Комплексным методом можно воспользоваться и для определения фазных мощностей. Например, мощности фазы ab равны

. (7)

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: