 |
Методы анализа сложных электрических цепей
|
|
|
|
Расчет сложных электрических цепей постоянного тока
План лекции
1. Метод контурных токов.
2. Пример использования метода контурных токов.
3. Общие соотношения между контурными токами, сопротивлениями и ЭДС цепи произвольной конфигурации.
4. Преобразование параллельного соединения ветвей с источниками ЭДС и источниками тока.
5. Принцип наложения.
6. Свойство взаимности.
7. Теорема о компенсации.
8. Двухполюсники.
9. Теорема об активном двухполюснике.
10. Применение теоремы об активном двухполюснике и принципа наложения.
Метод контурных токов
Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь к = (в – у + 1) независимых уравнений, составленных на основании второго закона Кирхгофа, воспользовавшись методом контурных токов (здесь в – число ветвей, у – число узлов).
Для иллюстрации применения метода контурных токов рассмотрим схему на рис. 1.1,а с шестью ветвями и четырьмя узлами.
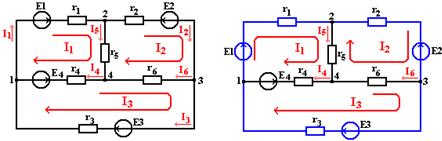
а) б)
Рисунок 1.1
Прежде чем составлять уравнения по второму закону Кирхгофа, надо выбрать взаимно независимые контуры так, чтобы одна из ветвей каждого контура входила только в этот контур.
Для правильного выбора независимых контуров введем дополнительные понятия. Деревом графа (схемы) называется совокупность ветвей, соединяющих все узлы, но не образующих ни одного контура. Между двумя узлами дерева существует только один путь графа – непрерывная последовательность ветвей между заданными двумя узлами при условии, что каждый узел встречается не более одного раза. Наличие хотя бы двух разных путей между двумя узлами дерева, очевидно, приводит к образованию контура. Если число узлов схемы и ее графа – у, то число ветвей дерева равно у – 1, т.к. из у ветвей можно всегда составить контур. Ветвью связи (связью, главной ветвью или дополнением дерева) называется любая ветвь, не входящая в состав дерева. Все ветви схемы, не входящие в состав дерева и называемые ветвями связи, дополняют дерево до полной схемы.
|
|
|
Взаимно независимые контуры получаются, если в каждый контур войдет одна ветвь связи, действительный ток которой будет равен соответствующему контурному току. Ветви с идеальными источниками ЭДС и без сопротивлений обычно включают в состав дерева, а ветви с источниками тока относят к ветвям связи. Ветви с идеальными источниками ЭДС и сопротивлениями могут входить как в состав ветвей дерева, так и в состав ветвей связи. На рис..1,б элементы ветвей дерева изображены четными линиями, а элементы ветвей связи – синими. Из приведенной схемы видно, что при выбранном дереве токи в ветвях связи (I1, I2, I3), совпадающие с контурными токами равны действительным токам этих ветвей.
Для схемы на рис. 1.1,а по первому закону Кирхгофа:
 ; (1.1)
; (1.1)
 ; (1.2)
; (1.2)
 . (1.3)
. (1.3)
На основании второго закона Кирхгофа:
 (1.4)
(1.4)
Исключая, используя выражения (1.1) – (1.3), из уравнений (1.4) токи всех ветвей дерева, общие для нескольких контуров, получим:
 (1.5)
(1.5)
В соответствии с уравнениями (1.5) можно принять, что каждый из токов I1, I2, I3 замыкается через соответствующую ветвь связи в одном из контуров и назвать такие токи контурными. Напряжения на сопротивлениях любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежного контуров. Например, в контуре с сопротивлениями r1, r5, r4 разность ЭДС Е1 – Е4 равняется сумме трех напряжений: от собственного контурного тока I1 на всех сопротивлениях этого контура и от токов I2 и I3 соответственно на сопротивлениях r5 и r4. Действительные токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:
|
|
|
 (1.6)
(1.6)
|
|
|


