 |
Пример использования метода контурных токов
|
|
|
|
В качестве примера рассмотрим схему на рис. 1.2.
Рисунок 1.2
На основании второго закона Кирхгофа:
(1.7)
Пользуясь первым уравнением Кирхгофа, исключим из полученных уравнений токи I5, I4, I6. Тогда
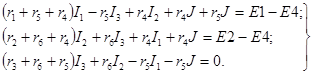(1.8)
Из уравнений (1.8) следует, что в рассматриваемом случае ток J как бы замыкается по ветвям с сопротивлениями r5 и r4, дополняющими ветвь с источником J до замкнутого контура.
Обозначив в уравнениях (1.8) составляющие напряжений r4J и r5J соответственно ET4 и ЕТ5, можно записать их в виде:
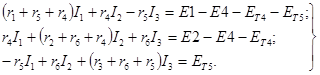(1.9)
Необходимо отметить, что перенос слагаемых r4J и r5J из левой части в правую часть уравнений (1.9) и замена этих напряжений на схеме ЭДС ET4 и ЕТ5 иллюстрирует применение теоремы о компенсации, которая позднее будет рассмотрена более подробно.
Уравнениям (1.9) соответствует эквивалентная схема (рис. 1.3,а), на которой источник тока J заменен источниками ЭДС ET4 = r4J и ЕТ5 = r5J. При этом токи в ветвях с сопротивлениями r1 и r5 не равны соответствующим токам в ветвях заданной схемы и отличаются от них на ток J источника тока.
Иначе говоря, после определения контурных токов I1, I2, I3 необходимо для вычисления токов I4, I5 в ветвях заданной схемы записать уравнения по первому закону Кирхгофа именно для заданной схемы:
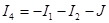; (1.10)
. (1.11)
Аналогично можно показать, что если принять ток J замыкающим по ветви с сопротивлением r1, то получится новая эквивалентная схема (рис. 1.3,б). Контурный ток в эквивалентной схеме I1 не равен действительному току I1 в заданной схеме отличается от него на ток J.
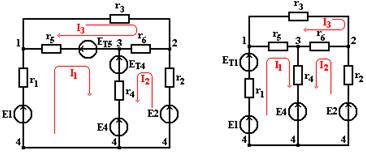
а) б)
Рисунок 1.3
При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки. Положительные направления контурных токов можно выбирать и произвольно, т.е. независимо от положительных направлений токов в ветвях.
|
|
|
Общие соотношения между контурными токами, сопротивлениями и ЭДС цепи произвольной конфигурации
Для схемы, имеющей k независимых контуров, уравнения, аналогичные (1.4), запишутся в виде
(1.12)
В этих уравнениях сопротивление с двумя одинаковыми индексами (вида rmm) называется собственным сопротивлением контура m, а сопротивление вида rmk = rkm (c двумя различными индексами) называется общим сопротивлением контуров k и m. Правые части уравнений называются контурными ЭДС. Каждая из контурных ЭДС вида Еmm равна алгебраической сумме ЭДС всех источников в ветвях контура m. Положительные знаки в каждом уравнении (1.12) должны быть взяты для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.
Решая систему уравнений (1.12) при помощи определителей относительно любого из токов, например Im, получаем:
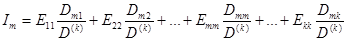, (1.13)
где
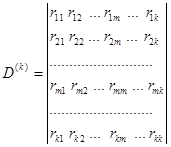- определитель системы уравнений; (1.14)
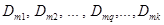- алгебраические дополнения определителя 
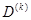, причем 
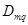получается из 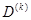путем вычеркивания m-ного столбца и q-той строки и умножения полученного определителя на (-1)m+q. При этом сопротивления вида rmm и rkm нужно записывать в выражении (1.14) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1.12).
Для решения общей задачи расчета неизвестных токов во всех ветвях линейной электрической цепи можно выбрать один из двух основных методов расчета: узловых потенциалов или контурных токов.
Метод узловых потенциалов целесообразно использовать, когда число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров (у – 1 < k), а метод контурных токов при у -1 > k.
|
|
|
|
|
|
