Мощность цепи переменного тока

Мгновенная мощность электрической цепи определяется по выражению p = u*i, где u и i – мгновенные напряжение на зажимах цепи и ток в ней.

Энергия, доставляемая в цепь, равна произведению времени, в течение которого энергия доставляется, на среднее значение мощности за рассматриваемый промежуток времени. Важной величиной является среднее значение мощности за период переменного тока:

. (3.19)

Это выражение мощности справедливо для любых периодических функций напряжения и тока.

Пусть .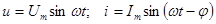

Среднее значение мощности за период

. (3.20)

Т.к. интеграл второго члена подынтегрального выражения равен нулю, то

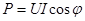. (3.21)

Средняя мощность за период, подобно мощности цепи постоянного тока, определяет энергию, подводимую к цепи за одну секунду. Поэтому ее называют активной мощностью. Множитель cosφ называется коэффициентом мощности.

Цепь с резистивным элементом. В этом случае cosφ = 1 и φ = 0. Мгновенная мощность

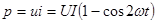. (3.22)

Средняя мощность равна произведению действующих значений напряжения и тока P_ср = UI. Наибольшее значение мощности Р_max = 2UI, наименьшее P_min = 0.

Цепь с идеальной катушкой индуктивности. В этом случае ток отстает от напряжения на угол φ = π/2. Тогда

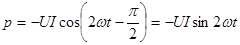. (3.23)

Средняя мощность равна нулю.

Если переменный ток изменяется по гармоническому закону

,

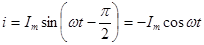то энергия магнитного поля

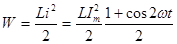(3.24)

также меняется гармонически от нуля до 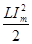с угловой частотой 2ω.

В цепи происходит непрерывный обмен энергией между источником энергии и цепью, с которой связано магнитное поле.

Цепь с конденсатором. Подобно цепи, содержащей катушку индуктивности, в цепи с конденсатором имеет место непрерывный обмен энергией между источником энергии и цепью, в которой доставляемая энергия преобразуется в энергию электрического поля конденсатора. Ток цепи опережает напряжения на угол φ = π/2.

Средняя мощность за период равна нулю; наибольшее значение энергии, запасенной в электрическом поле,

. (3.25)

Цепь с резистивным элементом, катушкой индуктивности и конденсатором. При преобладании индуктивного сопротивления в цепи ток отстает от напряжения на угол φ, а при преобладании емкостного – опережает напряжение.

Мгновенная мощность цепи:

(3.26)

Мощность Р = UIcosφ является активной мощностью, а переменная мощность, идущая на увеличение магнитного или электрического полей или поступающая обратно в цепь: Q = UIsinφ, называется реактивной мощностью. Активная мощность выражается в ваттах (Вт), а реактивная – в вольт-амперах реактивных (вар).

Мощность, имеющая амплитуду

, (3.27)

называется полной мощностью и выражается в вольт-амперах (ВА).

Мощность цепи в символическом виде.

Комплексная мощность цепи

. (3.28)

Условие резонанса напряжений

 

Резонанс в схеме последовательного соединения R, L, C (рис. 4.1,а) называется резонансом напряжений.

 

а) б)

 

Рисунок 4.1

 

При резонансе ток в цепи должен совпадать по фазе с ЭДС. Это возможно, если входное сопротивление схемы

(4.1)

будет чисто активным. Условие наступления резонанса в схеме на рис. 4.1,а

, (4.2)

где ω₀ – резонансная частота.

При этом

. (4.3)

Напряжение на индуктивности при резонансе равно напряжению на емкости:

. (4.4)

Отношение

(4.5)

называется добротностью резонансного контура, а величина - характеристическим сопротивлением контура.

Рассмотрим характер изменения тока I и напряжений U_L и U_С в функции от ω.

Ток в цепи

. (4.6)

При изменении ω меняется реактивное сопротивление цепи :

при ω → 0 сопротивление х → ∞ и ток I → 0;

при сопротивление х = 0 и ток I = E/R;

при ω → ∞ сопротивление х → ∞ и ток I → 0.

Напряжение на индуктивности

. (4.7)

При ω → 0 напряжение U_L → 0;

при ω → ∞ напряжение U_L → Е.

При ω → 0 напряжение на емкости → Е;

при ω → ∞ U_С → 0.

 

 

Условие резонанса токов

 

Явление резонанса в схеме, образованной двумя параллельными ветвями с разнохарактерными реактивными сопротивлениями (рис. 5.1,а), называется резонансом токов.

 

а) б)

 

Рисунок 5.1

 

Первая ветвь имеет активное сопротивление R₁ и индуктивное ωL, а вторая ветвь – активное R₂ и емкостное 1/ωС.

Ток первой ветви отстает от напряжения 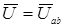(рис. 5.1,б):

. (5.1)

Ток второй ветви опережает напряжение:

. (5.2)

Ток в неразветвленной части цепи:

. (5.3)

По определению резонансного режима ток должен совпадать по фазе с напряжением , т.е. при условии, что сумма реактивных проводимостей равна нулю:

.

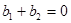Учитывая, что

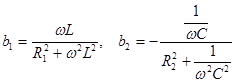, (5.4)

условие наступления режима резонанса токов можно записать:

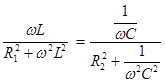. (5.5)

На рис. 5.1,б изображена диаграмма для резонансного режима. Из (5.5) следует, что если R₂ = 0, то резонанс наступит при

. (5.6)

В еще более частном случае, когда R₂ = 0 и R₁ << ωL, резонанс наступит при

. (5.7)

Резонанса можно достичь путем изменения ω, L, C или R₁ и R₂. Ток в неразветвленной части схемы по величине может быть меньше, чем токи в ветвях схемы. При R₂ = 0 и R₁ ≈ 0 ток I может оказаться ничтожно малым по сравнению с токами I₁, I₂.

В идеализированном (практически не выполнимом) режиме работы, когда R₁ = R₂ = 0, ток в неразветвленной части схемы равен нулю, а ее входное сопротивление равно бесконечности.

В формулу (5.5) входят пять величин. Если определять из нее L или C, то может оказаться, что для искомой величины будут получены одно или два действительных значения, либо мнимое значение.

Получение двух действительных значений для L и С свидетельствует о том, что при неизменных четырех параметрах вследствие изменения пятого параметра можно получить два резонансных режима.

Получение мнимых значений L и С свидетельствует о том, что при данных сочетаниях параметров резонанс невозможен.

Определим из (5.5) ω:

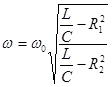, (5.8)

где ω₀ – резонансная частота в контуре без потерь (при R₁ = R₂ = 0).

Т.к. угловая частота действительна и положительна, то числитель и знаменатель в выражении (5.8) должны иметь одинаковые знаки. Это имеет место при:

. (5.9)

При R₁ = R₂ частота ω = ω₀.

При , (5.10)

т.е. ω в случае (5.10) получается величиной неопределенной. Физически это означает, что резонанс может возникать при любой частоте. Сопротивление параллельного контура при этом чисто активное, равное R₁.

 

 

ЛИТЕРАТУРА

 

Основная

 

8. Касаткин В.С., Немцов М.В., Электротехника. - М.; Энергоатомиздат, 2000.

9. Основы промышленной электроники /Под ред. В.Г. Герасимова.- М.: Высшая школа, 1985.

10. Основы теории цепей; Учебник для ВУЗов. /В.П.Бакалов и др. 2-ое изд. перераб. и доп. – М.; 2000.

11. Сборник задач по электротехнике и основам электроники / Под ред. В.Г. Герасимова.- М.: Высшая школа, 1987.

12. Прянишников В.А. Электроника. - СПб; Корона принт, 2002.

13. Хоровиц П., Хилл У.. Искусство схемотехники.- М.:Мир, 1997.

14. Амочаева Г.Г. Электронный конспект лекций.

 

Дополнительная

 

6. Алексеенко А.Г., Шагурин Н.И. Микросхемотехника. Учебное пособие для вузов.- М.: Радио и связь, 1990.

7. Жеребцов И.П. Основы электроники.- Л.: Энергоатомиздат, 1990.

8. Попов В.П., Основы теории цепей.- Учебник для ВУЗов.- 3-е изд. испр.-М.: Высшая школа, 2000.

9. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. в 2-х томах, Под ред. Д.И. Панфилова ДОДЭКА, 1999.-т.1-Электроника.

10. Электротехника/Ю.М. Борисов, Д.Н. Липатов, Ю.Н. Зорин. Учебник для вузов.- 2-е изд., перераб. и доп.- М.: Энергоатомиздат, 1985.

Лекция №5 – 6

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: