 |
Максимальная неаляйсинговая частота
|
|
|
|
Каждый объект, залегающий на глубине, будет иметь максимально возможную неаляйсинговую частоту, Fmax (с периодом Т) до миграции, которая зависит от скорости формирования, Vint сразу же над объектом, значение глубины, угол q, и размер бина, b (рис. 2.9).
sin q = (Vint * t/2)/b, заменяем t = T/2
= (Vint * T/4)/b заменяем, T = 1/Fmax
= Vint / (4 * b * Fmax)
Заметьте, что мы используем интервальную скорость сразу же над горизонтом, предпочтительней, чем среднюю скорость, чтобы избежать чрезмерного ограничения размера бина (см. Bee, et al., 1994 для обсуждения). Следовательно,
Fmax = Vint / (4 * b * sin q)
Fmax =3000 м/сек ¸ (4 * 25 м * sin 15°) = 116 Гц
или
Fmax = 10000 футов/сек ¸ (4 * 82 фута * sin 15°) = 118 Гц
или решая для размера бина b:
размер бина = Vint/(4 * Fmax * sin q)
например, если Fmax = 80 Гц
размер бина = 3000 м/сек ¸ (4 * 80 Гц * sin 15°) = 36 м
или
размер бина = 10000 футов/сек ¸ (4 * 80 Гц * sin 15°) = 120 футов
Любые частоты на объекте, которые выше данного значения, будут подвержены аляйсингу до миграции. Другими словами, истинная глубина объекта будет ограничена частотами, меньшими, чем эта величина. Вышеприведенные уравнения основываются на двух отсчетах на каджую длину волны. Многие компании в настоящее время используют более точные требования в 3 или 4 (или даже не целые значения, такие как 2.8), тем самым, снижая размер бина.
Заметьте, что процесс миграции будет снижать частоты на всех глубоко залегющих объектах (чем круче глубокозалегающий горизонт, тем ниже частоты после миграции). Любой аляйсинг частот до миграции может выглядеть как дисперсия частот после миграции из-за использования особого алгоритма. Выберите размер бина, чтобы успешно сохранить некоторую максимальную частоту вашего выбора подвергнутую миграции.
|
|
|
Связь между размером бина, b и Fmax после миграции задается той же самой формулой, что и приведенная выше, но при этом необходимо заменить sin q на tan q.
Метрический пример
Используя формулу, Fmax = Vint / (4 * b * sin q), рассчитайте Fmax для следующих трех групп чисел (Vint = 3000 м/сек):
| Dip В градусах | B В метрах | Fmax, Гц |
| = | ||
| = | ||
| = |
Используя формулу, размер бина = Vint / (4 * Fmax * sin q), рассчитайте размер бина b для следующих групп чисел (Vint = 3000 м/сек):
| Dip В градусах | Fmax, Гц | B В метрах |
| = | ||
| = | ||
| = |
Общий пример
Используя формулу, Fmax = Vint / (4 * b * sin q), рассчитайте Fmax для следующих групп чисел (Vint = 10000 футов/сек):
| Dip В градусах | B В футах | Fmax, Гц |
| = | ||
| = | ||
| = |
Используя формулу, размер бина = Vint / (4 * Fmax * sin q), рассчитайте размер бина b для следующих групп чисел (Vint = 10000 футов/сек):
| Dip В градусах | Fmax, Гц | B В футах |
| = | ||
| = | ||
| = |
Таблица Alias Частот (метрическая)
Таблица 2.2 рассчитывает Fmax. Vint=3000 m/sec
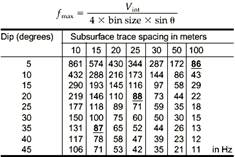
Таблица 2.3 рассчитывает размер бина B

Таблица 2.4. рассчитывает Fmax. Vint=10 000 ft/sec

Таблица 2.5 рассчитывает размер бина B

Горизонтальное разрешение
До миграции две дифракции не могут быть разрешены, елси они находятся ближе, чем первый диаметр зоны Френеля. Это обычно очень большое значение (500 м или больше) и означает, что на суммарном разрезе ОСТ небольшие дефекты и т.д. могут быть легко не замечены. После миграции горизонтальное разрешение зависит от максимальной частоты, которая отражается от интересующей зоны.
За прошедешие несколько лет много определений и формул для горизонтального разрешения были опубликованы.
| Denham (1980) | RH = RV / sin q, где q - это максимальный угол луча, способствующего миграции |
| Claerbout (1985) | Разрешающая способность обычно определяется как около половины эффективой длины волны |
| Embree (1985) | dXr = 0.3 * V / (Fmax * sin q) |
| Freeland & Hogg (1990) | RL = RV = V/2B, (т.е. период времени = половина ширины полосы частот) |
| Ebrom et al (1995) | RL = lmin/4 * sin q, где lmin = 1/Fmax и q = acrtan (L/2)/Z, где L/2 – это половина длины линии и Z – глубина целевого горизонта |
| Vermeer (1996) | RX = V / 4 * Fmax * sin q Вермеер объясняет это как Vmin / 4 * Fmax, где Vmin – это минимальная кажущаяся скорость продольной волны |
Общепризнано, что достигаемое горизонтальное разрешение (после миграции) равно вертикальному разрешению – допуская первоначально широкий ореол миргации. Это (оно) также зависит от максимальной частоты. Не каждый согласится с таким определением разрешения – это половина длины доминирующей волны (Claerbout, Freeland & Hogg) или что это одна четверть минимальной длины волны (Ebrom, Vermmer) или где-то посередине (Embree)?
|
|
|
Теоретически правильный ответ принадлежит Вермееру, но можем ли мы допустить это? Используя его формулу для ограниченной цели в 4000 м/сек, ореол миграции = 30 градусов и максимальная частота в 40 Гц мы получаем RX = 12.5 м. В большинстве случаев на практике, вы можете сказать, что ореолы миграции в 30 градусов приемлемы (личное сообщение – G. Vermeer, 1998) и такие частоты могут не быть такими высокими, как мы хотели бы полагать, т.е. вы можете прийти от минимального значения разрешения в 4 точки на длину волны максимальной частоты до 2 точек на длину волны доминирующей частоты (разница фактора в 4!).
Это тяжелый вопрос и по этому поводу было издано много статей. Предыдущая формула, относящая размер бина к максимальной неаляйсинговой частоте для определенного падения должна рассматриваться как лучший вариант (т.е. не делайте размер бина больше, чем Vint / (4 * Fmax * sin (dip)). Заметьте, что q имеет различные значения в разных формулах. В случае с горизонтальным разрешением, q - это ореол миграции. В случае с максимальной неаляйсинговой частотой, q - это геологический угол падения.
Если у вас небольшие углы падения (меньше чем 10 градусов) формула для горизонтального разрешения является способом визуального определения количества разобщенных объектов. Во многих случаях, эти формулы выдают вам размеры бина в диапазоне от 5 до 10 м (15-30 футов). Что хочет интерпретатор? Мы постоянно видим большие размеры бина: от 25 до 35 м, что свойственно для 3D участков (80-110 футов). Таким образом, меньшие размеры бина покажут больше деталей вдоль горизонта, но нужно ли нам допускать это?
|
|
|
В данном курсе, мы допустим, что горизонтальное разрешение будет лежать между одной четвертью и одной половиной доминирующей длины волны. Доминирующая частота измеряется непосредственно с сейсмического разреза: сколько максимумов находится в промежутке времени? Теоретически, такая величина – это от 2 до 4 раз «максимально достигаемого разрешения».
Основное эмпирическое правило: Размер бина = Vint / (N * Fdominant), где N меняет свое значение от 2 до 4.
Чтобы выразить это другим способом, предположим, что доминирующая частота Fdominat нашего целевого горизонта составляет 50 Гц. Если интервальная скорость сразу же над нашим горизонтом составляет 3000 м/сек (10000 футов/сек), тогда пространственная длина волны, l dominant, составит 3000 м/сек ¸ 50 Гц, т.е. 60 метров (10000 футов/сек ¸ 50Гц, т.е. 200 футов).
Размер бина = Vinterval / (2 * Fdominant)
Напрмер, размер бина = 10000 футов/сек/ (2 * 50 Гц) = 100 футов (или 50 футов используя N = 4)
Используя примеры последних нескольких страниц, горизонтальное разрешение определяет диапазон возможных размеров бина, начиная с минимальных 15 м (50 футов) до максимально приемлемого размера бина в 30 м (100 футов) (табл. 2.6).
Имеется небольшая точка зрения в выборе размера бина меньшего, чем минимальное горизонтальное разрешение. Если бы у нас были меньшие бины, они бы ничего не добавили к содержимому того, что мы видим. Соответственно, если бы мы имели большие бины, имелась бы опасность, что некоторые объекты не имели бы разрешенности по горизонтали.
Размер бина = ½ длины волны доминирующей частоты Fdom
Размер бина < ½ длины волны Fmax дает чрезмерную выборку, не добавляя никакой информации
Размер бина > ½ длины волны Fdom дает пространственный аляйсинг, следовательно, теряется информация
Таблица 2.6 Выбор размера бина
| Параметр | Размер бина |
| Размер целевого горизонта | 33 м (100 футов) |
| Макс. Антиаляйсинговая частота | 36 м (120 футов) |
| Латеральное разрешене | 15 - 30 м (50 – 100 футов) |
В нашем примере мы выберем размер бина в 30 м.
|
|
|
|
|
|


