Главная | Обратная связь | Поможем написать вашу работу!

Съемки с узким и широким азимутом

Съемки с узким азимутом имеют линейное распределение выносов относительно выноса (х) (Рис. 3.5а, похоже на 2D), однако, при наличии зависимости от квадратного значения выноса (х²), распределение выноса показывает сгущение на ближних выносах (Рис. 3.5b). Заплатки узкого азимута лучше использовать для работ AVO, а также, когда присутствует достаточное количество вариантов латеральной скорости (Лансли, 1994). Считалось, что узкие заплатки также хорошо используются и для DMO, но недавние находки опровергнули это мнение (Вермеер и ал, 1995, 1998).

Съемки с широким азимутом (т.е. близкие к квадратной заплатке) имеют нелинейное распределение выносов относительно х, с утяжелением веса дальних выносов (Рис. 3.5с); однако, при наличии зависимости от квадратного значения выноса (х²), распределение линейно (Рис. 3.5d). Съемки с широким азимутом лучше использовать для скоростного анализа, ослабления кратных волн, решений статики и более равномерного направленного опробования (анализа?) приповерхностного слоя.

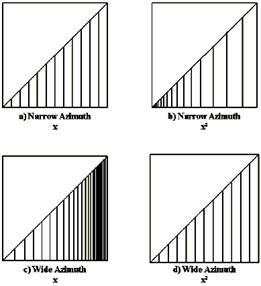
Рис. 3.5

3.4 Правило 85%

Если вы решили, что необходимо использовать съемку с широким азимутом, как же можно выбрать «лучшее» отношение большей стороны заплатки к меньшей? На текущий момент, позвольте ограничить решение квадратными заплатками, когда коэффициент отношения равен 1 (размер вдоль линии равен размеру поперек линии).

Примем круг площади = 1, с радиусом Х_мах (большой круг на Рис. 3.6). Если заплатка лежит полностью за пределами этого круга, тогда 27% каналов в заплатке используются для записи данных, что, возможно, будет обнулено! В то время как эти каналы могут иметь какое-то значение для анализов отражений волн большей длины, использование такого количества дополнительных каналов – это слишком дорого.

С другой стороны, можно уменьшить заплатку в размерах так, чтобы она лежала полностью внутри записываемого выноса, как показано малой площадью. Х_мах должно измеряться вдоль диагонали заплатки, но теперь заплатка покрывает только 64% площади объекта вашего проектирования, т.е. большого круга. Это еще одна крайность неэффективности; только несколько трасс лежат на выносах, близких к максимальному выносу вашего проектирования.

Легко говорить, что следует всегда иметь заплатку размером с большой квадрат, чтобы все время и во всех направлениях записывать до Х_мах. Однако большой квадрат является двойной площадью малого квадрата.

В некоторых случаях доступность оборудования может стать проблемой, и экономия должна быть сделана на основе использования минимального количества каналов. В таком случае мы рекомендуем «Правило 85%», как компромисс в определении коэффициента отношения заплатки относительно Х_мах.

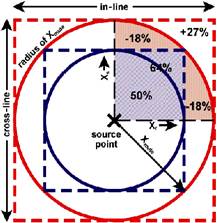
Рис. 3.6

Правило 85% - это простой способ оптимизировать площадь использованных записанных трасс и количество необходимых каналов. Это работает следующим образом:

Определить Х_мах.

Выбрать вынос вдоль линии, Х_r, равным 0,85 * Х_мах

Выбрать вынос поперек линии, Х_s, равным 0,85 * Х_r= 0,72 * Х_мах

Реальный пример:

Х_мах = 2000 м (6600 футов)

Размер вдоль линии:

Х_r= 85% * Х_мах = 1700 м (5610 футов)

Размер поперек линии:

Х_s = 85% * Х_r = 1445 м (4730 футов)

Коэффициент сжатия Х_r/X_s = 85%

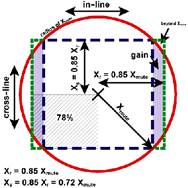
Рис. 3.7

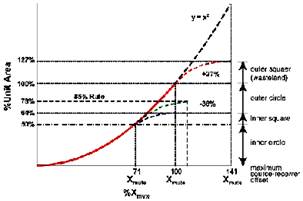
Рис. 3.8

Используемая площадь заплатки относительно круга Х_мах скачет от 64% до 78%. Только очень маленькая часть заплатки находится за пределами теоретического Х_мах. Дополнительные линии ПП дальше тех, что указаны в этой заплатке, в большинстве своем находятся за пределами используемого распределения выносов. Следовательно, предпочтительно использовать более длинный размер в направлении «вдоль линии». Размеры могут потребовать некоторое слабее уравнивание, чтобы они соответствовали прочим расчетам в проектировании 3D.

Мы выбрали круг радиуса Х_мах в качестве единицы площади (100% при Х_мах100%). На Рис. 3.8 он показан сплошной линией.

Внутренний круг (с радиусом 0,71 от Х_мах) содержит 50% площади бóльшего круга. Если заплатка полностью расположена внутри Х_мах (внутренний квадрат на Рис. 3.6), тогда кривая, описывающая эту площадь, отклоняется от шаблона у = х² на 0,71 Х_мах. Площадь этой меньшей заплатки составляет 64% единицы площади.

С другой стороны, если заплатка полностью лежит за границами круга Х_мах (больший круг на Рис. 3.6), тогда кривая, описывающая эту площадь, отклоняется от шаблона у = х². Площадь большой заплатки составляет 127% единицы площади, двойная площадь меньшей заплатки!

Заплатка, использующая правило 85%, охватывает 78% единицы площади, описанной кругом Х_мах. Площадь, которую покрывает данная заплатка, составляет только на 22% больше, чем заплатка меньшего квадрата, которая лежит полностью внутри круга. Заплатка, использующая правило 85% - это превосходный компромисс для проектирования заплатки.

Зона Френеля

Зона Френеля – это та часть отражателя, от которого энергия может достичь детектора в пределах половины длины волны первой отражаемой энергии. (Шерифф, 1991).

Рассмотрим Рис. 3.9, с источником в S. Энергия из приповерхностной точки 0 приходит за t₀ = 2 * z₀ / v_rms. Допустим, что волновой фронт продвигается шагами в ¼ длины волны, λ. Энергия из точки А, или А’, достигнет приемника за время t₁ = 2 ((z₀/V_rms) + (λ/V_int)). Энергия, приходящая за временной интервал (t₁ – t_О), интерферирует конструктивно.

Отражающий диск АА’ называется первой зоной Френеля (Шерифф, 1991). Две отражающие точки, которые попадают в эту зону, обычно считаются неразличимыми, т.к. наблюдаются у поверхности земли. Радиус зоны Френеля, r_f, для вертикального падения приблизительно:

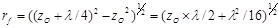
приблизительно равно

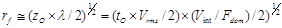
или упрощённо до:

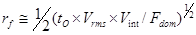
где F_dom – рассматриваемая доминантная частота.

На более низких частотах, например, F_min, зона Френеля становится больше, в то время как на больших частотах, например F_max, зона Френеля уменьшается. Такой вывод следует из подхода Йилмаза (1989), но он дифференцирует термины скорости в V_int и v_rms. Для ненулевого выноса, структура и угол наклона влияют на форму зоны Френеля. Линдсли (1989) выделяет, что зона Френеля становится как-то меньше для положительных структур, типа рифов или антиклиналей, и как-то больше для отрицательных структур, типа синклиналей.

Обычно, это эффект второго порядка, кроме случаев, когда структуры похожего масштаба к глубине.

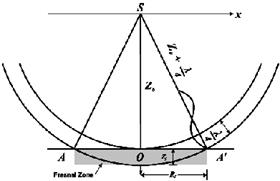
Рис. 3.9

Вертикальная мощность зоны Френеля, z_f:

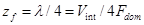
Выражая это временем, двусторонняя временная (?) мощность зоны Френеля, t_f, становится:

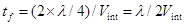где λ – это длина волны доминантной частоты.

Диаметр зоны Френеля определяет латеральное разрешение перед миграцией. В контексте дифракции, латеральное разрешение зависит от способности различать две смежные дифракции. Т.к. миграция – это процесс, который разрушает дифракции, стоит подумать, что миграция увеличивает пространственное разрешение. Плоскость наблюдения продолжается вниз и приближается к точкам отражения. Следовательно, зона Френеля уменьшается (Йилмаз, 1987). Миграция данных 3D проявляет склонность к разрушению диаметра зоны Френеля до, приблизительно, ½ длины доминантной волны, в то время как миграция данных 2D будет только сопровождать ее в направлении сейсмической линии (Линдсли, 1989).

Т.к. зона Френеля лежит частично за пределами съемок, возле краев, миграция выявит нежелаемые изображения. Это особенно важно, когда углы лицензионных блоков «подстреляны».

Дифракции

Дифракции, которые случаются там, где представлены острые геологические границы, такие как, нарушения, простираются гораздо ниже нарушения (в обоих направлениях, перпендикулярно нарушению). Ореол миграции и дифракции значительно добавят в поверхностное покрытие, которое необходимо, чтобы должным образом получить приповерхностное изображение. Следовательно, эти расчеты необходимо сделать до начала любого проектирования 3D.

Анатомия дифракции

Когда источник энергии достигает прерывности приповерхностной точки (точка дифракции), энергия может быть направлена наверх к поверхности под всеми углами. Где бы на поверхности ни был расположен приемник, он примет отражение в момент, соответствующий времени, которое необходимо, энергии источника, чтобы дойти до точки, плюс время, необходимое для возврата назад (см. Раздел 2.8.3.2). Сбор всех различных отражений называется дифракцией и имеет некоторые интересные свойства:

Площадь наверху дифракции с мощностью равной ¼ длиной волны доминантной частоты (или двойному дельта времени, равной ½ доминантной частоты) в целом именуется первой зоной Френеля.

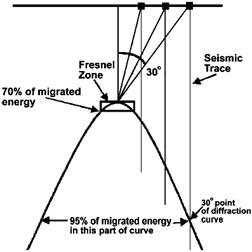
Рис. 3.10

Другие точки на дуге дифракции соответствуют различным лучам, выходящим из точки к поверхности под различными углами. Следовательно, части кривой около их верхушки соответствуют нижним отложенным углам, а части кривой более длинных двойных времен соответствуют более крутым углам. Асимптота кривой дифракции определяется с помощью 2/V, где V – это среднеквадратическая скорость на вершине дифракции.

После миграции кривая дифракции (или на самом деле, форма колокола в 3D) разрушается, не совсем до пика, как мы видели ранее, но до небольшой волны наибольшей частоты во времени и пространстве. Если мы решили использовать только часть дифракции, завершение не будет совсем полным, и ответ будет содержать только фракцию правильной энергии.

Использование только части дифракции первой зоны Френеля дает нам 70% энергии для полномигрированного результата (с углом разветвления = 15°).

Использование обеих сторон дифракции до угла разветвления (30°) дает нам примерно 95% полномигрированного результата (сравните, Рис. 3.10). Точное количество (например, 95%, 96%,…) зависит от скоростей и глубин дифракции. Поэтому нам нет необходимости в полной дифракции, чтобы получить полезный мигрированный результат.

Эмпирическое правило: Ореол миграции должен лежать между размером радиуса первой зоны Френеля и выносом, соответствующим 30-градусной точке кривой дифракции, с предпочтением, отдаваемым большим значениям.

Ореол миграции

Миграция необходима, чтобы поместить понижающиеся горизонты и нарушения в их соответствующие перспективы. При расстановке границ съемки полнократная площадь должна быть увеличена, чтобы получить апертуру миграции. Значение увеличения не всегда одно и тоже в направлении понижения и поднятия. Понижающиеся горизонты требуют, чтобы ореол миграции равнялся следующей формуле:

MA = Z tan Θ

Где MA = ореол миграции

Z = глубина

Θ = угол понижения (истинный геологический угол)

Например, МА = 2 000 м х tan20° = 728 м

Или МА = 6500 футов х tan20° = 2 400 футов

Предполагая, что геометрия – путь прямого луча, если необходимо записать отражения от горизонта понижающегося на 20°, необходимо добавить 728 м (2 400 футов) как апертуру миграции. Однако, если необходимо захватить 30° луч из самой удаленной точки дифракции, тогда ореол миграции должен равняться Z x tan30˚ = 0.58Z, как на Рис. 3.10 (в нашем примере 0,58 х 2000 м = 1160 м или 0,58 х 6500 футов = 3828 футов). Это условие определит желаемую апертуру миграции, если только понижение не превышает 30˚. В таблице 3.1 даны значения по колонкам для констант 10˚, 20˚, 30˚, т.к. критерий дифракции – это ограничивающий фактор. На практике расчеты стоимости будут зачастую влиять на желаемую апертуру. Кривые хода луча всегда буду снижать количество, необходимое для ореола миграции (Бии, 1994).

Эмпирическое правило: Ореол миграции обычно выбирается больше:

- движения латеральной миграции каждого понижения в ожидаемой геологии,

- расстояния, требуемого, чтобы уловить энергию дифракции, приходящую к поверхности под углом разветвления до 30˚ (или же похожими углами)

- и никогда не меньше радиуса первой зоны Френеля.

Таблица 3.1. Расчеты ореола миграции при большой изменяемости типичных значений

А) метрическая

Градусы→
Метры↓
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
	←Дифракция→	←Миграция понижающих событий (?)

В) стандартный (английский)

Градусы→
Футы↓
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
			∞
	←Дифракция→	←Миграция понижающих событий (?)

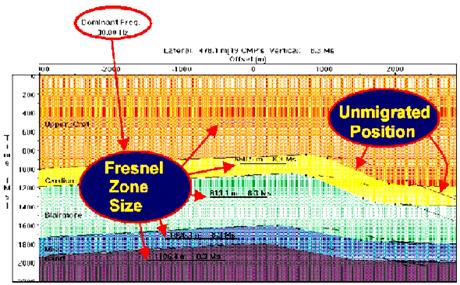
Рис. 3.11

Вывод, такой, как на Рис. 3.11, помогает определить вертикальное разрешение (четверть длины волны доминантной частоты) и латеральное разрешение перед миграцией (диаметр зоны Френеля относительно размера бина). Мы также можем использовать другие выводы, чтобы увидеть размер бина, требуемого, чтобы получить изображение желаемой высокой частоты на определенном понижении в модели. Размер съемки должен быть рассчитан, базируясь на площади, изображение которой необходимо, плюс ореол миграции.

Управление краями

Управление краями ссылается на тот аспект съемки 3D, который определяет ширину ореола миграции и уменьшение кратности.

Уменьшение кратности зависит, главным образом, от того, что считается полной кратностью. Это площадь по краю съемки, где полная кратность (или почти полная кратность) на глубине не была достигнута до миграции. Часто незначительное расслабление в определении достаточной кратности возле краев может помочь значительно снизить размер съемки.

Эмпирическое правило: Конус кратности составляет примерно 20% глубины цели (т.е. 20% от Х_мах), предполагая, что геология имеет плоскую форму. Другое приближенное значение составляет – Х_min< уменьшение кратности <2 x X_min.

Уменьшение кратности может легко добавить 30% к общей площади 3D, даже при больших съемках. На чрезвычайно маленьких съемках этот процент диспропорционально высок. Это делает съемки 3D, которые намереваются охватить всего лишь 2,5 км² (1 кв. миля) неприемлемо дорогими. Размер зоны уменьшения кратности зачастую отличается в направлении лини ПП, нежели линий ПВ, т.к. понижения могут меняться в зависимости от азимута. Следовательно, изменится и ореол миграции.

Рис. 3.12 показывает размер используемой программы (сеть уменьшения кратности) в процентном отношении к общему размеру программы, если необходимая глубина равна 2000 м (6500 футов), а ширина зоны уменьшения кратности предполагается равной 200 – 1600 м (660 – 5280 футов).

Обычно кратность набирается быстрее в направлении поперек линии, нежели вдоль. Это особенно заметно для проектов с узкими азимутами. Внимательное использование ПП может позволить набрать кратность быстрее при определенной геометрии. Ориентация заплатки относительно контура съемки может значительно повлиять на стоимость съемки.

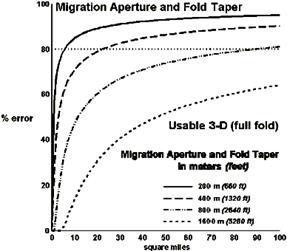
Рис. 3.12

Любая 3D съемка должна считаться состоящей из 3 зон (концентрических площадей) (Рис. 3.13).

Первая (самая внутренняя) зона – область интерпретации. Все трассы, лежащие в этой зоне, должны считаться полнократными и полномигрированными. Это область изображения, которую обработчик (интерпретатор) проверяет и использует, как основу для геологической интерпретации.

Вторая (средняя) зона – это коридор вокруг самой внутренней зоны (изображения). Теоретически ширина этого коридора равна ореолу миграции. В этом коридоре обработчик-сейсмик соберет полнократные суммированные трассы. Миграция передвинет бóльшую часть энергии этих трасс на края самой внутренней зоны (изображения).

Третья (самая удаленная) зона – это коридор вокруг средней зоны. Ширина этой зоны – уменьшение кратности (конус кратности). В этом коридоре разработчик сбора данных разместит ПП или ПВ, пытаясь гарантировать полную кратность в начале средней (полнократной) зоны.

Термин «Управление краями» перекликается с проектированием этих 3-х зон. Компромиссы могут быть сделаны, а почти всегда так и делается.

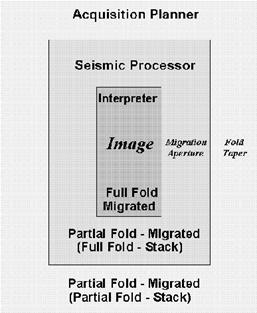
Рис. 3.13

Также возможно ослабить требование о 30° для очень больших глубин (ниже заданных) это уменьшит размер ореола миграции (размер средней зоны) (Рис.3.14).

Трассы, имеющие не совсем полную кратность, могут быть приемлемы для бинов, расположенных возле внешних краев средней зоны – они соответствуют почти 30° доли дифракции и вряд ли будут способствовать переносу большого количества энергии на края самой внутренней зоны (изображения).

Эмпирическое правило: Ни в коем случае общая зона вокруг площади изображения не должна быть менее радиуса зоны Френеля плюс размер конуса кратности.

Это означает, что полнократные трассы будут располагаться от краев области изображения к краям радиуса зоны Френеля, а к границам съемки кратность будет уменьшаться. В общем, Ореол Миграции и Уменьшение Кратности будут смешиваться, и фактор стоимости будет сильно влиять на окончательный выбор конкретного проекта.

Эксперименты с моделями и пр. в конкретном проекте помогут определить эти параметры более точно.

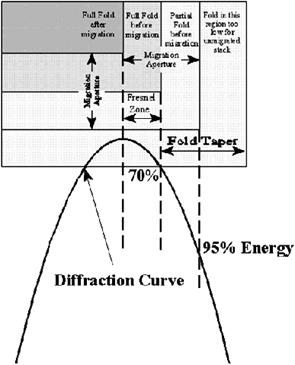
Рис. 3.14

Моделирование трассы луча

Моделирование трассы луча особенно используется, если подстилающая геология более сложная, чем модель плоских слоев, используемая для 3D проектирования. Примеры включают соляные купола, нарушения, слои с крутыми понижениями, несогласия горизонтальной скорости и многое другое. Такое моделирование может привести проектировщика к стратегиям для поверхностной расстилки, отличным от предположений при плоских слоях. Расстояния ПП/ПВ могут уменьшаться в определенных областях сейсмической съемки и все еще сохранять разрешение на структурно усложненных площадях. (Нефф, Ригдон, 1994).

Имеются изощренные компьютерные программы для оценки распределения кратности в структурных средах (напр. CENSUS с помощью 3D AIMS). С их помощью можно оценить влияние изменения распределения выносов и азимутов.

До этого времени мы говорили о точках ОСТ. В реальном мире, однако же, энергия от отражателя обычно не приходит от части того отражателя, который расположен между источником и приемником. Миграция корректирует трассы от положения их ОСТ к положению их ОГТ (Рис. 3.15). Но все же интересно узнать не только, какую кратность и прочее мы получим после миграции, но и как хорошо мы осветим каждый кусок верхушки заданной формации. Это так называемая кратность ОГТ.

Трассирование 3D луча является основным для правильного анализа ОГТ.

Рис. 3.15

Длина записи

Наконец, длина записи должна выбираться так, чтобы любые образцы дифракции до самых глубоких интересующих мест имели бы полное изображение после миграции. Включите достаточно времени так, чтобы дифракция была шириной во много трасс – так называемый ореол миграции.

Предположим, например, что существующие данные 2D показывают целевой горизонт на глубине 1,5 сек. Далее, давайте предположим, что необходимо получить изображение основания, которое расположено на глубине 2,5 сек. Хвосты дифракции расположены на уровне 500 сек, может потребоваться смещение статики до 100 мсек., а требования к аппаратуре составляют 100 – 200 мсек. Общая требуемая длина записи теперь составляет 3,3 сек; следовательно, можно вероятно выбрать 3,5 – 4 сек.

Всегда проще записать много данных, т.к. лента обычно очень дешевая в сравнении с прочими затратами на запись. Единственная загвоздка может быть с телеметрическими системами, где увеличенная длина записи может замедлить общее старание при сборе данных, т.к. возникает необходимость передать информацию с каждого пункта сразу же после того как возбуждение было предпринято.

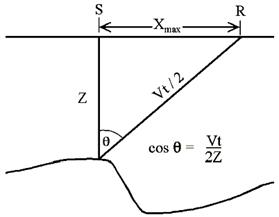
Рис. 3.16. Длина записи t, как функция рассеивания угла (Margrave, 1997).

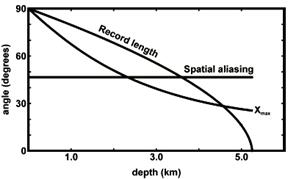
Рис. 3.17a. Постоянная скорость, рассеивающая угловой показ диаграммы: предел апертуры, рекордный предел длины, и пространственное совмещение имен ограничивают для случая когда X_max = 2500 м., t =3.0 s, V = 3500 м\с, B = 20 м., и f = 60 гц (Margrave, 1997).

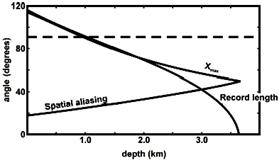
Рис. 3.17b. Постоянный градиент, рассеивающий угловой показ диаграммы: предел апертуры, рекордный предел длины, и пространственное совмещение имен ограничивают для случая когда X_max = 2500 м., t = 3.0 s, V = 1500 м\с + 0.6* Z м\с, B = 20 м., и f = 60 Гц (Margrave, 1997).

Спроектируем 3D – Часть 3

Пример со следующими известными параметрами (метрическими):

Существующие данные 2D хорошего качества кратность 30

Самые крутые понижения 30 градусов

Неглубоких горизонты, необходимые для изохрон 500 м выносы

Целевая глубина 2000 м

Двойное время пробега волны до целевого горизонта 1,5 сек

Глубина основания 3000 м

V_int над целевым горизонтом 4200 м/с

F_dom на целевом горизонте 50 Гц

F_max на целевом горизонте 70 Гц

Горизонтальный размер целевого горизонта 300 м

Предполагается прямолинейный метод!

Желаемая кратность:

½ - ²/₃ кратности 2D = 15 – 20

Размер бина:

а) для целевого размера/3 = 300 м/3 = 100 м

б) для аляйсинговой частоты

= V_int/(4 x F_max x sin (угол падения)) = 4200 м/с /(4 x 70 Гц x 30°) = 30 м

с) для латерального разрешения

= V_int/(N x F_dom x sin) = 4200 м/с /(4 x 70 Гц x 30°) = 30 м

размер бина = 30м х 30 м

интервал между ПП = 60 м

интервал между ПВ = 60 м

Х_min:

Интервал меду линиями ПП = 360 м

Интервал между линями ПВ = 360 м

X_min = (360² + 360²)^½ м = 509 м

Х_мах:

Заплатка 8 х 60 или 2520 м х 3540 м

Кол-во каналов = 480

Коэффициент сжатия = 2520/3540 = 0,71

Х_мах = ½ х (2520² + 3540²)^½ м = 2172 м

Кратность:

Кратность вдоль линии = 3600/(2 х 360) = 5

Кратность поперек линии = 8/2 = 4

Общая кратность = 20

Ореол миграции:

Радиус зоны Френеля = ½ х (целевое время х V_rms x V_int/F_dom)^½ =

Энергия дифракции = 0.58 х целевую глубину

Ореол миграции = целевая глубина х tan (понижение) =

Уменьшение кратности = 0,2 х целевую глубину =

(FT + FZ) < общий ореол миграции < (FT + MA) ООМ =