 |
Индивидуальные индексы и их свойства.
|
|
|
|
Тема 7. ИНДЕКСЫ
1) Понятие индексов
2) Индивидуальные индексы и их свойства
3) Агрегатная форма общих индексов
4) Взаимосвязь общих индексов и условия её осуществления
5) Средние формы общих индексов
6) Индексы с постоянными и переменными весами
7) Индексы качественных показателей или средних уровней
8) Системы конкретных индексов
9) Территориальные индексы
Понятие индексов.
Индекс в переводе с латинского означает указатель, показатель. Индексы относятся в обобщающим показателям и выражаются в форме коэффициента или в процентах.
Индексы в статистике – это относительные величины, характеризующие изменения уровня явления во времени, результат сопоставления изучаемого явления в пространстве, а также уровень планового задания и степень выполнения плана.
Всякая совокупность состоит из элементов, одни из которых могут быть соизмеримыми (однородные), а другие несоизмеримые (неоднородные). Внешним признаком соизмеримости является единство натуральной формы единиц и их единиц измерения. Если единицы однородной совокупности можно суммировать, то в неоднородных совокупностях непосредственного суммирования единиц произвести нельзя.
В зависимости от соизмеримости или несоизмеримости единиц совокупности, для которых исчисляются индексы, различают индивидуальные и общие индексы. Индивидуальные индексы характеризуют динамику или территориальные изменения по одному товару, одному виду продукции, одной сельскохозяйственной культуре и т.п. Для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы (изменение физического объёма продукции, включающей разноимённые товары, изменение потребительских цен и т.д.), рассчитывают общие (сводные) индексы.
|
|
|
Индексы строятся на основе различных экономических показателей, одни из которых факторные (качественные и количественные), а другие результативные.
Качественные показатели характеризуют уровень явления, т.е. рассчитываются на единицу совокупности. К этой группе показателей относятся:
p – цена единицы продукции;
z – себестоимость единицы продукции;
t – трудоёмкость единицы продукции – затраты рабочего времени на производство единицы продукции;
w – производительность труда – выработка продукции в единицу времени или на одного работающего.
Количественные показатели характеризуют объём какого-либо явления по совокупности или её части. Например:
q – физический объём товарооборота (количество проданных товаров в натуральном выражении)
s – численность работников.
Результативные показатели отражают результат взаимодействия качественно-количественных показателей. Это:
pq – товарооборот (стоимость реализованных товаров);
zq – затраты на производство продукции (себестоимость произведённой продукции);
tq – затраты рабочего времени на производство продукции (выражаются в чел/часах, чел/днях).
По базе сравнения все индексы можно разделить на две группы: динамические и территориальные. Динамические индексы отражают изменение явления во времени. Например, индекс цен на продукцию в 2007 г. по сравнению с 2006 г. При исчислении динамических индексов происходит сравнение значения показателя в отчётный период со значением этого же показателя за предыдущий период (базисный). В качестве отчётного или базисного периодов могут быть использованы плановые показатели.
Территориальные индексы применяются для межрегиональных сравнений. Большое значение эти индексы имеют в международной статистике при сопоставлении показателей социально-экономического развития различных стран.
|
|
|
С помощью экономических индексов решаются следующие задачи:
· измерение динамики социально-экономического явления за два и более периодов времени;
· измерение динамики среднего экономического показателя;
· измерение соотношения показателей по разным регионам;
· определение степени влияния изменений значений одних показателей на динамику других;
· пересчёт значений макроэкономических показателей из фактических цен в сопоставимые.
Индивидуальные индексы и их свойства.
Индивидуальные индексы рассчитываются для однородных совокупностей. Они представляют собой отношение уровня экономического явления в отчётном периоде к его уровню в базисном периоде. В общем виде этот индекс может быть записан в виде формулы:
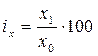 ,
,
где x – индексируемый показатель;
1,0 – принадлежность показателя к текущему (отчетному) или базисному периоду.
Индивидуальный индекс цен:
 ,
,
где  – цена товара в отчётном периоде;
– цена товара в отчётном периоде;
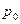 – цена товара в базисном периоде.
– цена товара в базисном периоде.
Если цена товара А в отчётном периоде составляла 55 руб. за 1 кг, а в базисном – 50 руб. за 1 кг, то индивидуальный индекс цен будет равен:
 , или 110%.
, или 110%.
Цена товара А возросла по сравнению с базисным в 1,1 раза, или на 10%.
Индивидуальный индекс физического объёма товарооборота:
 ,
,
где 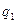 – количество проданных товаров в отчётном периоде;
– количество проданных товаров в отчётном периоде;
 – количество проданных товаров в базисном периоде.
– количество проданных товаров в базисном периоде.
Если рассматриваемого товара А в отчётном периоде продали 480 кг, а в предшествующем – 400 кг, то индивидуальный индекс физического объёма товарооборота составит:
 , или 120%.
, или 120%.
Данный индекс показывает, что физический объём продажи товара А возрос на 20%.
Индивидуальный индекс товарооборота (стоимости реализованных товаров):
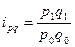 ,
,
где  и
и  – товарооборот отчётного и базисного периодов соответственно.
– товарооборот отчётного и базисного периодов соответственно.
Для нашего примера получим:
 , или 132%.
, или 132%.
Товарооборот по данному товару увеличился в текущем периоде по сравнению с базисным на 32%.
На практике часто имеются данные не за два, а за несколько последовательных периодов времени. В таких случаях строится система, состоящая из ряда индексов, характеризующих последовательное изменение изучаемого явления во времени. Различают 2 способа построения такой системы:
|
|
|
1. Индексы с постоянной базой сравнения (базисные индексы).
 .
.
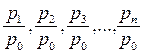 .
.
Они показывают изменение уровня явления за последовательно возрастающие периоды.
2. Индексы с переменной базой сравнения.
 .
.
Показывают, как изменяется уровень явления при переходе от одного периода к другому.
Выбор системы индексов производится в зависимости от цели анализа. Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные – чётче отражают последовательность изменения уровней во времени.
Свойства индивидуальных индексов.
1. Произведение последовательных цепных индексов равно соответственному базисному индексу:
 .
.
Это свойство позволяет вычислить базисные индексы на основе цепных.
2. Отношение каждого базисного индекса к непосредственно предшествующему базисному индексу равно цепному индексу:
 .
.
Это свойство позволяет рассчитать цепные индексы на основе базисных.
3. Индекс произведения двух или более сомножителей равен произведению индексов этих сомножителей.
Если товарооборот равен произведению цены товара на количество проданных товаров, то  .
.
 .
.
|
|
|


