 |
Индексы качественных показателей или средних уровней.
|
|
|
|
Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в пределах одной территории, или нескольким видам продукции, производимым на одном предприятии. Рассмотрим случай, когда один товар реализуется в нескольких местах или один вид продукции производится на ряде предприятий.
При изучении динамики качественных показателей приходятся определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов – изменением значения индексируемого показателя у отдельных групп единиц и изменением структуры явления. Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности. Например, средняя заработная плата на предприятии может вырасти в результате роста оплаты труда работников или увеличения доли высокооплачиваемых сотрудников.
В связи с этим возникает задача определить степень влияния каждого из факторов на общую динамику среднего значения. Эта задача решается индексным методом путём построения системы взаимосвязанных индексов, в которую включают 3 индекса: переменного состава, постоянного состава и структурных сдвигов.
В общем виде индекс переменного состава – это отношение средней величины качественного показателя в отчётном периоде к средней его величине в базисном периоде.
Индекс может быть записан в двух формах:
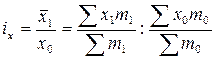 или
или 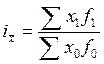 ,
,
где 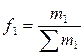 и
и 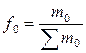 – доли отдельных частей совокупности в её общем объёме соответственно в отчётном и базисном периодах.
– доли отдельных частей совокупности в её общем объёме соответственно в отчётном и базисном периодах.
Индекс переменного состава показывает изменение средней величины показателя 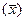 за счёт совместного влияния двух факторов:
за счёт совместного влияния двух факторов:
1. изменение уровня индексируемого показателя в отдельных частях совокупности 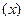 ;
;
|
|
|
2. изменения частей совокупности 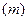 или доли этих частей совокупности
или доли этих частей совокупности  , т.е. изменение структуры совокупности, структурных сдвигов.
, т.е. изменение структуры совокупности, структурных сдвигов.
Разность между числителем и знаменателем индекса
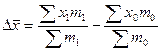
показывает абсолютное изменение средней величины изучаемого показателя за счёт совместного влияния двух факторов.
Для того, чтобы охарактеризовать изменение средней величины показателя за счёт каждого фактора в отдельности, нужно поочерёдно устранить влияние одного из факторов, зафиксировав его на постоянном уровне. Эта задача решается с помощью индексов постоянного состава и структурных сдвигов.
Индекс постоянного состава:
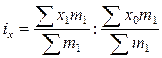 или
или 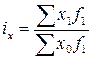 .
.
В этом индексе устраняется влияние m или f, т.е. второго фактора (изменение частей совокупности или структуры совокупности), и оценивается влияние изменения x – первого фактора (изменение уровня индексируемого показателя).
Индекс постоянного состава показывает изменение средней величины показателя только за счёт изменения уровня показателя в отдельных частях совокупности.
Разность между числителем и знаменателем индекса

показывает абсолютное изменение средней величины изучаемого показателя за счёт изменения уровня показателей в отдельных частях совокупности.
Индекс структурных сдвигов:
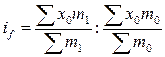 или
или 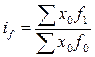 .
.
Индекс структурных сдвигов устраняет влияние x и оценивает влияние изменения m или f – второго фактора.
Индекс структурных сдвигов показывает, как изменилась средняя величина показателя за счёт изменения структуры совокупности.
Разность между числителем и знаменателем индекса

показывает абсолютное изменение средней величины изучаемого показателя за счёт изменения структуры совокупности.
Взаимосвязь: произведение индексов постоянного состава и структурных сдвигов равно индексу переменного состава: 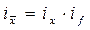 .
.
Абсолютное изменение равно 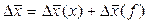 .
.
|
|
|
|
|
|


