 |
Удаление математических выражений
|
|
|
|
Удаление отдельных символов осуществляется с помощью клавиш «Backspace» (Бекспейс) (←). При этом визир следует ставить после удаляемого символа.
Удаление одного математического выражения, например уравнения, осуществляется следующим образом.
Сначала следует с помощью левой клавиши мыши очертить это выражение пунктирной линией, которая затем превращается в сплошную линию (после снятия пальца с клавиши).
Затем необходимо нажать на клавишу «Backspace» (←), после чего все нажатие будет выделено (затемнено) и вновь нажать на клавишу «Backspace» (←) или «Del».
Выделение удаляемого выражения можно также осуществить путем протаскивания вдоль него курсора, после чего следует нажать на клавишу «Backspace» (←) или «Del».
Одновременное удаление двух и более математических выражений можно осуществить следующим образом.
Сначала следует с помощью левой клавиши мыши очертить всю удаляемую группу выражений пунктирной линией, после чего каждое из удаляемых выражений будет окружено пунктирной линией.
Следующее действие может быть осуществлено одним из трех способов:
· путем нажатия на клавишу «Backspace» (←) или «Del»;
· или путем обращения к команде «Вырезать» на стандартной линейке или «Удалить» в меню «Правка»;
· или нажатием на правую клавишу «мыши», после чего появляется дополнительное окно, в котором есть строка «Вырезать».
Копирование математических выражений
Сначала необходимо с помощью левой клавиши мыши очертить всю копируемую группу выражений пунктирной линией, после чего каждое из них будет окружено пунктирной линией.
Второе действие может быть осуществлено одним из двух способов:
1. путем обращения к команде «Копировать» на стандартной линейке или в меню «Правка»;
|
|
|
2. нажатием на правую кнопку клавиши мыши, после чего появляется дополнительное окно, в котором есть опция «Копировать».
При копировании отдельного выражения первое из названных действий (выделение) можно осуществить протаскиванием курсора вдоль копируемого выражения, после чего следует выполнить команду «Копировать».
После выполнения команды «Копировать» выражение хранится в буфере обмена.
Перенос математических выражений
1-й вариант: аналогичен копированию выражений, но после выполнения опции «Копировать» необходимо выполнить команду «Вставить» на стандартной линейке или из дополнительного окна после нажатия на правую клавишу мыши, место вставки следует указать курсором.
2-й вариант: необходимо с помощью левой клавиши мыши очертить всю копируемую группу выражений пунктирной линий, после чего каждое из них будет окружено пунктирной линией.
Затем подвести курсор-стрелку к любой из пунктирных линий и дожидаться преобразования курсора в изображение кисти руки.
Далее, не снимая пальца с левой клавиши мыши, следует перетянуть всю группу выражений в требуемое место рабочей области.
При перетягивании курсор примет вид стрелки с прямоугольником.
Вписывание в программу текстовых комментариев
Данная операция осуществляется под руководством текстового редактора.
После ввода с клавиатуры символа “ (кавычки) в месте нахождения красного визира появится прямоугольник, в который и вводится требуемый текст в полном соответствии с правилами работы редактора «Word».
Редактирование введенного текста может быть осуществлено с помощью подменю «Текст» меню «Формат» и опций, вынесенных на линейку «Форматирование».
Удаление, копирование и перенос текстовых комментариев осуществляется по той же методике, что и математических выражении.
|
|
|
Правила вычислений в среде «MathCAD»
Возможны два типа вычислений в среде MathCAD, осуществляемые с помощью формульного редактора:
· численный;
· символьный.
При первом типе результат получается в виде числа, при втором – в форме математического выражения.
Реализация численного способа осуществляется:
1. путем обращения к панелям математических инструментов из меню «Вид» (View);
2. путем обращения к встроенным функциям f(x) из меню «Вставка» (Insert);
3. с помощью клавиатуры.
Реализация символьного способа, при котором происходит преобразование одного математического выражения в другое, осуществляется:
1. путем обращения к меню «Символы» (Symbolics);
2. путем обращения к панели математических инструментов «Символы» из меню «Вид»;
3. с помощью клавиатуры.
Запись математических выражений в составляемую программу осуществляется с помощью:
1. математических инструментальных панелей;
2. путем обращения к встроенным функциям f(x);
3. с помощью клавиатуры.
В том месте рабочей области текстового окна, где установлен курсор – стрелка, после щелчка левой клавиши «Мыши» возникает визир в форме значка + красного цвета.
На месте установки визира отражается результат той или иной команды или операции и происходит ввод в программу требуемого математического выражения.
После ввода первого символа визир преобразуется в две линии – горизонтальную и вертикальную – синего цвета.
Перемещение визира осуществляется с помощью мыши при нажатой клавише или клавиш клавиатуры, ответственных за перемещение курсора.
Правила численного и символьного методов решения математических задач в среде «MathCAD»
Правило 1 – связано с обращением к панелям математических инструментов из меню «Вид»: «Арифметика», «Матрицы» и «Математический анализ» или «Исчисления».
Оно позволит получить результат в виде числа.
Сначала щелчком вызывается соответствующая панель инструментов, а затем производится щелчок по требуемой пиктограмме (кнопке), после чего в рабочей области текстового окна в месте установки красного визира появляется определенное выражение. Вписывание в него исходных данных и ввод знака равенства дает числовой результат.
|
|
|
Примеры
1. Вычислить косинус угла, равного 0,5 радиана.
Вызываем панель «Арифметика», щелчок по кнопке «cos». В рабочей области текстового окна появляется выражение:
 cos ()
cos ()
Вписывается внутрь скобок число 0,5 – получаем:
cos (0.5)
Вводим знак (=), после чего автоматически получаем результат:
cos (0.5) = 0.878
В меню математика должен стоять автоматический расчет (либо щелкнуть «вычисление») (автоматическое вычисление).
2. Вычислить определенный интеграл от функции sin2(x) в пределах изменения аргумента от 0,5 до 2.
Вызываем панель «Матанализ» («Исчисления»), щелчок по пиктограмме, на которой изображен определенный интеграл.
В рабочей области текстового окна в месте установки красного визира появляется выражение:

Вписываем в него значения верхнего и нижнего пределов интегрирования, а под знаком интеграла заданную функцию, вводим знак =, после чего автоматически получаем результат:

3. Получить из заданной матрицы размером 3х3 транспонированную матрицу.
Вызываем панель инструментов «Матрица» (меню «Вид» → подменю математика).
На ней делаем щелчок по пиктограмме, на которой изображена матрица.
В рабочей области текстового окна в месте установки красного визира появляется диалоговое окно, в котором после слов «строки» и «столбцы» вписываем заданные числа: 3 и 3.
После нажатия на кнопку «ОК» или «Вставить» в тексте программы появляется матрица выбранной размерности. Вписываем в ячейки матрицы требуемые числа.
Обрамляем с помощью курсора всю запись пунктирной линией и щелкаем по пиктограмме MТ, означающей выполнение операции по транспонированию матрицы.
Вводим знак равенства, после чего автоматически получаем результат:

Вызов матрицы можно также произвести путем обращения к подменю «Матрица» из меню «Вставка».
Правило 2 – связанное с обращением к встроенным функциям f(x) из меню «Вставка», либо к пиктограмме «Встроенная функция f(x)» на 2-ой строке текстового окна – стандартной линейке.
Результат будет получен в виде числа. На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбирается определенное имя, тип функции, а в разделе «Название функции» - требуемая функция
|
|
|
После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна появляется выбранная функция, в которую вписываются заданные числа, и вводится знак «=», после чего автоматически получается результат.
Пример
Вычислить функцию Бесселя 1-ого рода 1-ого порядка при аргументе 5.
Обращаемся к пиктограмме встроенная функция f(x) на 2-ой строке текстового окна – стандартной линейке.
На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Бесселя», а в разделе» Название функций» - I 1.
После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна в месте установки красного визира появляется выражение I 1 (■).
Вписываем внутрь скобок заданное значение аргумента – I 1 (5) – и вводим знак =, после чего автоматически получаем результат: I 1 (5) = 24.336
Правило 3
Это правило связано с вводом необходимых знаков с помощью клавиатуры. Оно позволяет получить результат, как в численном виде, так и в символьном виде.
Данное правило, по существу, аналогично двум предыдущим.
Только здесь все знаки – числа, арифметические действия и латинские обозначения – вводятся в текст составляемой программы с помощью клавиатуры.
Возможен ввод и специальных операторов при символьных вычислениях путем одновременного нажатия двух или трех клавиш.
Рассмотрим некоторые примеры по вводу специальных знаков:
1. для ввода оператора 1-ой производной следует одновременно нажать на две клавиши: shift+?;
2. для ввода оператора n-ой производной следует одновременно нажать при клавиши: ctrl+shift+?;
3. для ввода знака неопределенного интеграла следует нажать на две клавиши: ctrl+I;
4. для ввода знака определенного интеграла следует нажать две клавиши: shift+&;
5. исполнение символьных операций дифференцирования и интегрирования осуществляется нажатием двух клавиш: shift+F9;
Правило 4
Оно связано с обращением к математической панели инструментов «Символы» (в меню «Вид» →Панели инструментов→Символы) и позволяет получить результат как в символьном, так и численном виде.
1. Математическое выражение, подлежащее преобразованию, записывается в рабочей области текстового окна и с помощью курсора обрамляется рамкой.
2. Далее в зависимости от вида преобразования выбирается соответствующее ключевое слово:
· Ряд – при разложении функции в степенной ряд Маклорена по выбранной переменной;
|
|
|
· Расширить – при разложении в степенной ряд выражений типа бинома Ньютона;
· Комплекс – при преобразовании комплексных чисел;
· Mт→, M-1→, |М|→, - при транспонировании, обращении (инвертировании) матриц и расчете их определителя;
· Символьный знак равенства → - при дифференцировании и т.д.
1. После щелчка по выбранному ключевому слову к записи автоматически добавляется это слово и символический знак равенства →.
2. После второго щелчка вне рамки записи автоматически появляется результат в виде нового символьного выражения, полученного из исходного в результате преобразования.
Примеры
1 
2 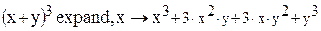
3 
4 
5 
6 
Правило 5
Правило связано с обращением к меню «Символы», подменю «расчеты». Оно позволяет произвести символьные вычисления, в том числе и в комплексной области.
Математические выражения, связанные между собой определенными операциями, записываются в рабочей области текстового окна, и с помощью курсора обрамляются рамкой.
Далее щелчком производится обращение к строке «символические» при дифференцировании функций и других операциях, а при работе с комплексными выражениями – к строке «комплексные».
После щелчка на рабочем столе появляется результат в виде нового выражения, располагаемого под исходной записью.
Примеры
1. 

Используется подменю «Расчеты», опция «символические»
2. 

Используется подменю «Расширить»
3. 

4. 

Используется опция «Символические»
Правило 6
Оно также связано с обращением к меню «Символы».
Позволяет произвести разнообразные символьные преобразования, записав в рабочей области текстового окна подлежащее преобразованию выражение.
При обращении к подменю «Переменные» в этом выражении необходимо выделить (затемнить ■) один символ – переменную – путем протаскивания курсора.
Далее с помощью подменю «Переменные» можно выполнить следующие операции:
· найти корни алгебраического и трансцендентного уравнений (опция «Вычислить»);
· произвести дифференцирование функции (строка «Дифференциалы»);
· произвести интегрирование функции (строка «Интеграция»);
· разложить функцию в степенной ряд Маклорена (строка «Преобразовать в частичные доли»).
При обращении к подменю «Матрица» следует обрамить рамкой все выражение. Это подменю позволяет осуществить транспонирование и обращение (инвертирование) матрицы и найти ее определитель.
При обращении к подменю «Преобразования» можно произвести прямое и обратное преобразования: Фурье, Лапласа и типа Z.
Построение графиков в составляемой программе на основе исходных данных или результатов вычислений осуществляется в среде MathCAD под руководством графического редактора.
При построении графиков можно воспользоваться инструментальной панелью «График» из меню «Вид» или подменю «График» в меню «Вставка».
С их помощью можно построить двухмерные графики в декартовой и полярной системе координат, трехмерные и точечные графики, векторное поле и гистограммы.
Рассмотрим сначала на конкретном примере методику построения двухмерного графика в декартовой системе координат.
|
|
|


